
|
|
Нормы плавности работы, мкм12 Методическое руководство к лабораторной работе для студентов заочных отделений приборостроительных Специальностей
Казань – 2006 УДК 531.8 (076.5) Настоящее методическое руководство составлено в соот-ветствии с программой учебной дисциплины «Прикладная механика» и предназначено для студентов заочных отделений приборостроительных специальностей КГТУ им. А.Н. Туполева. В руководстве даны описание и порядок выполнения лабораторной работы по основам зубчатого зацепления, рассмотрены общее устройство и характеристики используемых измерительных приборов. Кроме того, приведены необходимые справочные данные. Методическое руководство составлено к.т.н., доцентом Сачковым А.В., к.т.н., доцентом Печенкиным В.М., к.т.н., доцентом Якуповой И.П., к.т.н. Карбовским В.А., Морозовой А.С.
Рецензенты: д.ф.-м.н., профессор Иванов В.А. (КГТУ им. С.М. Кирова) к.т.н., доцент Мудров А.П. (ГСХА, г. Казань)
Лабораторная работа
ИССЛЕДОВАНИЕ ГЕОМЕТРИИ И ТОЧНОСТИ ЦИЛИНДРИЧЕСКОЙ ЗУБЧАТОЙ ПРЕДАЧИ
1.Цель работы Целью работы является: определение геометрических параметров эволь-вентной цилиндрической зубчатой передачи; определение параметров точности передачи; составление рабочего чертежа заданного зубчатого колеса.
2.Основные сведения о параметрах цилиндрической зубчатой передачи
Зубчатая передача – это механизм, который с помощью зацепления передает или преобразует движение с изменением угловых скоростей и моментов. Зубчатые передачи между параллельными валами осуществляются цилин-дрическими колесами с прямыми, косыми и шевронными зубьями (рис.1). Эти передачи называют цилиндрическими.

Рис.1 Существуют передачи внешнего зацепления (рис.1,а – в) (прямозубые, косо-зубые, шевронные) и передачи внутреннего зацепления (рис.1,г). Достоинства зубчатых передач: малые габариты, высокий КПД, высокая надежность в работе, постоянство передаточного отношения, возможность применения в широком диапазоне моментов, скоростей и передаточных отно-шений. Недостатки: требование высокой точности изготовления, шум в работе со значительными скоростями. Шум обусловлен, в основном, ошибками изготов-ления шага, профиля зубьев, а также переменной жесткостью зацепления и под-шипниковых опор вала. Зубчатая передача состоит из двух зубчатых колес с числами зубьев Зацепление зубчатых колес эквивалентно качению без скольжения окруж-ностей с диаметрами
Рис.2 Эти окружности называются начальными. Точка их касания
Основное кинематическое условие, которому должны удовлетворять про-фили зубьев передачи – это постоянство передаточного отношения Наибольшее распространение получило эвольвентное зацепление из-за преи-муществ перед другими (для нарезания применяется простой инструмент, воз-можно применение одного и того же инструмента независимо от числа зубьев). Эвольвенты профилей образуются точками К прямой N1N2 при качении ее без скольжения по окружностям с диаметрами Линия N1N2 перемещения общей точки контакта К профилей зубьев при вращении колес называется линией зацепления. Угол Линия зацепления всегда является касательной к основным окружностям При увеличении диаметров основных окружностей радиусы кривизны эвольвент N1К и N2К увеличиваются. В пределе эвольвента превращается в прямую линию, а зубчатый венец – в рейку с трапециевидным профилем зуба. Такая рейка называется исходной. Исходный контур (ИК) – контур зубчатой рейки с трапециевидным профилем зубьев. ИК характеризует параметры любого эвольвентного зубчатого венца (рис.3,a).
Рис.3 а – ИК колеса; б – исходный производящий контур (ИПК). Исходный производящий контур (ИПК) – контур зубьев зубчатой рейки, ха-рактеризующий параметры зуборезного инструмента и отличающийся от ИК только высотой зубьев на величину радиального зазора Исходный контур имеет линию впадин зубьев Шаг зубьев Зубчатое колесо имеет окружность впадин ( Окружной делительный шаг зубьев колеса
 , мм. (1) , мм. (1)

Рис.4 Параметры исходного контура стандартизованы и задаются в долях модуля. Для передач с модулем В высоконапряженных авиационных зубчатых передачах применяют ИПК с Нарезание зубьев колес осуществляется реечным инструментом (червячной фрезой) или долбяком методом огибания. При реечном инструменте кинемати-ческая цепь зуборезного станка настраивается так, чтобы начальная прямая рейки катилась без скольжения по делительной окружности нарезаемого колеса (рис.4). NК - линия зацепления при нарезании зубьев, К - режущая точка в данный момент времени. Начальная прямая – делительная прямая
Рис.5 В косозубом колесе ось зуба имеет наклон по отношению к боковой цилин-дрической поверхности колеса (основному цилиндру диаметром
Рис.6 Основной угол наклона зубьев При известных модуле 1.Для колес без смещения (
2.Для колес, нарезанных с положительным смещением (
угол
С учетом приведенных выше соотношений диаметр окружности вершин
радиусы начальных окружностей межосевое расстояние коэффициент воспринимаемого смещения
С учетом воспринимаемого смещения
Тогда Толщина зуба зубчатого колеса по делительной окружности может быть определена по формуле
Коэффициент перекрытия определяется по формуле
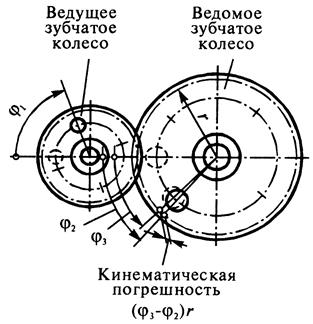
Точность зубчатых передач. Погрешности изготовления зубчатых колес приводят к повышению динамических нагрузок, вибрации, шуму передач. На-рушается мгновенное передаточное отношение и согласованность вращения ве-дущего Основными погрешностями изготовления и монтажа зубчатых колес явля-ются погрешности окружного шага, формы профиля и направления зубьев. Показатели точности (допуски) цилиндрических зубчатых передач и колес регламентируются ГОСТами. Установлено 12 степеней точности зубчатых ко-лес и передач, обозначаемых в порядке убывания точности цифрами 1, 2, 3, …, 12. Наиболее распространенными в машиностроении степени точности в бы-строходных передачах ( Для каждой степени точности ГОСТ 1643-81 (для колес с Нормы кинематической точности определяются требованиями к параметрам колеса, обеспечивающими минимальное отклонение передаточного отношения передачи. Различают кинематическую точность зубчатой передачи и зубчатого колеса. Кинематическая точность передачи характеризуется полной погрешностью углов поворота сцепляющихся колес за один оборот и равна разности между действительным и номинальным (расчетным) углами поворота ведомого зубчатого колеса передачи. Выражается в линейных величинах длиной дуги его делительной окружности (рис.7). Наибольшую алгебраическую разность значений кинематической погреш-ности передачи за полный цикл изменения относительного положения зуб-чатых колес (т.е. в пределах числа оборотов большего зубчатого колеса, рав-ному частному от деления числа зубьев меньшего зубчатого колеса на общий наибольший делитель чисел зубьев обоих зубчатых колес передачи) (рис.8) называют наибольшей кинематической погрешностью передачи
Рис.7
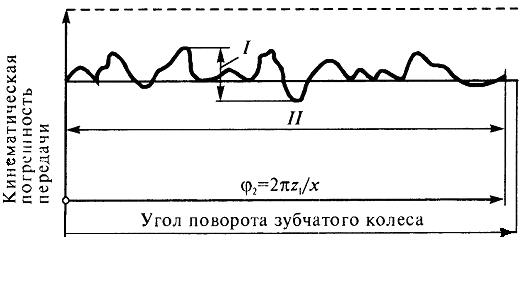
Кинематической погрешностью зубчатого колеса называют разность между действительным и номинальным (расчетным) углами поворота зубчатого коле-са на его рабочей оси, ведомого измерительным зубчатым колесом при номи-нальном взаимном положении осей вращения этих колес. Под измерительным зубчатым колесом понимается зубчатое колесо повышенной точности, приме-няемое в качестве измерительного элемента для контроля зубчатых колес. Наибольшую алгебраическую разность значений кинематической погреш-ности зубчатого колеса в пределах его полного оборота называют наибольшей кинематической погрешностью зубчатого колеса Допуск на кинематическую погрешность зубчатого колеса обозначают
 
Рис.10 Разность между наибольшей и наименьшей действительными длинами об-щей нормали в одном и том же зубчатом колесе называется колебанием длины общей нормали Отклонением шага fPtr называют дискретное значение кинематической по-грешности зубчатого колеса при его повороте на один номинальный угловой шаг (см. рис.9 при Разность между действительным и номинальным шагами зацепления (рис.11) называется отклонением шага зацепления fPbr.
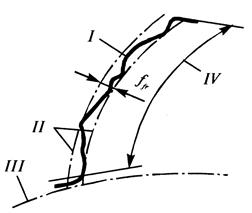
Рис.11 При этом под действительным шагом зацепления понимается кратчайшее расстояние между двумя параллельными плоскостями, касательными к двум одноименным активным боковым поверхностям соседних зубьев зубчатого колеса. Предельные отклонения шага зацепления: верхнее - +fPb, нижнее - -fPb. Погрешность профиля зуба ffr - это расстояние по нормали между двумя ближайшими друг к другу номинальными торцовыми профилями зуба, между которыми размещается действительный торцовый активный профиль зубчатого колеса (рис.12).
Рис.12 Под действительным торцовым профилем зуба понимается линия пересечения действительной боковой поверхности зуба зубчатого колеса в плоскости, перпендикулярной его рабочей оси. Допуск на погрешность профиля зуба обозначается ff. Часть активной боковой поверхности зуба зубчатого колеса, на которой рас-полагаются следы прилегания зубьев парного зубчатого колеса в собранной пе-редаче после вращения под нагрузкой, устанавливаемой конструктором, назы-вается суммарным пятном контакта. Нормы контакта зубьев определяются величинами пятен контакта сопряженных зубьев в передаче (например, при контроле «на краску») и оцениваются в % как по длине зуба [(

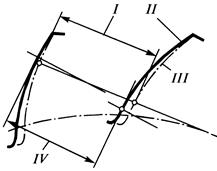
Погрешностью направления зуба Fbr называют расстояние между двумя ближайшими друг к другу номинальными делительными линиями зуба в торцовом сечении, между которыми размещается действительная делительная делительная линия зуба, соответствующая рабочей ширине зубчатого венца или полушеврона (рис.14).
Рис.14 На рисунке обозначены: I - действительная делительная линия зуба; II - но-минальные делительные линии зуба; III - ширина зубчатого венца; IV- рабо-чая ось зубчатого колеса. Под действительной делительной линией зуба пони-мается линия пересечения действительной боковой поверхности зуба зубчатого колеса делительным цилиндром, ось которого совпадает с рабочей осью. До-пуск на направление зуба обозначается Fb. Отклонением от параллельности осей fxr называют отклонение от парал-лельности проекций рабочих осей зубчатых колес в передаче на плоскость, в которой лежит одна из осей и точка второй оси в средней плоскости передачи (рис.15). fxr определяется в торцовой плоскости в линейных единицах на длине, рав-ной рабочей ширине зубчатого венца или ширине полушеврона. Допуск парал-лельности осей обозначается fx, а под средней плоскостью передачи понимается плоскость, проходящая через середину рабочей ширины зубчатого венца. Перекосом осей fyr называют отклонение от параллельности проекций рабочих осей зубчатых колес в передаче на плоскость, перпендикулярную но-минальным положениям осей, проходящую через одну из осей и перпен-дикулярную плоскости, в которой лежит эта ось и точка второй оси в средней плоскости передачи. Перекос осей определяется в торцовой плоскости в линейных единицах на длине, равной рабочей ширине зубчатого венца или полуширине шеврона (Рис.15). Допуск на перекос осей обозначается fy.
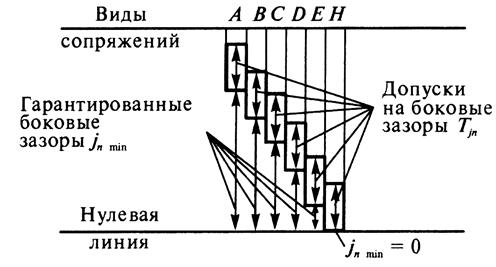
Рис.15 Отклонением межосевого расстояния far называют разность между действи-тельным и номинальным межосевыми расстояниями в средней торцовой плоскости передачи. Предельные отклонения межосевого расстояния - ± fa. Допускается комбинирование норм кинематической точности, норм плав-ности работы и норм контакта зубьев зубчатых колес и передач разных сте-пеней точности. При этом нормы плавности работы мелкомодульных зубчатых колес и передач могут быть не более чем на одну степень точнее или грубее норм кинематической точности, для колес с Кроме степеней точности для зубчатых колес и передач установлены виды сопряжения (рис.16), обозначаемые прописными буквами латинского алфавита (А, B, C, …), и виды допусков на боковые зазоры ( Вид сопряжения характеризует гарантированный боковой зазор Для зубчатых колес с
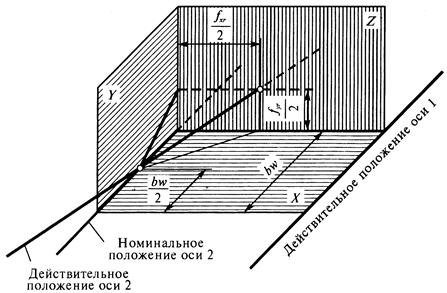
Рис.16 Сопряжение вида В обеспечивает номинальное значение бокового зазора, при котором исключается возможность заклинивания стальной или чугунной передачи от нагрева при разности температур зубчатых колес и корпуса в 250С. Видам сопряжений H и E соответствует вид допуска на боковой зазор Для зубчатых колес с Для нерегулируемых мелкомодульных передач установлено пять классов от-клонений межосевого расстояния, обозначаемых в порядке точности римскими цифрами от II до VI, для передач с Гарантированный боковой зазор в каждом сопряжении обеспечивается при соблюдении предусмотренных классов отклонений межосевого расстояния. В передачах с Виды сопряжений зубчатых колес в зависимости от степени точности по нормам плавности работы приведены в табл.П.2.12 и табл.П.3.12. Допускается изменять соответствие между видом сопряжения и классом отклонений межосевого расстояния. Точность изготовления зубчатых колес и передач задается степенью точ-ности, а требования к боковому зазору – видом сопряжения по нормам боково-го зазора. С целью обеспечения в передаче гарантированного бокового зазора при из-готовлении зубчатого колеса осуществляется дополнительное смещение исход-ного контура от его положения в теле зубчатого (червячного) колеса, обознача-емое ЕHr(рис.17).
Рис.17 На рисунке обозначены: 1 - номинальное положение исходного контура; 2 - действительное положение исходного контура. Наименьшее дополнительное смещение исходного контура, обозначаемое для зубчатого колеса с внешними зубьями - ЕHs, с внутренними зубьями - + ЕHi, это наименьшее предписанное смещение элемента исходного контура (оди-ночного зуба или впадины), условно наложенного на профиль зубьев зубчатого колеса, осуществляемое с целью обеспечения в передаче гарантированного бокового зазора. Допуск на дополнительное смещение исходного контура обоз-начается ТН.
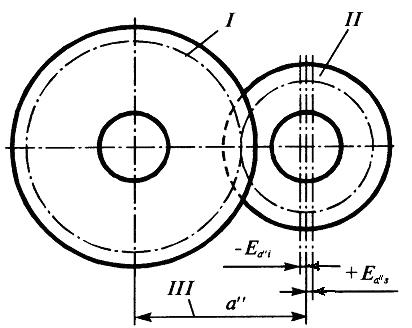
Рис.18 Предельным отклонением измерительного межосевого расстояния называет-ся разность между допускаемыми наибольшими или соответственно наимень-шими измерительным и номинальным межосевыми расстояниями (рис.18). На рисунке обозначены: I - контролируемое зубчатое колесо; II - изме-рительное зубчатое колесо; III - номинальное измерительное межосевое рас-стояние. Предельные отклонения измерительного межосевого расстояния обознача-ют: - для зубчатых колес с внешними зубьями: верхнее + -для зубчатых колес с внутренними зубьями: верхнее - Для обеспечения гарантированного бокового зазора в передаче вместо до-полнительного смещения исходного контура нормируется наименьшее откло-нение средней длины общей нормали

Отклонение средней длины общей нормали (разность значений средней нор-мали по зубчатому колесу и номинальной длины общей нормали) обозначается Номинальная длина общей нормали обозначается Номинальная толщина зуба (по постоянной хорде) Параметры

Измерение размеров по роликам у прямозубых колес позволяет контро-лировать толщину зуба точнее, чем при измерении другими способами. Осо-бенно это относится к контролю мелкомодульных колес. Размер по роликам для колеса с внешними зубьями может быть вычислен по формулам: для колеса с четным числом зубьев
где
здесь
для колеса с нечетным числом зубьев Разность действительной и номинальной величинами размера
где
При этом величина
Величины Вводится также эффективный коэффициент осевого перекрытия передачи Условные обозначения точности зубчатых колес и передач. Если все нормы назначены по одной степени точности, то обозначение про-изводится одной цифрой и одной буквой, например: 7-С ГОСТ 1643-81 - сте-пень точности 7, по всем нормам (кинематической точности, плавности работы и контакта зубьев) вид сопряжения - При комбинировании норм из разных степеней точности и изменении соот-ветствия между видом сопряжения и видом допуска на боковой зазор, но при сохранении соответствия между видом сопряжения и классом отклонений меж-осевого расстояния, точность зубчатых колес и передач обозначается последо-вательным написанием трех цифр и двух букв. Первая цифра обозначает сте-пень по нормам кинематической точности, вторая - степень по нормам плав-ности работы, третья – по нормам контакта зубьев, первая из букв – вид сопря-жения, а вторая – вид допуска на боковой зазор. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и
и  , расположенных на валах. Основными характеристиками передачи являются мощности на валах Р1 и Р2, угловые скорости
, расположенных на валах. Основными характеристиками передачи являются мощности на валах Р1 и Р2, угловые скорости  и
и  , окружная скорость на делительном цилиндре
, окружная скорость на делительном цилиндре  в м/с, КПД.
в м/с, КПД. и
и 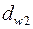 (рис.2).
(рис.2).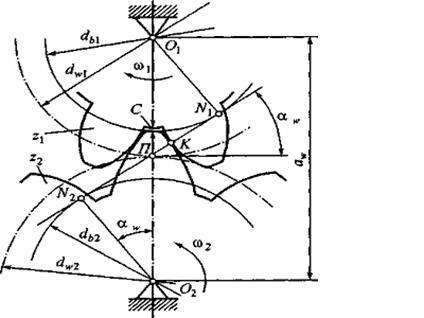
 называется полюсом зацепления. Полюс лежит на линии, соединяющей оси колес О1 и О2. Расстояние между осями колес
называется полюсом зацепления. Полюс лежит на линии, соединяющей оси колес О1 и О2. Расстояние между осями колес  называется начальным межосевым расстоянием. Оно может быть вычислено по формуле
называется начальным межосевым расстоянием. Оно может быть вычислено по формуле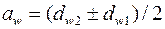 , где знак “-“ - для внутреннего зацепления.
, где знак “-“ - для внутреннего зацепления. . При этом нормаль N1N2 к профилям зубьев в точке контакта К должна проходить через полюс зацепления. Этому условию удовлетворяют многие классы кривых (эвольвента, циклоида и др.).
. При этом нормаль N1N2 к профилям зубьев в точке контакта К должна проходить через полюс зацепления. Этому условию удовлетворяют многие классы кривых (эвольвента, циклоида и др.). или
или  (см. рис.2). Эти окружности называются основными.
(см. рис.2). Эти окружности называются основными. между линией зацепления и прямой, перпендикулярной межосевой линии, называется углом зацепления.
между линией зацепления и прямой, перпендикулярной межосевой линии, называется углом зацепления. и
и 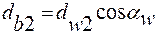 . При изменении межосевого расстояния, например, из-за ошибок изготовления, вместе с осями колес пере-местятся и основные окружности. При этом изменятся угол зацепления, диаметры начальных окружностей. Эвольвенты будут касаться другими участками, не нарушая закона зацепления, что является преимуществом эвольвентного зацепления.
. При изменении межосевого расстояния, например, из-за ошибок изготовления, вместе с осями колес пере-местятся и основные окружности. При этом изменятся угол зацепления, диаметры начальных окружностей. Эвольвенты будут касаться другими участками, не нарушая закона зацепления, что является преимуществом эвольвентного зацепления.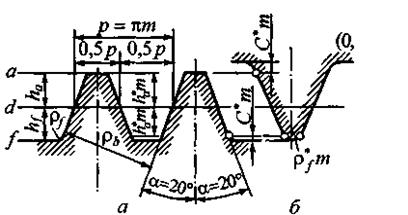
 (см. рис.3,б).
(см. рис.3,б). , линию вершин зубьев
, линию вершин зубьев  , делительную линию
, делительную линию  . Зуб включает головку
. Зуб включает головку  и ножку
и ножку  .
. расстояние между одноименными профилями соседних зубьев. Основной шаг
расстояние между одноименными профилями соседних зубьев. Основной шаг  . На делительной линии ИК толщина зуба равна половине шага (толщина зуба равна ширине впадины).
. На делительной линии ИК толщина зуба равна половине шага (толщина зуба равна ширине впадины). ), окружность вершин (
), окружность вершин (  ), делительную окружность (
), делительную окружность (  измеряется по дуге делительной окружности и равен шагу ИК. При нарезании зубчатого колеса на делительной окружности откладывается целое число шагов, равное числу зубьев. Диаметр делительной окружности находится из равенства
измеряется по дуге делительной окружности и равен шагу ИК. При нарезании зубчатого колеса на делительной окружности откладывается целое число шагов, равное числу зубьев. Диаметр делительной окружности находится из равенства 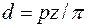 . Так как
. Так как  число иррациональное, его заменили числом
число иррациональное, его заменили числом  - моду-лем зацепления. Модули стандартизованы в диапазоне 0,05 …100 мм (ГОСТ 9563-80). При известной высоте зуба
- моду-лем зацепления. Модули стандартизованы в диапазоне 0,05 …100 мм (ГОСТ 9563-80). При известной высоте зуба 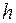 модуль может быть определен по формуле
модуль может быть определен по формуле


 =1…100 мм по ГОСТ 13755-81 угол профиля
=1…100 мм по ГОСТ 13755-81 угол профиля 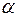 =200. Коэффициенты высоты головки и ножки зуба
=200. Коэффициенты высоты головки и ножки зуба  =1, радиального зазора
=1, радиального зазора  =0,25, радиус скругления
=0,25, радиус скругления  =0,38. Для мелкомодульных передач
=0,38. Для мелкомодульных передач  , где
, где  коэффициент смещения ИК (см. рис.4,б). Положительным принято смещение от центра колеса (+
коэффициент смещения ИК (см. рис.4,б). Положительным принято смещение от центра колеса (+ 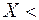 0) и малом числе зубьев возможно их подрезание, т.е. срезание части эвольвенты вблизи основной окружности, что снижает несущую способность передачи (рис.5).
0) и малом числе зубьев возможно их подрезание, т.е. срезание части эвольвенты вблизи основной окружности, что снижает несущую способность передачи (рис.5).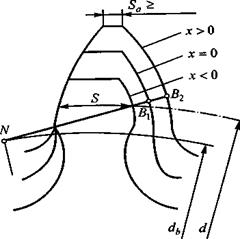
 ) (рис.6).
) (рис.6).
 - угол между линией К2К2 и осью основного цилиндра. Делительный угол
- угол между линией К2К2 и осью основного цилиндра. Делительный угол 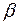 определяется на делительном цилиндре и берется в пределах 8 … 200 (для шевронных 25 …450). Он является исходным при проектировании передачи, а основной угол наклона определяется в зависимости от
определяется на делительном цилиндре и берется в пределах 8 … 200 (для шевронных 25 …450). Он является исходным при проектировании передачи, а основной угол наклона определяется в зависимости от 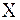 геометрические па-раметры зубчатых колес могут быть определены по следующим формулам:
геометрические па-раметры зубчатых колес могут быть определены по следующим формулам: =0)
=0)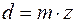 ; (2)
; (2) ; (3)
; (3)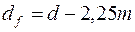 ; (4)
; (4)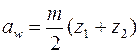 ; (5)
; (5)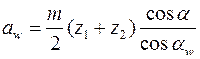 , (6) где угол
, (6) где угол  находится из соотношения
находится из соотношения ; (7)
; (7) стандартный угол зацепления (
стандартный угол зацепления ( 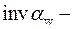 эвольвентная функция (
эвольвентная функция (  (табл.П1.1); суммарный коэффициент смещения
(табл.П1.1); суммарный коэффициент смещения  определяется по формуле
определяется по формуле . (8)
. (8) ; (основное отклонение
; (основное отклонение 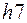 ); (9)
); (9) ; (10)
; (10)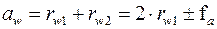 , (11) где
, (11) где  допуск на межосевое расстояние;
допуск на межосевое расстояние; . (12)
. (12) . (13)
. (13) , где
, где  - коэфициент (14) уравнительного смещения.
- коэфициент (14) уравнительного смещения.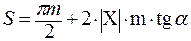 ; (15) на окружности вершин
; (15) на окружности вершин . (16)
. (16)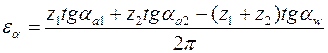 , (17) где
, (17) где  ;
;  .
.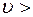 10 м/с) 5, 6, 7, тихоходных – 8, 9. Для степеней точности 1 и 2 допуски не установлены.
10 м/с) 5, 6, 7, тихоходных – 8, 9. Для степеней точности 1 и 2 допуски не установлены. 1 мм) и ГОСТ 9178-81 (для колес с
1 мм) и ГОСТ 9178-81 (для колес с  мм) устанавливаются нормы: кинематической точности, плавности работы и контакта зубьев.
мм) устанавливаются нормы: кинематической точности, плавности работы и контакта зубьев. .Допуск на кинематическую погрешность передачи обозначается
.Допуск на кинематическую погрешность передачи обозначается  .
.
 (рис.9).
(рис.9). .Установлены также кинематическая погрешность зубчатого колеса на
.Установлены также кинематическая погрешность зубчатого колеса на  ша-гах
ша-гах 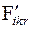 , накопленная погрешность
, накопленная погрешность  и допуск на накопленную погрешность
и допуск на накопленную погрешность  (рис.10).
(рис.10).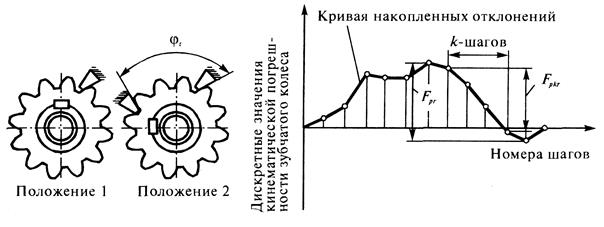
 . При этом под действительной длиной общей нормали понимается расстояние между двумя параллельными плоскостями, касательны-ми к двум разноименным активным боковым поверхностям зубьев зубчатого колеса. Допуск на колебание длины общей нормали -
. При этом под действительной длиной общей нормали понимается расстояние между двумя параллельными плоскостями, касательны-ми к двум разноименным активным боковым поверхностям зубьев зубчатого колеса. Допуск на колебание длины общей нормали -  .
.
 )/
)/  ]×100%, так и по его высоте (
]×100%, так и по его высоте ( 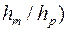 ×100%=(
×100%=( 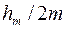 )×100% (рис.13).
)×100% (рис.13).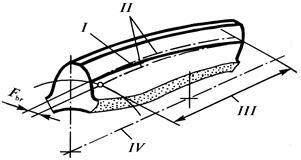


 …).
…). , т.е. наименьший возможный боковой зазор. Вид допуска характеризует возможный наибольший боковой зазор. Допуск на боковой зазор обозначается
, т.е. наименьший возможный боковой зазор. Вид допуска характеризует возможный наибольший боковой зазор. Допуск на боковой зазор обозначается  .
. 1 мм установлено шесть видов сопряжений колес в передаче (A, B, C, D, E, H) и восемь видов допуска
1 мм установлено шесть видов сопряжений колес в передаче (A, B, C, D, E, H) и восемь видов допуска 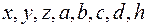 ).
).
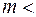 1 мм передач с нерегулируемым и регулируемым расположением осей устанавливается пять видов сопряжений (D, E, F, G, H) и четыре вида допуска на боковой зазор (
1 мм передач с нерегулируемым и регулируемым расположением осей устанавливается пять видов сопряжений (D, E, F, G, H) и четыре вида допуска на боковой зазор (  ), при этом видам сопряжений D и E соответствует вид допуска на боковой зазор
), при этом видам сопряжений D и E соответствует вид допуска на боковой зазор  , а видам сопряжений F, G, H - виды допусков
, а видам сопряжений F, G, H - виды допусков 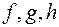 соответственно.
соответственно.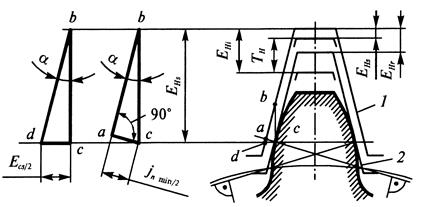
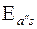 ; нижнее -
; нижнее -  ;
; . Средней длиной общей нормали
. Средней длиной общей нормали  называют среднее арифметическое из всех действительных длин общей нормали по зубчатому колесу (рис.19)
называют среднее арифметическое из всех действительных длин общей нормали по зубчатому колесу (рис.19) . (18)
. (18) . Допуск на среднюю длину общей нормали обозначается
. Допуск на среднюю длину общей нормали обозначается  .
. . Отклонение длины общей нормали (разность значений действительной и номинальной длины общей нормали) -
. Отклонение длины общей нормали (разность значений действительной и номинальной длины общей нормали) - 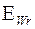 . Наименьшее отклонение длины общей нормали (наи-меньшее предписанное отклонение длины общей нормали, осуществляемое с целью обеспечения в передаче гарантированного бокового зазора) для зубча-того колеса с внешними зубьями обозначается -
. Наименьшее отклонение длины общей нормали (наи-меньшее предписанное отклонение длины общей нормали, осуществляемое с целью обеспечения в передаче гарантированного бокового зазора) для зубча-того колеса с внешними зубьями обозначается -  , с внутренними зубьями - +
, с внутренними зубьями - +  . Допуск на длину общей нормали -
. Допуск на длину общей нормали -  .
.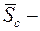 толщина зуба по постоянной хорде, отнесенная к нормальному сечению, соответствующая номи-нальному положению исходного контура. Отклонение толщины зуба (разность между действительной и номинальной толщинами зуба по постоянной хорде) обозначают
толщина зуба по постоянной хорде, отнесенная к нормальному сечению, соответствующая номи-нальному положению исходного контура. Отклонение толщины зуба (разность между действительной и номинальной толщинами зуба по постоянной хорде) обозначают  . Наименьшее предписанное уменьшение постоянной хорды, осуществляемое с целью обеспечения в передаче гарантированного бокового зазора, называется наименьшим отклонением толщины зуба
. Наименьшее предписанное уменьшение постоянной хорды, осуществляемое с целью обеспечения в передаче гарантированного бокового зазора, называется наименьшим отклонением толщины зуба  . Допуск на толщину зуба обозначается
. Допуск на толщину зуба обозначается  .
. под которым понимается расчетный размер по верху роликов (или между роли-ками при контроле зубчатых колес с внутренними зубьями), соответствующий номинальному положению исходного контура (рис.20).
под которым понимается расчетный размер по верху роликов (или между роли-ками при контроле зубчатых колес с внутренними зубьями), соответствующий номинальному положению исходного контура (рис.20). , (19)
, (19) диаметр окружности, на которой лежит центр ролика; определяет-ся по формуле
диаметр окружности, на которой лежит центр ролика; определяет-ся по формуле ; (20)
; (20) эвольвентный угол, соответствующий указанной окружности.
эвольвентный угол, соответствующий указанной окружности.  может быть определен из соотношения
может быть определен из соотношения ; (21)
; (21) диаметр ролика (шарика) (рекомендуется
диаметр ролика (шарика) (рекомендуется  (1,7…1,9)
(1,7…1,9)  .
. . Наименьшее отклонение размера по роликам для зубчатого колеса с внешними зубьями обозначают
. Наименьшее отклонение размера по роликам для зубчатого колеса с внешними зубьями обозначают 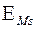 , для зубчатого колеса с внутренними зубьями - +
, для зубчатого колеса с внутренними зубьями - +  . Допуск на размер по роликам -
. Допуск на размер по роликам -  . При контроле размера по роликам величины
. При контроле размера по роликам величины  ;
;  , (22)
, (22) угол профиля в точке на концентрической окружности зубчатого колеса, проходящей через центр ролика (определяется при геометрическом расчете размера по роликам);
угол профиля в точке на концентрической окружности зубчатого колеса, проходящей через центр ролика (определяется при геометрическом расчете размера по роликам); угол наклона зуба на основном цилиндре.
угол наклона зуба на основном цилиндре. рассчитывается по формуле
рассчитывается по формуле (23)
(23) определяются по табл.П.2.8,9 и П.3.8,9.
определяются по табл.П.2.8,9 и П.3.8,9. - часть коэффициента осевого перекрытия передачи, определяемая с учетом действительного суммарного пятна контакта в передаче.
- часть коэффициента осевого перекрытия передачи, определяемая с учетом действительного суммарного пятна контакта в передаче. с допуском на боковой зазор -
с допуском на боковой зазор -