
|
|
Сравнить теоретическое и экспериментальное значение логарифмического декремента из пп.7,8 с учетом ошибок измерений и сделать вывод.Лабораторная работа №3
ИЗУЧЕНИЕ ТЕОРИИ ЗАТУХАЮЩИХ КОЛЕБАНИЙ ПРУЖИННОГО МАЯТНИКА
Цель работы
Задачей данной работы является ознакомление с простей-шим случаем затухающих колебаний пружинного маятника
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ - набор пружин и грузов - измерительная установка для отсчета отклонений грузов - секундомер
МЕТОДИКА ПРОВЕДЕНИЯ ЭКСПЕРИМЕНТА
Пружинный маятник – это грузик, подвешенный на пру-жине (рис. 3.1). После отклонения от положения равновесия он будет совершать вертикальные гармонические колеба-ния, если упругая пружина такова, что сила деформации пропорциональна величине удлинения пружины ( 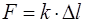 , где , где  – коэффициент упругости). – коэффициент упругости).
Колебания грузика описываются уравнением:
Это – дифференциальное уравнение собственных незату-хающих колебаний с частотой:
Если в колеблющейся системе действуют диссипативные силы типа сил трения, пропорциональные скорости, то ко-лебания системы будут затухающими (рис. 3.2).
Уравнение колебаний будет иметь вид:
где Решение дифференциального уравнения (3.2) имеет вид:
Из выражения (3.3) видно, что амплитуда колебаний уменьшается со временем по закону:
Период затухающих колебаний больше периода собст-венных незатухающих колебаний:
Затухание колебаний принято характеризовать логариф-мическим декрементом затухания:
Учитывая, что
Пусть
откуда
Для пружинного маятника, колеблющегося в воздухе, ве-личина логарифмического декремента лежит в пределах от 0,01 до 0,1. Из теории затухающих колебаний следует, что вид Энергия колебательного движения изменяется по закону
где Из (3.10) видно, что энергия осциллятора расходуется на работу против диссипативных сил и превращается во внут-реннюю энергию. Мощность потерь, т.е. скорость рассеяния энергии, с од-ной стороны,
а с другой, с учетом (3.10),
Качество колебательной системы, ее способность сохра-нять запасенную энергию характеризуется добротностью Q, которая определяется отношением запасенной энергии к потерям за время
C учетом (3.11) выражение для добротности принимает вид:
Из (3.13) следует, что добротность колебательной сис-темы равна числу колебаний за время
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.
Упражнение 1
1.Эксперимент проводят по схеме рис. 3.1. 2. Несколько раз (4-5) измерить время
Вычислить среднее значение периода
Таблица 1 Определение среднего значения периода
Упражнение 2
3. Установить первоначальное значение амплитуды (наибольшее отклонение от положения равновесия)
Таблица 2
4. Вычислить значение коэффициента затухания:
и его абсолютную ошибку
где 5. Вычислить коэффициент сопротивления:
и его абсолютную ошибку
6. Рассчитать время релаксации:
и его абсолютную ошибку
7. Рассчитать значение логарифмического декремента затухания:
и его абсолютную ошибку
где 8. Вычислить теоретическое значение логарифмического декремента затухания
взяв значение Найти относительную ошибку
где Рассчитать абсолютную ошибку
Сравнить теоретическое и экспериментальное значение логарифмического декремента из пп.7,8 с учетом ошибок измерений и сделать вывод. 9. Вычислить значение добротности:
используя значение Рассчитать относительную ошибку добротности, исполь-зуя относительные ошибки
и абсолютную ошибку
Упражнение 3
10. Одеть на грузик пластину для увеличения сопротив-ления воздуха. Схема эксперимента представлена на рис. 3.3. Повторить пп. 3-9. Результаты занести в таблицу 3, анало-гичную таблице 2. Сравнить полученные значения коэффи-циента затухания
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Оцените относительную ошибку в определении 2. Сформулируйте основное предположение метода наи-меньших квадратов (МНК), используйте МНК при постро-ении графиков. 3. Начертите график Т2=f(m) по МНК. 4. Оцените абсолютную и относительную ошибку при из-мерении массы. 5. Оцените абсолютную и относительную ошибку в опре-делении 6. Начертите график Т2=f(m) по МНК. 7. Найдите по графику среднее значение К. 8. Оцените, совпадают ли и с какой точностью значения Кi, полученные по графику и рассчитанные в упражнении 1. 9. Объясните, почему не рекомендуется брать большие зна-чения начальной амплитуды А0? 10. Оцените относительную погрешность измерения А0 и А(t), 11. Оцените относительную погрешность определения ло-гарифмического декремента затухания 12. Оцените относительную погрешность определения ко-эффициента сопротивления b. 13. Оцените абсолютную и относительную погрешность определения периода (в упражнении 1) . 14. Выведите уравнение для энергии затухающих колеба-ний в зависимости от времени, нарисуйте график. 15. Объясните, что характеризует время релаксации (пос-тоянная времени затухания). 16. Оцените мощность потерь энергии. 17. Укажите, как связаны добротность и время релакса-ции. 18. Выведите уравнение затухающих колебаний? 19. Чем определяется период затухающих колебаний? 20. Как зависит от времени амплитуда затухающих ко-лебаний? 21. Как связан логарифмический декремент затухания и амплитуда колебаний? 22. Как связан логарифмический декремент затухания с коэффициентом сопротивления и периодом? 23. Выведите выражение для энергии затухающих коле-баний. 24. Как связаны потери энергии и добротность? 25. Определите выражение для добротности контура. 26. Как связаны добротность и логарифмический декре-мент затухания? 27. Определите время релаксации. Свяжите его с коэф-фициентом сопротивления и логарифмическим декремен-том. 28. Какими являются колебания в данной работе – зату-хающими или незатухающими? 29. При каком значении коэффициента сопротивления ко-лебания прекращаются? 30. Чем отличаются колебания пружинного маятника в го-ризонтальной и вертикальной плоскости?

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


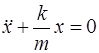 . (3.1)
. (3.1) .
.
 , (3.2)
, (3.2) – коэффициент затухания колебаний.
– коэффициент затухания колебаний. . (3.3)
. (3.3)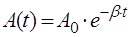 . (3.4)
. (3.4) , (3.5)
, (3.5) . (3.6)
. (3.6) . (3.7)
. (3.7) ,
, . (3.8)
. (3.8) будет отклонение, которое имеет место через время
будет отклонение, которое имеет место через время  , т.е. через
, т.е. через  колебаний после отклонения
колебаний после отклонения  . Тогда можно записать:
. Тогда можно записать: ,
, ,
, (3.9)
(3.9) имеет вид прямой. Здесь
имеет вид прямой. Здесь  – амплитуда колебания.
– амплитуда колебания. , (3.10)
, (3.10) – постоянная времени затухания (время релаксации), показывающая, что амплитуда колебания уменьшается за время
– постоянная времени затухания (время релаксации), показывающая, что амплитуда колебания уменьшается за время  раз.
раз.  .
. ,
, . (3.11)
. (3.11)
 . (3.12)
. (3.12) . (3.13)
. (3.13) ; причем за это время амплитуда уменьшается в
; причем за это время амплитуда уменьшается в  раза, а энергия в
раза, а энергия в  раз.
раз. , за которое гру-зик совершит
, за которое гру-зик совершит  колебаний. Полученные значения занести в таблицу 1. Вычислить средний период затухаю-щих колебания по формуле:
колебаний. Полученные значения занести в таблицу 1. Вычислить средний период затухаю-щих колебания по формуле: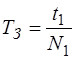 .
. , абсолютную
, абсолютную  и относительную ошибку измерений. Результат занести в таблицу 1.
и относительную ошибку измерений. Результат занести в таблицу 1.



 око-ло 5 см. Отпустив грузик, одновременно измерить время
око-ло 5 см. Отпустив грузик, одновременно измерить время  и число полных колебаний
и число полных колебаний  , за которое амплитуда умень-шится на 50% от первоначальной величины:
, за которое амплитуда умень-шится на 50% от первоначальной величины: 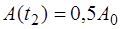 . Провести данный опыт не менее 5 раз при одном и том же значении
. Провести данный опыт не менее 5 раз при одном и том же значении  и
и  , Результат занести в таблицу 2.
, Результат занести в таблицу 2.
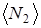




 ,
, – относительная ошибка
– относительная ошибка  .
.


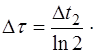


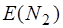 – относительная ошибка
– относительная ошибка  .
. ,
,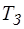 из п.2, а значение
из п.2, а значение  – из п.4.
– из п.4.
 и
и 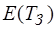 – относительные ошибки
– относительные ошибки 

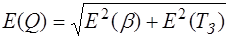
 .
. , сделать выводы.
, сделать выводы.
 (наклона прямой).
(наклона прямой).