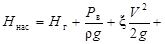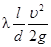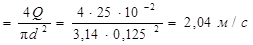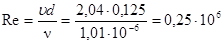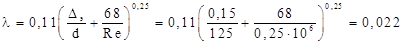|
|
Средние значения плотности r и кинематическойЗадания по Гидрогазодинамике на 2015 год (Определяются последней цифрой зачетной книжки (шифр)
Задания по теории предмета Т1. Пьезометрическая и вакуумметрическая высоты. Пьезометрические плоскости. Уравнение Бернулли для струйки реального газа. Т2. Скорость и расход истечения жидкости через отверстие в тонкой стенке. Уравнение Бернулли для газа при установившемся движении. Т3. Сила гидростатического давления на криволинейную поверхность (как векторная сумма проекций на координатные оси). Уравнение неразрывности в газе. Т4. Относительный покой жидкости в цилиндрическом сосуде, вращающемся относительно вертикальной оси. Расчет газопроводов. Т5. Уравнение Бернулли для потока вязкой несжимаемой жидкости. Уравнение равновесия газов. Т6. Формулы для расчета потери напора в трубах. Зависимость коэффициента гидравлического трения от числа Рейнольдса и относительные шероховатости. Расчет газопроводов при малых перепадах давления. Т7. Основное уравнение гидростатики и закон Паскаля. Уравнение состояние газов. Т8. Особенности гидравлического расчета газопроводов. Уравнение газопроводов при больших перепадах давления. Т9. Действительные рабочие характеристики центробежногонасоса.Истечение газа через насадок. Т10. Определение пропускной способности трубопровода. Особенности расчета трубопроводов пневмотранспорта. РАСЧЕТНЫЕ ЗАДАЧИ Тема: Физические свойства жидкостей Задача 1. Автоклав объемом 25л наполнен жидкостью и закрыт герметически, коэффициент температурного расширения жидкости a, ее модуль упругости Е. Определить повышение давления в автоклаве при увеличении температуры жидкости на величину Т, объемной деформацией автоклава пренебречь.
Указания: При решении задачи используют известные формулы для определения коэффициентов объемного сжатия и температурного расширения жидкости. Интересно, что повышение давления в герметичном заполненном жидкостью сосуде не зависит от его объема. Задача 2. Определить скорость υ равномерного скольжения прямоугольной пластины (aхbхс) по наклонной плоскости под углом a= 12о, если между пластиной и плоскостью находится слой масла толщиной d(рис.7). Температура масла 30°С, плотность материала пластины r=7850 кг/м3.
Рис.1
Задача 3. Зазор между валом и втулкой заполнен маслом, толщина слоя которого равна d. Диаметр вала D, длина втулки L. Вал вращается равномерно под воздействием вращающего момента М. Определить частоту вращения вала, если температура масла равна 40 °С.
рис.2
Указание: При решении задач 2,3 применяется формула И. Ньютона.
Поскольку толщина слоя масла мала, можно считать, что скорости в нем изменяются по прямолинейному закону. Эпюра касательных напряжений в слое масла принимается прямоугольной; сила трения проходит через центр тяжести этой эпюры. В задачах 2,3 важно увидеть параллель хода решения этих задач, и перед решением задачи 3 следует рассмотреть задачу 2. Задачи решаются с помощью формулы Ньютона: T=hA(dυ/dn), где T- сила трения; h - динамическая вязкость жидкости; А - площадь соприкосновения твердой поверхности с жидкостью; (dυ/dn) - градиент скорости. Задачу 3 решают по той же методике, с учетом законов вращательного движения. Силу трения в этом случае определяют из формулы момента: М=Т( D/2 + d/2) Из-за малости зазора вторым членом в скобках можно пренебречь. Рассматривая движение в зазоре как плоскопараллельное, т.е. считая, что скорости в слое масла изменяются по прямолинейному закону, то угловую скорость w и частоту вращения вала n определяют по известным формулам механики: υ=w D/2, w=2pn Тема: Гидростатика Задача 4. Круглое отверстие радиуса R в дне резервуара с жидкостью плотностью r перекрывается клапаном-полусферой такого же радиуса, вес которой G. Вычислить силу Т необходимую для поднятия клапана при напоре Н если давлениена свободной поверхности ро.
Рис.3
Задача 5. Найти силу давления масла на круглую крышку люка диаметром d, которая закрывает отверстие в стенке имеющей угол уклона a. Расстояние от уровня масла до верха люка h. Найти точку приложения равнодействующей силы.
Рис.4
Задача 6. Паровой прямодействующий насос, подает жидкость Ж, на высоту Н (рис.11). Каково абсолютное давление пара, если диаметр парового цилиндра D, а насосного цилиндра d. Потерями на трение пренебречь.
Рис.5
Тема: Гидродинамика Задача 7. С помощью водомера Вентури определить расход воды Q, протекающей по трубе диаметром D, если диаметр вставки d, а разность пьезометрических высот Н.
.
Задача 8. Из одного водоема в другой вода переливается с помощью сифонного трубопровода, на котором имеется колено и решетка. Определить диаметр сифона, построить пьезометрическую линию.
Рис.7
Задача 10.Центробежный насос, характеристика которого задана, подает воду на геометрическую высоту НГ (рис. 15). Трубы всасывания и нагнетания, изготовленные из материала М, соответственно имеют диаметр dВ и dН, а длину lВ и lН. Температура подаваемой воды Т˚С. Найти рабочую точку при работе насоса на сеть. Определить, как изменяется напор и мощность насоса при уменьшении задвижкой подачи воды на 25%. Построить график характеристик насоса по данным таблицы.
Указание: на входе установлен шаровой клапан, вентиль и фильтр (см. также рис. 6). Для фильтра условно принять ζ=20.
Рис.8
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ Пример: определить величину и точку приложения силы гидростатического давления воды на щит шириной b=2м, если глубина воды перед щитом H=2,7м.
Сила давления воды на щит: рис.9
Расстояние точки приложения этой силы от свободной поверхности воды:
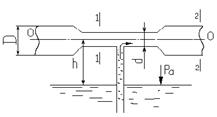
Пример: определить диаметр d суженной части трубы, при котором вода поднимается на высоту h=3,5м (рис. 17). Расход воды Q=6л/с, диаметр D=10см.
Рис.10 Решение: Сечение1-1 принимаем в суженной части трубы, где нужно определить d, сечение 2-2 – на выходе из расширенной части трубы, где давление равно атмосферному (р2=ра). Плоскость сравнения совместим с осью трубы, тогда z1=z2=0. С учетом этого уравнение Бернулли получим в виде: Для того чтобы вода поднялась из резервуара на высоту h, удельная энергия давления на поверхности воды в резервуаре ратм/ρg должна быть на величину h выше, чем удельная энергия давления в сечении 1-1, т.е.:
Решая совместно эти уравнения, получим:
Скорости воды в сечении 1-1 и 2-2:
Подставляя эти величины в последнее уравнение, и решая его относительно диаметра суженной части, получим:
Пример:найти потерю давления на трение при движении воды с температурой Т=50˚С в цельносварной стальной трубе, бывшей в эксплуатации, с внутренним диаметром d=0,5м. Расход воды Q=0,6 м3/с. Длина трубы l=500 м. Решение: Находим по таблице значение абсолютной эквивалентной шероховатости трубы ∆экв=0,15 мм = 0,15∙10-3м, ∆экв /d=0,0003. Кинематический коэффициент вязкости для воды заданной температуры ν=0,55∙10-6 м2/с. Средняя скорость течения воды в трубе и число Рейнольдса:
Значение коэффициента гидравлического трения:
Потери напора на трение:
Плотность воды находим из таблицы приложения по температуре – ρ=988 кг/м3. Потери давления на трение:
Пример:вода при температуре Т=20˚С перекачивается насосом из открытого бака А в резервуар В (рис.15), где поддерживается постоянное давление РВ=0,075 МПа (избыточное) по трубопроводу общей длиной l=112м и диаметром d=125мм. Разность уровней воды в баках НГ=25м. Определить напор, создаваемый насосом для подачи в бак В расхода воды Q=25 л/с. Принять суммарный коэффициент местных сопротивлений ξ=6,5. Эквивалентная шероховатость стенок трубопровода ∆Э=0,15мм. Решение: Напор, создаваемый насосом:
Средняя скорость течения воды в трубе:
Число Рейнольдса для потока воды в трубе:
Значение коэффициента гидравлического трения
Величина напора:
ПРИЛОЖЕНИЯ Средние значения плотности r и кинематической 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

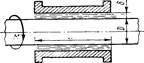
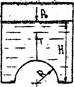

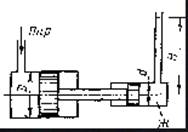
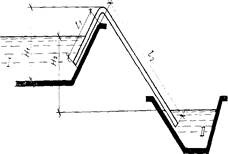 Рис.6
Рис.6 Задача 9. Определить скорость и напор воды через отверстие диаметром d, в тонкой стенке резервуара при постоянном напоре Н.
Задача 9. Определить скорость и напор воды через отверстие диаметром d, в тонкой стенке резервуара при постоянном напоре Н.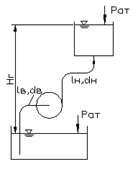
 Решение:
Решение: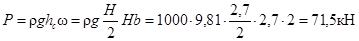

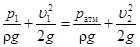
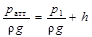
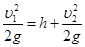

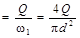 ;
; 
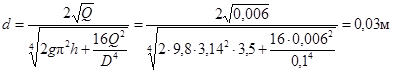


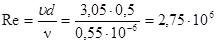
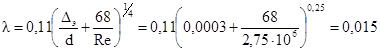
 м.вод.ст.
м.вод.ст.