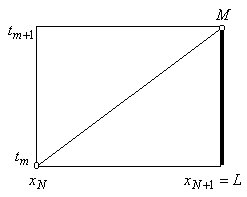|
|
Лабораторная работа №4. «Расчет гидравлического удара на участке трубопровода»Теоретическое введение
Неустановившимися (или нестационарными) процессами в нефте- и нефтепродуктопроводах называются такие процессы, в которых характеристики потока жидкости изменяются не только от сечения к сечению, но и в каждом сечении в зависимости от времени. Изменяются давление, скорость и расход жидкости, температура потока и др. Иными словами, в неустановившемся течении все эти параметры являются функциями не только от координаты сечения, но и от времени, то есть Неустановившиеся режимы течения жидкости связаны с различными технологическими операциями, осуществляемыми при перекачке. Пуск и остановка трубопровода, включение или отключение дополнительного агрегата на головной или промежуточной нефтеперекачивающей станции, полное или частичное открытие задвижки, переключение резервуаров, начало или прекращение сброса или подкачки жидкости, разрыв трубопровода и т. д. – все это приводит к тому, что в трубопроводе начинаются изменения. Такие изменения в виде волн давления и расхода жидкости распространяются вверх и вниз по потоку от места, где они генерированы. Возникшие изменения продолжаются в трубопроводе, как правило, до установления нового режима транспортирования, поэтому неустановившиеся процессы называют еще переходными режимами. Плотности транспортируемых жидкостей достаточно высоки, их скорости движения также не малы, поэтому поток жидкости в трубопроводе имеет вполне ощутимую инерцию, учетом которой нельзя пренебрегать при совершении той или иной технологической операции. Так, например, резкая остановка потока нефти или нефтепродукта в трубопроводе при быстром закрытии задвижки приводит к скачкообразному росту давления, измеряемому несколькими атмосферами. Возникшее повышение с большой скоростью распространяется от места остановки потока в виде волны давления, способной разорвать трубу и привести к аварии. Подобное явление называется гидравлическим ударом. Включение нефтеперекачивающей станции на закрытую задвижку также может вызвать скачкообразное повышение давления, чреватое опасностью для целостности трубопровода. Отключение нефтеперекачивающей станции приводит к повышению давления в линии всасывания и к падению давления в линии нагнетания. И то, и другое представляет скрытую угрозу для трубопровода. Повышение давления перед станцией вызывает дополнительную нагрузку на трубопровод, способную вызвать его разрыв. Можно утверждать, что вообще, всякое замедление или ускорение потока тяжелой жидкости в трубопроводе вызывает колебания давления в трубе и должно осуществляться с чрезвычайной осторожностью. Рассмотрим течение жидкости плотностью
Рис. 17. Схема возникновения волны давления
Рассмотрим уравнения баланса массы и количествадвижения для возмущенного участка трубопровода. Баланс массы. Изменение
или
Найдем относительные изменения Относительное изменение
где Относительное изменение
Рис.18. К выводу формулы изменения площади поперечного сечения трубопровода при изменении давления
Согласно этому методу, рассматривается равновесие верхней половины трубы (выделенной на рис.18 утолщенной линией) под действием разности давлений
где d0=0,5(D+d) – диаметр срединного волокна
Здесь Подставив
Здесь
Подставив результаты (4.2) и (4.4) в формулу (4.1), получим равенство:
позволяющее установить связь изменения Баланс количества движения (импульса). При изменении скорости течения происходит изменение количества движения возмущенного объема жидкости. Это изменение равно: Согласно известной теореме механики, изменение количества движения системы материальных точек равно импульсу всех внешних сил, действующих на эту систему, т.е.
связывающую изменение давления Если принять, что скорость
Формула (4.6)представляет собой знаменитую формулу выдающегося русского ученого-механика, “отца русской авиации”, Н.Е.Жуковского. Формула Жуковского гласит, что всякое изменение скорости течения жидкости в трубопроводе вызывает пропорциональное ему изменение давления и наоборот, изменение давления в потоке жидкости, текущей в трубопроводе, приводит к пропорциональному изменению скорости течения. Подставляя (4.6) в (4.5), получаем вторую формулу Н.Е.Жуковского:
или
устанавливающую связь скорости распространения волн возмущения в трубопроводе с параметрами жидкости и самого трубопровода. Пример 1. Рассчитать скорость Решение. По формуле (4.7) находим:
Пример 2. Рассчитать изменение Решение. По формуле (4.7) находим:
По формуле (4.6) рассчитываем
Гидравлический удар в трубопроводах. Суть гидравлического удара состоит в том, что стационарное течение жидкости в трубопроводе нарушается путем резкого закрытия (или открытия) задвижки, включения (или отключения) насоса и т.д., в результате чего происходит резкое торможение (или ускорение) потока и ударное сжатие ее частиц. Фронт, на котором происходит изменение гидродинамических параметров жидкости, имеет относительно малую протяженность и в виде волны давления распространяется по потоку. Аналогичное явление возникает в трубопроводе и в других случаях, когда происходит скачкообразное изменение скорости (расхода) жидкости. Возможность гидравлического удара следует учитывать при проектировании и эксплуатации нефте- и нефтепродуктопроводов, поскольку ударное давление может намного превысить допустимые нормы, привести к разрыву трубы и возникновению аварийной ситуации. Скорость распространения волн гидравлического удара в стальных трубопроводах близка к значению 1000 м/с, а изменение скорости течения на 1 м/с вызывает изменение давления примерно на 9,0 атм. Необходимость считаться с разрушительной силой гидравлического удара в трубопроводах, транспортирующих капельные жидкости (нефть, нефтепродукты, воду и т.п.), выражается в том, что на подобных трубопроводах (в отличие от газопроводов) никогда не устанавливают краны, быстро перекрывающие сечение трубопровода. На них применяют вентильные задвижки, дающие медленное перекрытие сечения и обеспечивающие безопасную остановку потока жидкости. Более того, в ряде случаев на нефтеперекачивающих станциях применяют специальные устройства, призванные защитить трубопровод от последствий гидравлического удара. Например, на линиях всасывания нефтеперекачивающих станций устанавливают гасители гидравлического удара на случай, если станция внезапно отключится, и давление перед ней начнет повышаться. Принцип действия гасителей гидравлического удара состоит в отводе части жидкости из трубопровода в специальный резервуар для снижения темпа нарастания давления. На линиях нагнетания нефтеперекачивающих станций устанавливают системы автоматического регулирования, одна из задач которых состоит в защите станций от ударных волн давления, распространяющихся вверх по потоку и приходящих с предыдущего участка. Впервые правильное объяснение гидравлического удара дал Н.Е.Жуковский в конце прошлого века. Его исследования были выполнены на Московской водопроводной станции, а сама работа “О гидравлическом ударе в водопроводных трубах” (1899) стала классической работой известной во всем мире. Н.Е.Жуковский впервые связал величину ударного давления Волны гидравлического удара, генерируемые в нефте- и нефтепродуктопроводах резкими изменениями скорости потока, могут распространяться на значительные расстояния, постепенно затухая вследствие диссипации механической энергии за счет сил вязкого трения. Наибольшую опасность волны повышенного давления представляют для тех участков трубопровода, где и без того существовало достаточно высокое статическое давление. Такие участки находятся вблизи нефтеперекачивающих станций, а также в наиболее низких сечениях трубопровода. В последних может быть высоким пьезометрический напор Но и волны снижения давления могут вызывать опасные явления. В наиболее высоких сечениях трубопровода могут возникать парогазовые скопления, которые при возврате к стационарному режиму исчезают далеко не сразу. При этом они значительно уменьшают расход перекачки и вызывают повышенную вибрацию трубопровода. Пример 1. Рассчитать ударное изменение Решение. Сначала находим скорость
Затем по формуле (4.7) находим скорость волн давления:
Наконец, по формуле (4.6) рассчитываем Пример 2. Оператор нефтеперекачивающей станции совершил ошибку, включив станцию на закрытую задвижку. В результате нефть Решение. Сначала находим скорость
По формуле (4.7) находим скорость волн давления:
По формуле (4.6) рассчитываем Пример 3. На сколько атмосфер понизится давление за мгновенно закрывшейся задвижкой, перекрывшей поток нефти Решение. Находим скорость
По формуле (4.7) находим скорость волн давления:
По формуле (4.6) рассчитываем Если давление в месте установки задвижки было ниже
Дифференциальные уравнения нестационарного движения жидкости в трубопроводе. Система таких уравнений имеет вид [5]:
где
Метод характеристик.Расчет нестационарных режимов работы нефте- или нефтепродуктопровода более сложен, чем расчет стационарных режимов. Не существует простых алгебраических формул для вычисления параметров потока в нестационарных режимах хотя бы потому, что таких режимов существует бесчисленное множество. Поэтому расчеты нестационарных режимов работы нефтепровода, например, поименованных в начале этого параграфа, осуществляют численно с использованием компьютеров. Приведем один из эффективных алгоритмов расчета, называемый методом характеристик, послуживший основой для той компьютерной программы, которая представлена в настоящем Практикуме. Умножим второе уравнение системы уравнений (4.8) на
Аналогичным образом после вычитания второго уравнения системы (4.8), умноженного на
Если на плоскости переменных
и которые называются характеристиками системы дифференциальных уравнений (4.8), можно заметить, что для любого параметра
Это означает, что выражение, стоящее слева, есть производная от функции
то есть выражение, стоящее слева, является производной от функции Используя понятие производной по направлению, полученные уравнения можно записать в следующем виде:
или
Система (4.9) называется характеристической формой системы (4.8). Если При Пусть, например, в какой-либо момент времени
Рис.19. Расчетная схема метода характеристик
Через узлы получившейся сетки проведем характеристики Заменим производные по направлению в уравнениях (4.9) конечными разностями вдоль характеристик
где
Отсюда получаем систему уравнений для определения давления
или
где
Таким образом, рекуррентные формулы (4.10) в принципе решают поставленную задачу о расчете нестационарных процессов в трубопроводе, поскольку позволяют рассчитать значения давлений и скоростей течения в последующий момент времени по известным значениям этих параметров в предыдущий момент времени. За первый «предыдущий» момент времени можно взять начальное состояние потока (т.е. значения давлений и скоростей течения в момент времени, принимаемый за начальный
Начальные и краевые условия. Пусть исследуется нестационарный режим работы участка трубопровода с протяженностью * каким было исходное состояние участка трубопровода, * что происходит на краях участка (т.е. в сечениях Первая информация определяется так называемым начальным условием, а вторая – краевыми. Заметим, что формулы (4.10) позволяют определить значения Состояние участка трубопровода в начальный момент времени может быть произвольным, но очень часто в качестве начального состояния берется стационарный режим перекачки, в котором известны распределения напора и расхода. Пусть, например, в стационарном режиме перекачки известен расход нефти
или
где Для нахождения значений
Рис.20. Краевое условие в начале участка трубопровода
Система уравнений (4.12) служит для расчета значений В правое сечение (
Рис.21. Краевое условие в конце участка трубопровода
Задания лабораторной работы
Основное задание. Перекачка продукта (плотность – ρ, кинематическая вязкость – ν, давление упругости насыщенных паров – pу, модуль упругости – K=1250 МПа) ведется в стальном трубопроводе (модуль Юнга стали E=2·105 МПа). Трубопровод имеет длину L=50 км, внешний диаметр D=530 мм, толщину стенки δ=8 мм и абсолютную шероховатость внутренней поверхности труб Δ=0,2 мм. Перекачка ведется двумя центробежным насосами НМ 1250-260. Подпор перед нефтеперекачивающей станцией составляет hп = 40 м, давление в конце участка трубопровода равно pк = 0,30 МПа. Определить минимальное время τmin закрытия задвижки в конце трубопровода, необходимое для того, чтобы темп роста давления в волне гидравлического удара, приходящей на нефтеперекачивающую станцию не превышал 0,1 МПа/с. Исходные данные к расчету по вариантам представлены в таблицах 7, 8.
Таблица 7 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
,  ,
,  ,
,  .
. со скоростью
со скоростью  в трубопроводе с площадью поперечного сечения
в трубопроводе с площадью поперечного сечения  , рис.17. Пусть в сечении
, рис.17. Пусть в сечении  возникает некоторое изменение
возникает некоторое изменение  скорости этого течения, например, замедление потока, т.е. новая скорость течения
скорости этого течения, например, замедление потока, т.е. новая скорость течения  . Что происходит при этом? Слои жидкости, идущей сзади, тормозятся и сдавливают слои жидкости, идущей впереди. При этом давление в жидкости возрастает от значения
. Что происходит при этом? Слои жидкости, идущей сзади, тормозятся и сдавливают слои жидкости, идущей впереди. При этом давление в жидкости возрастает от значения  до
до  , плотность жидкости увеличивается от
, плотность жидкости увеличивается от  , площадь сечения трубопровода также возрастает от
, площадь сечения трубопровода также возрастает от  до
до  , а сама область возмущения расширяется с некоторой скоростью
, а сама область возмущения расширяется с некоторой скоростью  (на рис. 17 эта область имеет протяженность
(на рис. 17 эта область имеет протяженность  ). Конечно, изменения
). Конечно, изменения  плотности жидкости
плотности жидкости  площади сечения трубопровода невелики и на глаз незаметны, однако оказывается, что те и другие необходимо учитывать, если мы хотим получить адекватную картину физического процесса.
площади сечения трубопровода невелики и на глаз незаметны, однако оказывается, что те и другие необходимо учитывать, если мы хотим получить адекватную картину физического процесса.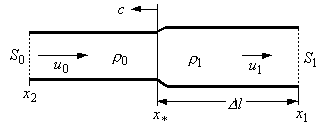
 массы жидкости на этом участке равно, с одной стороны,
массы жидкости на этом участке равно, с одной стороны,  , с другой –
, с другой –  , где
, где  интервал времени, за который волна возмущения распространилась на расстояние
интервал времени, за который волна возмущения распространилась на расстояние 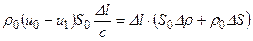
 . (4.1)
. (4.1) и
и  плотности жидкости и площади поперечного сечения трубопровода, соответственно, при увеличении давления на величину
плотности жидкости и площади поперечного сечения трубопровода, соответственно, при увеличении давления на величину  .
. или
или  , (4.2)
, (4.2) ,
,  – модуль упругости жидкости (Па). Среднее значение модуля
– модуль упругости жидкости (Па). Среднее значение модуля  Па.
Па.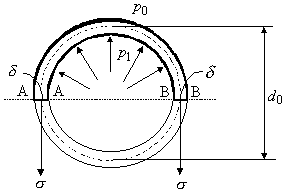
 и окружных напряжений
и окружных напряжений  , возникающих в металле трубы. Условия равновесия имеют вид:
, возникающих в металле трубы. Условия равновесия имеют вид: , (*)
, (*) толщина стенки. С другой стороны, закон упругости Гука, примененный к деформированному срединному волокну (на рис.18 оно обозначено пунктирной линией), дает соотношение:
толщина стенки. С другой стороны, закон упругости Гука, примененный к деформированному срединному волокну (на рис.18 оно обозначено пунктирной линией), дает соотношение: . (**)
. (**) модуль Юнга материала трубы (для стали
модуль Юнга материала трубы (для стали  Па), d1 – длина срединного волокна.
Па), d1 – длина срединного волокна. диаметра трубы в зависимости от разности
диаметра трубы в зависимости от разности  внутреннего и внешнего давлений:
внутреннего и внешнего давлений: . (4.3)
. (4.3) - диаметр срединного волокна трубы. Из (4.3) следует, в частности, искомая формула для относительного изменения
- диаметр срединного волокна трубы. Из (4.3) следует, в частности, искомая формула для относительного изменения  площади поперечного сечения трубопровода:
площади поперечного сечения трубопровода: или
или  . (4.4)
. (4.4) , (4.5)
, (4.5) , или с точностью до малых более высокого порядка:
, или с точностью до малых более высокого порядка:  .
. , где
, где  . Отсюда получаем формулу:
. Отсюда получаем формулу: ,
, вызывает повышение давления, а ускорение потока
вызывает повышение давления, а ускорение потока  – понижение давления.
– понижение давления. . (4.6)
. (4.6)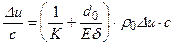
 , (4.7)
, (4.7) кг/м3,
кг/м3,  Па) по нефтепроводу
Па) по нефтепроводу  мм,
мм,  мм,
мм,  Па).
Па). м.
м. м/с.
м/с. мм,
мм,  мм,
мм,  м.
м. м/с.
м/с. Па или
Па или  атм.
атм. , что равносильно высокому давлению
, что равносильно высокому давлению  . При отражении волны гидравлического удара от закрытого сечения трубопровода или тупикового отвода амплитуда
. При отражении волны гидравлического удара от закрытого сечения трубопровода или тупикового отвода амплитуда  кг/м3,
кг/м3,  мм,
мм,  м.
м. м/с.
м/с. м/с.
м/с. Па или
Па или  атм.
атм. мм,
мм, 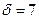 мм,
мм,  закачки нефти в трубопровод:
закачки нефти в трубопровод: м.
м. м/с.
м/с. м/с.
м/с. Па или
Па или  атм.
атм. мм,
мм,  м/с.
м/с. м/с.
м/с. Па или
Па или  атм.
атм.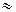 15 атм., то нефть за задвижкой может вскипеть, поскольку давление в ней снизится до упругости насыщенных паров. В этом случае за задвижкой образуется парогазовая полость.
15 атм., то нефть за задвижкой может вскипеть, поскольку давление в ней снизится до упругости насыщенных паров. В этом случае за задвижкой образуется парогазовая полость.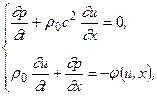 (4.8)
(4.8) . Это система двух дифференциальных уравнений с частными производными, используемых для расчета двух неизвестных функций
. Это система двух дифференциальных уравнений с частными производными, используемых для расчета двух неизвестных функций  и
и  .
. .
. .
. рассмотреть прямые линии, которые определяются уравнениями
рассмотреть прямые линии, которые определяются уравнениями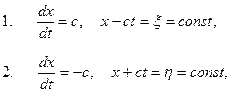
 :
: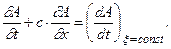
 ). Аналогично
). Аналогично ,
, ).
).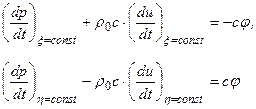
 (4.9)
(4.9)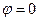 , то правые части уравнений в (4.9) равны нулю. Это означает, что вдоль характеристики положительного наклона (
, то правые части уравнений в (4.9) равны нулю. Это означает, что вдоль характеристики положительного наклона (  ) сохраняется величина
) сохраняется величина  , а вдоль характеристики отрицательного наклона (
, а вдоль характеристики отрицательного наклона (  ) сохраняется величина
) сохраняется величина  . Величины
. Величины  и
и  называются инвариантами Римана. Итак, при
называются инвариантами Римана. Итак, при  величины
величины  (в частности,
(в частности,  ) в трубопроводе известно распределение давлений и скоростей течения. Т.е. известны функции
) в трубопроводе известно распределение давлений и скоростей течения. Т.е. известны функции 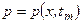 и
и  . Разработаем метод для расчета значений этих функций в следующий момент времени
. Разработаем метод для расчета значений этих функций в следующий момент времени  , отстоящий от данного на величину
, отстоящий от данного на величину  . Рассмотрим на плоскости переменных
. Рассмотрим на плоскости переменных  по координате и
по координате и  по времени (рис.19).
по времени (рис.19).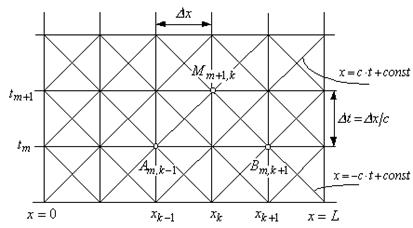
 и
и  положительного и отрицательного наклонов, соответственно. Непрерывное распределение искомых функций
положительного и отрицательного наклонов, соответственно. Непрерывное распределение искомых функций  и
и  сеточных функций в узлах построенной сетки. Предположим, что все значения
сеточных функций в узлах построенной сетки. Предположим, что все значения  и
и  известны в каком-нибудь временном слое
известны в каком-нибудь временном слое  и требуется найти значения сеточной функции при
и требуется найти значения сеточной функции при  , т.е.
, т.е.  и
и  . Покажем, как это сделать на примере произвольной точки
. Покажем, как это сделать на примере произвольной точки  .
.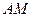 и
и  . Получим:
. Получим: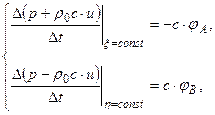
 ,
, .
. и скорости жидкости
и скорости жидкости  в точке
в точке  через известные величины этих параметров в точках
через известные величины этих параметров в точках  и
и  :
: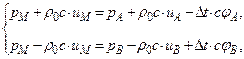
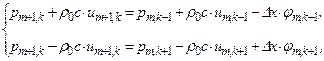
 и
и  – значения функции
– значения функции  , вычисленные по параметрам точек
, вычисленные по параметрам точек  через значения этих же параметров в момент времени
через значения этих же параметров в момент времени  (4.10)
(4.10) (
(  ) начиная с некоторого момента
) начиная с некоторого момента  и
и  ).
). ,
,  , определяющей участок трубопровода за исключением его начального (
, определяющей участок трубопровода за исключением его начального (  .
. и распределение напора
и распределение напора  , где
, где  – напор в начале рассматриваемого участка, а
– напор в начале рассматриваемого участка, а  – гидравлический уклон.
– гидравлический уклон.  , где
, где  – напор в конце участка. Тогда начальные условия для расчета нестационарного режима можно взять следующими:
– напор в конце участка. Тогда начальные условия для расчета нестационарного режима можно взять следующими: = const,
= const, 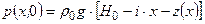
 ;
;  , (4.11)
, (4.11) ;
;  ;
;  ;
;  (
(  число частей, на которое разбивают участок трубопровода:
число частей, на которое разбивают участок трубопровода:  );
); 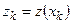 .
. В левое сечение (
В левое сечение (  и
и  в точках
в точках  левой границы необходимо иметь еще одну связь (алгебраическую или дифференциальную) между этими параметрами. В простейшем, но практически важном случае, такой связью может быть
левой границы необходимо иметь еще одну связь (алгебраическую или дифференциальную) между этими параметрами. В простейшем, но практически важном случае, такой связью может быть  характеристика перекачивающей станции, которая может быть представлена связью давления
характеристика перекачивающей станции, которая может быть представлена связью давления  в линии нагнетания и скорости
в линии нагнетания и скорости  перекачки:
перекачки:  нефтеперекачивающей станции, после того как на ней произошло то или иное изменение. Например, первоначально станция работала с одним набором нефтеперекачивающих агрегатов. Этому режиму соответствовало начальное состояние (4.11). А, начиная с момента времени
нефтеперекачивающей станции, после того как на ней произошло то или иное изменение. Например, первоначально станция работала с одним набором нефтеперекачивающих агрегатов. Этому режиму соответствовало начальное состояние (4.11). А, начиная с момента времени  , и т.д. Рис.20 поясняет систему алгебраических уравнений, которая служит для моделирования левого краевого условия:
, и т.д. Рис.20 поясняет систему алгебраических уравнений, которая служит для моделирования левого краевого условия: (4.12)
(4.12)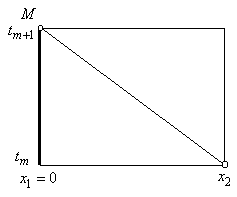
 давление в линии всасывания.
давление в линии всасывания. и
и  в точках
в точках  правой границы участка необходимо иметь еще одну связь (алгебраическую или дифференциальную) между этими параметрами. В частности, такая связь может быть представлена зависимостью
правой границы участка необходимо иметь еще одну связь (алгебраическую или дифференциальную) между этими параметрами. В частности, такая связь может быть представлена зависимостью  давления от скорости (расхода) в конце участка. В более простом случае в конце участка можно задать давление
давления от скорости (расхода) в конце участка. В более простом случае в конце участка можно задать давление  или скорость (расход)
или скорость (расход)  течения. Рис.21 поясняет систему алгебраических уравнений, которая служит для моделирования правого краевого условия:
течения. Рис.21 поясняет систему алгебраических уравнений, которая служит для моделирования правого краевого условия: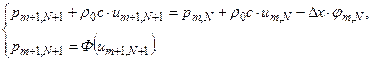 (4.13)
(4.13)