Линейная функция. Уравнение прямой. Парабола
Линейная функция  называется также линейной зависимостью или линейной регрессией. Уравнение называется также линейной зависимостью или линейной регрессией. Уравнение  подчёркивает, что y зависит от x, а не наоборот. Уравнение подчёркивает, что y зависит от x, а не наоборот. Уравнение  , напротив, указывает на равноправие переменных и применяется, когда линейная комбинация образует новую величину, например, производственные затраты. , напротив, указывает на равноправие переменных и применяется, когда линейная комбинация образует новую величину, например, производственные затраты.
Любая линия (не только прямая) пересекает ось абсцисс (ось OX), когда 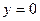 , а ось ординат (ось OY) – если , а ось ординат (ось OY) – если 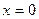 . Поэтому для поиска точек пересечения линии с системой координат подставляем эти значения по очереди в уравнение линии, находим другую координату и тем самым – точку пересечения. . Поэтому для поиска точек пересечения линии с системой координат подставляем эти значения по очереди в уравнение линии, находим другую координату и тем самым – точку пересечения.
С точки зрения математического анализа запись  точнее. Принятая форма записи точнее. Принятая форма записи  связана с традициями аналитической геометрии. связана с традициями аналитической геометрии.
ЛФ1. Отметьтеточки в декартовой системе координат:
1)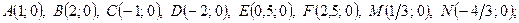
2)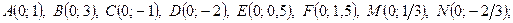
3)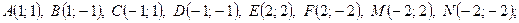
4)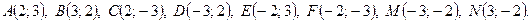
ЛФ2.Постройте прямые, параллельные осям координат:
1) а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  ; д) ; д)  ; е) ; е)  ; ;
2) а)  ; б) ; б) 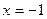 ; в) ; в)  ; г) ; г) 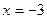 ; д) ; д)  ; е) ; е)  . .
Как выглядят прямые 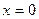 и и 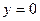 ? ?
ЛФ3.Постройте прямые, определив точки пересечения с осями координат:
1) а)  ; б) ; б)  ; в) ; в)  ; г) ; г) 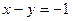 ; ;
2) а)  ; б) ; б)  ; в) ; в) 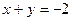 ; г) ; г)  ; ;
3) а)  ; б) ; б) 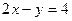 ; в) ; в)  ; г) ; г)  ; ;
4) а)  ; б) ; б) 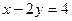 ; в) ; в)  ; г) ; г) 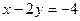 ; ;
5) а)  ; б) ; б) 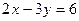 ; в) ; в)  ; г) ; г) 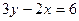 ; ;
6) а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  . .
Пример 1. Построим прямую  . .
Если 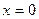 , то , то  , откуда , откуда  и соответственно и соответственно  . Значит, прямая пересекает ось OY (на которой . Значит, прямая пересекает ось OY (на которой 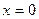 ) в точке ) в точке  . .
Если же 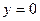 , то , то  , откуда , откуда  . Поэтому прямая пересекает ось OX (на которой . Поэтому прямая пересекает ось OX (на которой 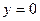 ) в точке ) в точке  . .
Отмечаем на оси OX точку  , на оси OY точку , на оси OY точку  и проводим прямую, проходящую через эти точки. и проводим прямую, проходящую через эти точки.
Пример 2. Построим прямую  : :
а) если 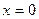 , то , то  , откуда , откуда  и и 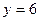 ; ;
б) если 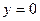 , то , то 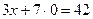 , откуда , откуда  и и 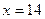 . .
Отмечаем на оси OX точку 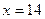 , на оси OY точку , на оси OY точку 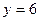 , и проводим прямую, проходящую через точки. , и проводим прямую, проходящую через точки.
ЛФ4.Постройте прямые, заданные уравнением с угловым коэффициентом:
1) а)  ; б) ; б) 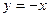 ; в) ; в)  ; г) ; г)  ; д) ; д)  ; ;
2) а) 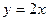 ; б) ; б)  ; в) ; в)  ; г) ; г) 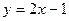 ; д) ; д)  ; ;
3) а)  ; б) ; б)  ; в) ; в) 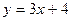 ; г) ; г)  ; д) ; д)  ; ;
4) а)  ; б) ; б)  ; в) ; в) 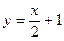 ; г) ; г)  ; д) ; д)  . .
Пример 3. Построим прямую  : :
а) пусть 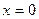 , тогда , тогда 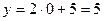 . Отмечаем точку . Отмечаем точку  ; ;
б) пусть 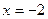 , тогда , тогда  . Отмечаем точку . Отмечаем точку 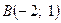 . .
Прямая проходит через А и В (и продолжается в обе стороны).
Замечание. При слишком близких значениях x прямая получится неточно. Не следует также брать x, при которых получается большое (по модулю) значение y.
ЛФ5.Постройте прямые, обращая внимание на зависимость расположения прямой от знака и величины коэффициентов:
1) а) 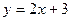 ; б) ; б)  ; в) ; в) 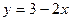 ; г) ; г) 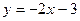 ; ;
д)  ; e) ; e) 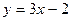 ; ж) ; ж)  ; з) ; з)  ; ;
2) а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  ; ;
д)  ; e) ; e)  ; ж) ; ж)  ; з) ; з)  ; ;
3) а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  ; ;
д)  ; e) ; e) 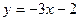 ; ж) ; ж)  ; з) ; з)  ; ;
4) а) 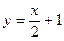 ; б) ; б)  ; в) ; в)  ; г) ; г)  ; ;
д) 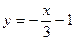 ; e) ; e)  ; ж) ; ж) 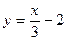 ; з) ; з) 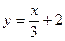 . .
ЛФ6.Постройте параболы любым способом:
1) а)  ; б) ; б) 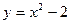 ; в) ; в)  ; г) ; г)  ; ;
д)  ; e) ; e)  ; ж) ; ж)  ; з) ; з)  ; ;
2) а)  ; б) ; б) 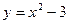 ; в) ; в) 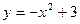 ; г) ; г)  ; ;
д)  ; e) ; e)  ; ж) ; ж)  ; з) ; з)  ; ;
3) а)  ; б) ; б) 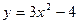 ; в) ; в)  ; г) ; г)  ; ;
д)  ; e) ; e) 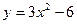 ; ж) ; ж) 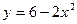 ; з) ; з)  ; ;
4) а) 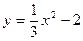 ; б) ; б)  ; в) ; в)  ; г) ; г)  ; ;
д)  ; e) ; e)  ; ж) ; ж)  ; з) ; з)  . .
Пример 4. Построим параболу  . .
Если 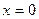 , то , то  . Парабола пересекает ось OY в точке . Парабола пересекает ось OY в точке  . .
Чтобы найти точки пересечения с осью OX, решаем уравнение  , получаем точки , получаем точки  и и  . .
Перед квадратом стоит знак «–». Значит, ветви направлены вниз.
В уравнении отсутствует линейное слагаемое px, поэтому вершина находится на оси OY. Общий вид параболы дан на рисунке 1. Ось OY проходит через точку 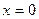 . .
|  Рисунок 1 – Парабола
Рисунок 1 – Парабола 
| ЛФ7.Постройте параболы, указав вершину и точки пересечения с осями координат (если такие точки есть):
1) а)  ; б) ; б)  ; в) ; в) 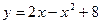 ; ;
г)  д) д)  ; е) ; е)  ; ;
2) а)  ; б) ; б)  ; в) ; в)  ; ;
г)  д) д)  ; е) ; е)  ; ;
3) а)  ; б) ; б)  ; в) ; в)  ; ;
г)  д) д)  ; е) ; е)  ; ;
4) а)  ; б) ; б)  ; в) ; в)  ; ;
г)  д) д)  ; е) ; е)  . .
Пример 5. Построим параболу 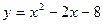 . .
Пусть 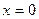 , тогда , тогда  . Парабола пересекает ось OY в точке . Парабола пересекает ось OY в точке  . .
Решим уравнение  . Получим точки . Получим точки  и и  . В них парабола пересекает ось OX. . В них парабола пересекает ось OX.
Когда парабола задана уравнением  , её вершина находится по формуле , её вершина находится по формуле  . В нашем случае . В нашем случае  , поэтому , поэтому  .
Соответственно, .
Соответственно, 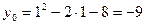 , и вершина – в точке , и вершина – в точке  .
Ветви идут вверх – перед квадратом в уравнении стоит знак «+». Ось OY проходит через .
Ветви идут вверх – перед квадратом в уравнении стоит знак «+». Ось OY проходит через 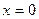 (рисунок 2). (рисунок 2).
|  Рисунок 2 – Парабола
Рисунок 2 – Парабола 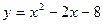
| Пример 6. Построим параболу  . .
Ветви направлены по горизонтали, поскольку x квадратично зависит от y. При этом перед квадратом в уравнении стоит знак «+» и ветви идут в положительном направлении – вправо.
Пусть 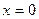 , тогда , тогда 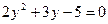 . Решение уравнения – точки . Решение уравнения – точки  и и  , в них парабола пересекает ось OY. , в них парабола пересекает ось OY.
Если 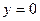 , то , то  и парабола пересекает ось OX в и парабола пересекает ось OX в  . .
Вершину находим по формуле  при при 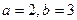 , поэтому , поэтому  .
При этом .
При этом  .
Вершина параболы находится в точке .
Вершина параболы находится в точке  (рисунок 3). (рисунок 3).
|  Рисунок 3 – Парабола
Рисунок 3 – Парабола 
|
Элементарные преобразования графиков
Пусть на некотором промежутке (интервале или отрезке) построенграфик функции 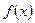 . Тогда на основе этого графика: . Тогда на основе этого графика:
1)а) график функции  получается сдвигом вправо на p единиц; получается сдвигом вправо на p единиц;
б) график функции  получается сдвигом влево на p единиц; получается сдвигом влево на p единиц;
в) график функции  получается сдвигом вверх на P единиц; получается сдвигом вверх на P единиц;
г) график функции  получается сдвигом вниз на P единиц. получается сдвигом вниз на P единиц.
Эти преобразования называются сдвигом графика;
2) а) график функции  получается сжатием в k раз вдоль оси ОХ получается сжатием в k раз вдоль оси ОХ
( в k раз приближается к оси OY);
б) график функции  получается растяжением в K раз вдоль оси OY получается растяжением в K раз вдоль оси OY
( в K раз отдаляется от оси ОХ).
Эти преобразования называются растяжением графика;
Кроме того,
а) график функции  получается отражением от оси OX; получается отражением от оси OX;
б) график функции  получается отражением части, лежащей ниже оси ОХ, относительно этой оси. Затем график под осью ОХ удаляется. Часть, лежащая выше оси OX, не меняется. получается отражением части, лежащей ниже оси ОХ, относительно этой оси. Затем график под осью ОХ удаляется. Часть, лежащая выше оси OX, не меняется.
Область определения функции (если таковой областью не служит вся числовая ось) меняется в случаях 1а, 1б и 2а; область значений – в остальных случаях.
ЭП1. Постройте график функции  . При помощи элементарных преобразований постройте графики функций . При помощи элементарных преобразований постройте графики функций  . .
1)  ; ;
а)  ; б) ; б)  ; в) ; в)  ; ;
г)  ; д) ; д)  ; е) ; е)  ; ;
ж)  ; з) ; з)  ; и) ; и) 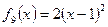 ; ;
к)  ; л) ; л)  ; м) ; м)  ; ;
2) 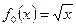 ; ;
а)  ; б) ; б)  ; в) ; в)  ; ;
г)  ; д) ; д)  ; е) ; е) 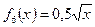 ; ;
ж)  ; з) ; з) 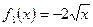 ; и) ; и) 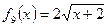 ; ;
к)  ; л) ; л)  ; м) ; м) 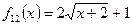 ; ;
3) 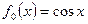 ; ;
а)  ; б) ; б)  ; в) ; в)  ; ;
г)  ; д) ; д)  ; е) ; е)  ; ;
ж)  ; з) ; з) 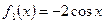 ; и) ; и)  ; ;
к)  ; л) ; л)  ; м) ; м)  ; ;
4)  (правая ветвь); (правая ветвь);
а)  ; б) ; б)  ; в) ; в)  ; ;
г)  ; д) ; д)  ; е) ; е)  ; ;
ж)  ; з) ; з)  ; и) ; и)  ; ;
к) 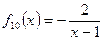 ; л) ; л)  ; м) ; м)  . .
Замечание 1. График функции  строится на полуоси строится на полуоси  , поскольку , поскольку  не определено. Соответственно строятся и все последующие графики, например не определено. Соответственно строятся и все последующие графики, например  – на – на  , ,  – на – на  , и т.п. , и т.п.
ЭП2. Постройте графики при помощи элементарных преобразований:
1) а)  ; б) ; б) 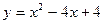 ; в) ; в) 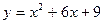 ; ;
2) а) 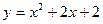 ; б) ; б)  ; в) ; в)  ; ;
3) а)  ; б) ; б)  ; в) ; в)  ; ;
4) а)  ; б) ; б)  ; в) ; в) 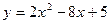 ; ;
5) а)  ; б) ; б)  ; в) ; в)  ; ;
6) а)  ; б) ; б)  ; в) ; в)  ; ;
7) а)  ; б) ; б)  ; в) ; в)  . .
Пример 1. Пусть  . Поскольку . Поскольку  и при этом и при этом  , то , то  , или , или  . Строим параболу . Строим параболу  , а затем , а затем
а) смещаем на 1 ед. влево – теперь вершина не в точке  , а в точке , а в точке  . Получаем график функции . Получаем график функции  ; ;
б) растягиваем в 2 раза по вертикали. Точка 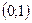 превращается в превращается в  , точка , точка 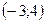 – в точку – в точку  , и т.д. Получается график функции , и т.д. Получается график функции 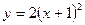 ; ;
в) поднимаем график на 3 ед. Вершина оказывается в точке  . .
ЭП3.Постройте схематичные графики функций
а) при помощи асимптот и точек пересечения с осями координат;
б) при помощи элементарных преобразований графика функции  : :
1) а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  ; д) ; д)  ; ;
2) а)  ; б) ; б)  ; в) ; в)  ; г) ; г) 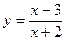 ; д) ; д)  ; ;
3) а)  ; б) ; б)  ; в) ; в)  ; г) ; г) 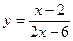 ; д) ; д) 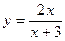 ; ;
4) а) 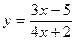 ; б) ; б)  ; в) ; в)  ; г) ; г)  ; д) ; д)  . .
Пример 2. Построим график функции  . .
1-й способ. В точке 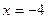 знаменатель обращается в 0, а при знаменатель обращается в 0, а при  значения очень велики. Это означает, что значения очень велики. Это означает, что 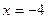 – не только координаты точки, которую нельзя подставить, но и уравнение вертикальной асимптоты. – не только координаты точки, которую нельзя подставить, но и уравнение вертикальной асимптоты.
Горизонтальная асимптота – это прямая, к которой приближается график при очень больших x (при 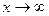 ). Легко заметить, что при больших значениях x дробь ). Легко заметить, что при больших значениях x дробь  . Значит, . Значит,  – уравнение горизонтальной асимптоты. – уравнение горизонтальной асимптоты.
График пересекает ось OY, когда 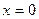 , при этом , при этом  . .
График пересекает ось OX, когда 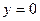 . Из уравнения . Из уравнения  находим, что находим, что 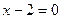 , и потому , и потому  . .
Итак, график пересекает ось OX в точке  , ось OY – в точке , ось OY – в точке 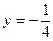 , уходит в бесконечность вдоль вертикальной прямой , уходит в бесконечность вдоль вертикальной прямой 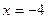 , а при удалении вправо и влево приближается к горизонтальной прямой , а при удалении вправо и влево приближается к горизонтальной прямой  . .
2-й способ. Чтобы построить график при помощи элементарных преобразований, функцию  следует привести к виду следует привести к виду  или к виду или к виду  , где , где  – некоторые числа. – некоторые числа.
Заметим, что  , и выделим в числителе часть, пропорциональную замеченной скобке , и выделим в числителе часть, пропорциональную замеченной скобке 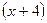 : :  , тогда , тогда  (сокращение на 2 во 2-й дроби случайно). Получили, что (сокращение на 2 во 2-й дроби случайно). Получили, что  , и тогда , и тогда  ; ;
а) строим график функции  ; ;
б) сдвигаем его на 4 ед. влево – график вытягивается по вертикали не вдоль оси OY, а вдоль прямой 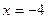 ; ;
в) отражаем график относительно оси OY – ветви «переворачиваются»;
г) поднимаем график на 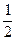 ед.– ветви вытягиваются вдоль прямой ед.– ветви вытягиваются вдоль прямой  . .
§ 3. Аналитическое задание функций
Функция  задана аналитически, если предложена некоторая формула, по которой для каждого конкретного аргумента x можно найти соответствующее значение y. В общем случае это зависимость задана аналитически, если предложена некоторая формула, по которой для каждого конкретного аргумента x можно найти соответствующее значение y. В общем случае это зависимость  , но если её можно свести к виду , но если её можно свести к виду  , то говорят, что функция задана в явном виде. , то говорят, что функция задана в явном виде.
Например,  – неявно заданная функция – неявно заданная функция  . В то же время . В то же время  – функция в явном виде. С другой стороны, можно вести речь о двузначной функции – функция в явном виде. С другой стороны, можно вести речь о двузначной функции  , определённой при , определённой при 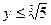 , поскольку для любого , поскольку для любого 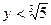 возможны 2 значения x (при возможны 2 значения x (при  функция функция  не определена, при не определена, при  получим получим 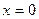 ). ).
Задача о поиске зависимости  на основе известной неявно заданной функции возникает, например, при решении дифференциальных уравнений или при построении графиков. Кроме того, необходимость выразить переменную x через переменную t, когда дана зависимость на основе известной неявно заданной функции возникает, например, при решении дифференциальных уравнений или при построении графиков. Кроме того, необходимость выразить переменную x через переменную t, когда дана зависимость  , появляется при интегрировании функций. , появляется при интегрировании функций.
АЗ1. Выразите y как функцию  . Найдите значение . Найдите значение  . Укажите область определения функции: . Укажите область определения функции:
1) а)  ; б) ; б)  ; в) ; в)  ; ;
г)  ; д) ; д)  ; е) ; е)  ; ;
2) а)  ; б) ; б) 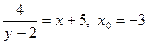 ; в) ; в)  ; ;
г)  ; д) ; д)  ; е) ; е)  ; ;
3) а) 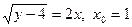 ; б) ; б)  ; в) ; в) 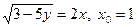 ; ;
4) а)  ; б) ; б)  ; в) ; в)  ; ;
5) а)  ; б) ; б)  ; в) ; в)  ; ;
6) а)  ; б) ; б)  ; в) ; в)  ; ;
г)  ; д) ; д)  ; е) ; е)  . .
Пример 1. Пусть  . Если . Если  и и  , то обратные величины также равны: , то обратные величины также равны:  , и , и 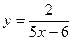 . Функция определена при . Функция определена при  . .
В точке 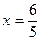 условие превращается в невозможное равенство условие превращается в невозможное равенство 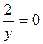 , а при вычислении , а при вычислении 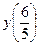 получаем деление на 0. Если же получаем деление на 0. Если же  , то , то  . .
Ответ: 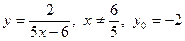 . .
Пример 2. Пусть  . Очевидно, . Очевидно, 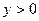 . Сам же логарифм может принимать любое значение (в отличие, например, от квадратного корня или синуса), поэтому ограничений на . Сам же логарифм может принимать любое значение (в отличие, например, от квадратного корня или синуса), поэтому ограничений на 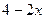 нет, и тогда x – любое число. нет, и тогда x – любое число.
По определению логарифма, 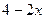 – это степень, в которую надо возвести 10, чтобы получить y. Таким образом, – это степень, в которую надо возвести 10, чтобы получить y. Таким образом,  , или , или  . .
Если  , то , то  . .
Ответ:  , ,  . .
Пример 3. Пусть 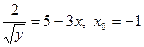 . Если . Если  существует, то существует, то  . Из условия видно, что . Из условия видно, что  . Значит, . Значит,  , и тогда , и тогда  (поскольку числитель (поскольку числитель  ). Поэтому ). Поэтому  . Отсюда . Отсюда  . .
По свойству пропорций можно поменять местами  и и 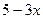 : :  . Возведём в квадрат . Возведём в квадрат  . Функция определена при . Функция определена при  , что не отражается на уже установленном ограничении , что не отражается на уже установленном ограничении  . .
В точке 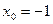 находим находим  . .
Ответ:  . .
Пример 4. В случае  замечаем, что в левой части условия есть замечаем, что в левой части условия есть  , но , но 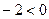 , и тогда дробь , и тогда дробь 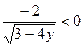 . Значит, в правой части . Значит, в правой части  , откуда , откуда  . .
Равенство  , равносильное начальному, возводим в квадрат: , равносильное начальному, возводим в квадрат:  , тогда , тогда 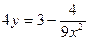 и и 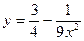 . .
То, что  , т.е. , т.е. 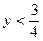 , учитывается формулой функции. В самом деле, дробь , учитывается формулой функции. В самом деле, дробь  , и при вычитании её из , и при вычитании её из  это число можно только уменьшить. это число можно только уменьшить.
В точке 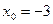 будет будет  . .
Ответ: 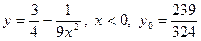 . .
Пример 5. Пусть  . Возведём в квадрат . Возведём в квадрат  , но учтём, что , но учтём, что  и и  , т.е. что , т.е. что  и и  . .
Из уравнения  выразим выразим  , тогда , тогда  и тем самым и тем самым 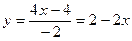 . Также находим . Также находим  . .
Ответ:  . .
Пример 6. Пусть  . Из условия видно, что . Из условия видно, что  и и  . Обратные величины также равны: . Обратные величины также равны: 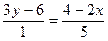 или или  . .
Переносим: 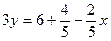 , выражаем , выражаем  , где , где  . .
Итак,  при при  . .
Кроме того,  . .
Ответ:  . .
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 называется также линейной зависимостью или линейной регрессией. Уравнение
называется также линейной зависимостью или линейной регрессией. Уравнение  , напротив, указывает на равноправие переменных и применяется, когда линейная комбинация образует новую величину, например, производственные затраты.
, напротив, указывает на равноправие переменных и применяется, когда линейная комбинация образует новую величину, например, производственные затраты.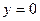 , а ось ординат (ось OY) – если
, а ось ординат (ось OY) – если 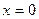 . Поэтому для поиска точек пересечения линии с системой координат подставляем эти значения по очереди в уравнение линии, находим другую координату и тем самым – точку пересечения.
. Поэтому для поиска точек пересечения линии с системой координат подставляем эти значения по очереди в уравнение линии, находим другую координату и тем самым – точку пересечения. точнее. Принятая форма записи
точнее. Принятая форма записи 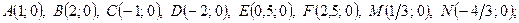
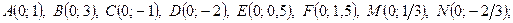
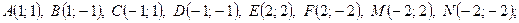
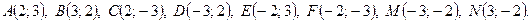
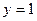 ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  ;
;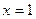 ; б)
; б) 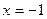 ; в)
; в)  ; г)
; г) 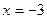 ; д)
; д)  ; е)
; е)  .
. ; б)
; б)  ; в)
; в)  ; г)
; г) 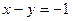 ;
; ; б)
; б)  ; в)
; в) 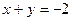 ; г)
; г)  ;
; ; б)
; б) 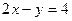 ; в)
; в)  ; г)
; г)  ;
; ; б)
; б) 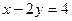 ; в)
; в)  ; г)
; г) 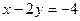 ;
; ; б)
; б) 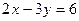 ; в)
; в)  ; г)
; г) 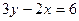 ;
; ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. .
. , откуда
, откуда  и соответственно
и соответственно  . Значит, прямая пересекает ось OY (на которой
. Значит, прямая пересекает ось OY (на которой  , откуда
, откуда  . Поэтому прямая пересекает ось OX (на которой
. Поэтому прямая пересекает ось OX (на которой  :
: , откуда
, откуда  и
и 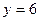 ;
;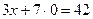 , откуда
, откуда  и
и 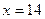 .
. ; б)
; б) 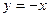 ; в)
; в)  ; г)
; г)  ; д)
; д)  ;
;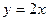 ; б)
; б)  ; в)
; в)  ; г)
; г) 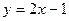 ; д)
; д)  ;
; ; б)
; б)  ; в)
; в) 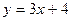 ; г)
; г)  ; д)
; д)  ;
; ; б)
; б)  ; в)
; в) 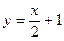 ; г)
; г)  ; д)
; д)  .
. :
: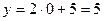 . Отмечаем точку
. Отмечаем точку  ;
;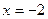 , тогда
, тогда  . Отмечаем точку
. Отмечаем точку 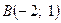 .
.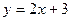 ; б)
; б)  ; в)
; в) 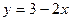 ; г)
; г) 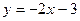 ;
; ; e)
; e) 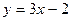 ; ж)
; ж)  ; з)
; з)  ;
; ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
; ; e)
; e)  ; ж)
; ж)  ; з)
; з)  ;
; ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
; ; e)
; e) 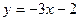 ; ж)
; ж)  ; з)
; з)  ;
; ; в)
; в)  ; г)
; г)  ;
;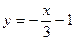 ; e)
; e)  ; ж)
; ж) 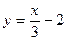 ; з)
; з) 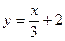 .
. ; б)
; б) 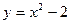 ; в)
; в)  ; г)
; г)  ;
; ; e)
; e)  ; ж)
; ж)  ; з)
; з)  ;
; ; б)
; б) 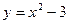 ; в)
; в) 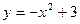 ; г)
; г)  ;
; ; e)
; e)  ; ж)
; ж)  ; з)
; з)  ;
; ; б)
; б) 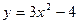 ; в)
; в)  ; г)
; г)  ;
; ; e)
; e) 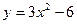 ; ж)
; ж) 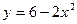 ; з)
; з)  ;
;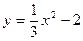 ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
; ; e)
; e)  ; ж)
; ж)  ; з)
; з)  .
. .
. . Парабола пересекает ось OY в точке
. Парабола пересекает ось OY в точке  .
. , получаем точки
, получаем точки  и
и  .
. Рисунок 1 – Парабола
Рисунок 1 – Парабола  ; б)
; б)  ; в)
; в) 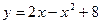 ;
; д)
д)  ; е)
; е)  ;
; ; б)
; б)  ; в)
; в)  ;
; д)
д)  ; е)
; е)  ;
; ; б)
; б)  ; в)
; в)  ;
; д)
д)  ; е)
; е)  ;
; ; б)
; б)  ; в)
; в)  ;
; д)
д)  ; е)
; е)  .
.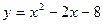 .
. . Парабола пересекает ось OY в точке
. Парабола пересекает ось OY в точке  .
. . Получим точки
. Получим точки  . В них парабола пересекает ось OX.
. В них парабола пересекает ось OX. , её вершина находится по формуле
, её вершина находится по формуле  . В нашем случае
. В нашем случае  , поэтому
, поэтому  .
Соответственно,
.
Соответственно, 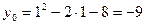 , и вершина – в точке
, и вершина – в точке  .
Ветви идут вверх – перед квадратом в уравнении стоит знак «+». Ось OY проходит через
.
Ветви идут вверх – перед квадратом в уравнении стоит знак «+». Ось OY проходит через  Рисунок 2 – Парабола
Рисунок 2 – Парабола  .
.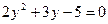 . Решение уравнения – точки
. Решение уравнения – точки  и
и  , в них парабола пересекает ось OY.
, в них парабола пересекает ось OY. и парабола пересекает ось OX в
и парабола пересекает ось OX в  .
. при
при 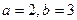 , поэтому
, поэтому  .
При этом
.
При этом  .
Вершина параболы находится в точке
.
Вершина параболы находится в точке  (рисунок 3).
(рисунок 3).
 Рисунок 3 – Парабола
Рисунок 3 – Парабола 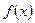 . Тогда на основе этого графика:
. Тогда на основе этого графика: получается сдвигом вправо на p единиц;
получается сдвигом вправо на p единиц; получается сдвигом влево на p единиц;
получается сдвигом влево на p единиц; получается сдвигом вверх на P единиц;
получается сдвигом вверх на P единиц; получается сдвигом вниз на P единиц.
получается сдвигом вниз на P единиц. получается сжатием в k раз вдоль оси ОХ
получается сжатием в k раз вдоль оси ОХ получается растяжением в K раз вдоль оси OY
получается растяжением в K раз вдоль оси OY получается отражением от оси OX;
получается отражением от оси OX; получается отражением части, лежащей ниже оси ОХ, относительно этой оси. Затем график под осью ОХ удаляется. Часть, лежащая выше оси OX, не меняется.
получается отражением части, лежащей ниже оси ОХ, относительно этой оси. Затем график под осью ОХ удаляется. Часть, лежащая выше оси OX, не меняется. . При помощи элементарных преобразований постройте графики функций
. При помощи элементарных преобразований постройте графики функций  .
. ;
; ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  ; е)
; е)  ;
; ; з)
; з)  ; и)
; и) 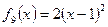 ;
; ; л)
; л)  ; м)
; м)  ;
;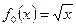 ;
; ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  ; е)
; е) 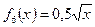 ;
; ; з)
; з) 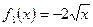 ; и)
; и) 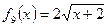 ;
; ; л)
; л)  ; м)
; м) 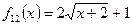 ;
;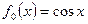 ;
; ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  ; е)
; е)  ;
; ; з)
; з) 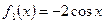 ; и)
; и)  ;
; ; л)
; л)  ; м)
; м)  ;
; (правая ветвь);
(правая ветвь); ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  ; е)
; е)  ;
; ; з)
; з)  ; и)
; и)  ;
;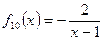 ; л)
; л)  ; м)
; м)  .
. , поскольку
, поскольку  не определено. Соответственно строятся и все последующие графики, например
не определено. Соответственно строятся и все последующие графики, например  – на
– на  ,
,  – на
– на  , и т.п.
, и т.п. ; б)
; б) 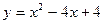 ; в)
; в) 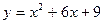 ;
;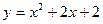 ; б)
; б)  ; в)
; в)  ;
; ; б)
; б)  ; в)
; в)  ;
; ; б)
; б)  ; в)
; в) 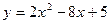 ;
; ; б)
; б)  ; в)
; в)  ;
; ; б)
; б)  ; в)
; в)  ;
; ; б)
; б)  ; в)
; в)  .
. и при этом
и при этом  , то
, то  , или
, или  . Строим параболу
. Строим параболу  , а затем
, а затем , а в точке
, а в точке  . Получаем график функции
. Получаем график функции  ;
;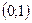 превращается в
превращается в  , точка
, точка 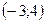 – в точку
– в точку  , и т.д. Получается график функции
, и т.д. Получается график функции 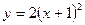 ;
; .
. :
: ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ;
; ; б)
; б)  ; в)
; в)  ; г)
; г) 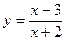 ; д)
; д)  ;
; ; б)
; б)  ; в)
; в)  ; г)
; г) 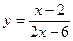 ; д)
; д) 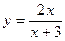 ;
;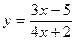 ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  .
. .
.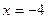 знаменатель обращается в 0, а при
знаменатель обращается в 0, а при  значения очень велики. Это означает, что
значения очень велики. Это означает, что 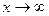 ). Легко заметить, что при больших значениях x дробь
). Легко заметить, что при больших значениях x дробь  . Значит,
. Значит,  – уравнение горизонтальной асимптоты.
– уравнение горизонтальной асимптоты. .
. находим, что
находим, что 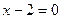 , и потому
, и потому 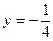 , уходит в бесконечность вдоль вертикальной прямой
, уходит в бесконечность вдоль вертикальной прямой  или к виду
или к виду  , где
, где  – некоторые числа.
– некоторые числа. , и выделим в числителе часть, пропорциональную замеченной скобке
, и выделим в числителе часть, пропорциональную замеченной скобке 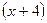 :
:  , тогда
, тогда  (сокращение на 2 во 2-й дроби случайно). Получили, что
(сокращение на 2 во 2-й дроби случайно). Получили, что  , и тогда
, и тогда  ;
; ;
;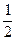 ед.– ветви вытягиваются вдоль прямой
ед.– ветви вытягиваются вдоль прямой  задана аналитически, если предложена некоторая формула, по которой для каждого конкретного аргумента x можно найти соответствующее значение y. В общем случае это зависимость
задана аналитически, если предложена некоторая формула, по которой для каждого конкретного аргумента x можно найти соответствующее значение y. В общем случае это зависимость  , но если её можно свести к виду
, но если её можно свести к виду  , то говорят, что функция задана в явном виде.
, то говорят, что функция задана в явном виде. – неявно заданная функция
– неявно заданная функция  – функция в явном виде. С другой стороны, можно вести речь о двузначной функции
– функция в явном виде. С другой стороны, можно вести речь о двузначной функции  , определённой при
, определённой при 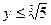 , поскольку для любого
, поскольку для любого 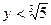 возможны 2 значения x (при
возможны 2 значения x (при  функция
функция  не определена, при
не определена, при  получим
получим  , появляется при интегрировании функций.
, появляется при интегрировании функций. . Укажите область определения функции:
. Укажите область определения функции: ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  ; е)
; е)  ;
; ; б)
; б) 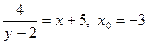 ; в)
; в)  ;
; ; д)
; д)  ; е)
; е)  ;
;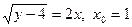 ; б)
; б)  ; в)
; в) 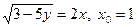 ;
; ; б)
; б)  ; в)
; в)  ;
; ; б)
; б)  ; в)
; в)  ;
; ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  ; е)
; е)  .
. . Если
. Если  и
и  , то обратные величины также равны:
, то обратные величины также равны:  , и
, и 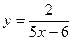 . Функция определена при
. Функция определена при  .
.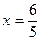 условие превращается в невозможное равенство
условие превращается в невозможное равенство 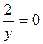 , а при вычислении
, а при вычислении 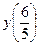 получаем деление на 0. Если же
получаем деление на 0. Если же  , то
, то  .
.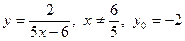 .
. . Очевидно,
. Очевидно, 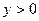 . Сам же логарифм может принимать любое значение (в отличие, например, от квадратного корня или синуса), поэтому ограничений на
. Сам же логарифм может принимать любое значение (в отличие, например, от квадратного корня или синуса), поэтому ограничений на 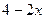 нет, и тогда x – любое число.
нет, и тогда x – любое число. , или
, или  .
. , то
, то  .
. .
.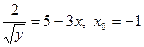 . Если
. Если  существует, то
существует, то  . Из условия видно, что
. Из условия видно, что  . Значит,
. Значит,  , и тогда
, и тогда  (поскольку числитель
(поскольку числитель  ). Поэтому
). Поэтому  . Отсюда
. Отсюда  .
.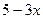 :
:  . Возведём в квадрат
. Возведём в квадрат  . Функция определена при
. Функция определена при  , что не отражается на уже установленном ограничении
, что не отражается на уже установленном ограничении 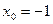 находим
находим  .
. .
. замечаем, что в левой части условия есть
замечаем, что в левой части условия есть  , но
, но 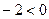 , и тогда дробь
, и тогда дробь 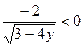 . Значит, в правой части
. Значит, в правой части  , откуда
, откуда  .
. , равносильное начальному, возводим в квадрат:
, равносильное начальному, возводим в квадрат:  , тогда
, тогда 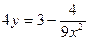 и
и 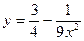 .
. , т.е.
, т.е. 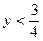 , учитывается формулой функции. В самом деле, дробь
, учитывается формулой функции. В самом деле, дробь  , и при вычитании её из
, и при вычитании её из  это число можно только уменьшить.
это число можно только уменьшить.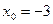 будет
будет  .
.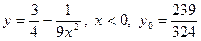 .
. . Возведём в квадрат
. Возведём в квадрат  , но учтём, что
, но учтём, что  и
и  , т.е. что
, т.е. что  и
и  .
. , тогда
, тогда  и тем самым
и тем самым 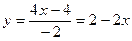 . Также находим
. Также находим  .
. .
. . Из условия видно, что
. Из условия видно, что  и
и  . Обратные величины также равны:
. Обратные величины также равны: 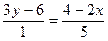 или
или  .
.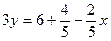 , выражаем
, выражаем  , где
, где  .
. при
при  .
. .
.