
|
|
Рекомендации по выполнению заданийОпд. ф. 08 гидрогазодинамика Методические указания к выполнению расчетно-графических работ
Направление 140100 Теплоэнергетика
Уфа 2008 УДК 378.147: 532 ББК 74. 58: 30.128 А 53
Рекомендовано к изданию методической комиссией факультета энергетики (протокол № от 2008 г.)
Составитель: профессор Алмаев Р.А.
Рецензент: профессор Дусыев В.М.
Ответственный за выпуск: заведующий кафедрой гидравлики профессор Алмаев Р.А.
г. Уфа, БГАУ, кафедра гидравлики
ВВЕДЕНИЕ Методические указания включают рекомендации по решению задач и выполнению расчетно-графических работ с использованием основных уравнений гидростатики и гидрогазодинамики по темам: "Сила давления жидкости на плоские и криволинейные поверхности", "Уравнение Бернулли для потока реальной жидкости", "Гидравлический расчет трубопроводов", «Одномерное движение газа». Приступая к выполнению расчетного задания, следует, используя учебную литературу, проработать соответствующий теоретический материал, уяснить общую методику расчета, физический смысл и условия применимости расчетных уравнений и формул. Решение должно иллюстрироваться расчетной схемой и сопровождаться краткими пояснениями. При этом необходимо использовать общепринятые обозначения физических величин и сокращения слов. Значения коэффициентов и табличных функций даются со ссылкой на литературный источник. Во избежание ошибок подстановка в формулу числовых значений величин выполняется в порядке ее написания и в одной системе единиц измерения (в системе СИ). Рекомендации по выполнению заданий 1.1 Задание по теме: "Сила давления жидкости на плоские и криволинейные поверхности". Условием задания предусмотрено решение двух задач. В первой задаче для заданной расчетной схемы требуется определить усилие для открытия плоского затвора, смонтированного в стенке резервуара или в водопроводящем канале. Затвор испытывает одно - или двухстороннее воздействие жидкости и может совершать поступательное движение в направляющих или поворотное движение относительно оси шарнира. Искомое усилие находится с учетом действующих на затвор внешних сил: давления жидкости, трения в направляющих, веса затвора. Расчет выполняется в следующем порядке: 1) Определяют величину силы давления жидкости на затвор: Р = рсw, (1.1) где рс - давление в центре тяжести рассматриваемой фигуры; w - площадь смоченной поверхности фигуры. Следует найти положение и глубину hс погружения центра тяжести затвора и по основному уравнению гидростатики определить давление рс. Расчет можно вести по абсолютным или избыточным давлениям в рассматриваемых точках. При абсолютном равновесии давление в произвольной точке объема однородной жидкости: рабс= ро+rgh , (1.2) где ро – абсолютное давление на свободной поверхности жидкости; r - плотность жидкости; g – ускорение свободного падения; h – глубина погружения рассматриваемой точки. 2) Определяют точку приложения силы давления Для вертикальной плоской фигуры заглубление точки приложения силы давления hд= hc+ (J0/hcw), (1.3) где hс - глубина погружения центра тяжести фигуры; J0- центральный момент инерции площади w. Координаты центра тяжести плоских фигур и моменты инерции J0 приведены в литературе [2,6]. Отсчет глубин hc и hд от уровня свободной поверхности. В случае наклонной плоской фигуры формула (1.3) записывается по продольным координатам ус центра тяжести фигуры и уд центра давления. При этом, очевидно, hc = усsina и hд = удsina, где a - угол наклона плоской фигуры к горизонту. При двухстороннем воздействии среды на затвор следует определить силы давления слева и справа, их равнодействующую и точку ее приложения. Для определения точки приложения равнодействующей составляется уравнение моментов сил. На расчетной схеме следует показать направление действия сил, глубины погружения точек приложения сил. 3) Определяют усилие, потребное для открытия затвора Для этого следует составить расчетную схему сил и записать уравнение равновесия или уравнение моментов сил, действующих на затвор. Во второй задаче рассматривается воздействие жидкости на криволинейную (цилиндрическую) поверхность. Требуется определить величину силы давления и точку ее приложения. Расчет выполняется в следующей последовательности: 1) Определяют горизонтальную составляющую силы давления: Рх = рсwz , (1.4) где рс - давление в центре тяжести вертикальной проекции криволинейной поверхности; wz - площадь этой проекции. Рассматриваемая криволинейная поверхность проектируется на вертикальную плоскость, находится центр тяжести полученной проекции и давление рс. В зависимости от условия задачи расчет ведется по абсолютному или избыточному давлению. Точка приложения силы Рх, как и в случае плоской поверхности, находится с использованием формулы (1.3). Величина силы Рх и положение центра давления могут быть найдены графо-аналитическим способом построением эпюры давления. 2) Определяют вертикальную составляющую силы давления: Рz = g Wт.д ,(1.5) где g - удельный вес жидкости; Wт.д - объем тела давления. Построение тела давления подробно рассмотрено в учебной литературе [1, 2, 4]. В случае цилиндрической поверхности его объем найдется как произведение площади поперечного сечения тела давления S т.д на ширину поверхности b, т.е. Wт.д. = S т.д b. Вертикальная составляющая силы давления Рz проходит через центр тяжести объема Wт.д. Если объем тела давления заполнен жидкостью, сила Рz положительна и направлена вниз; если объем тела давления не заполнен жидкостью (фиктивное тело давления), сила Рz отрицательна и направлена вверх. 3) Определяют равнодействующую силу и точку ее приложения. Величина силы: Р = Ö Рх2+ Рz2 (1.6) Направление силы (по углу j): tg j = Рz /Рх (1.7) Координаты точки приложения силы можно определить из уравнения окружности х2 + z2 = r2 . Контрольные вопросы 1) Как определяется величина силы давления жидкости на вертикальную (наклонную) плоскую поверхность? Запишите расчетную формулу, поясните смысл и определение величин. 2) Поясните определение точки приложения силы давления жидкости на плоскую поверхность аналитическим способом. 3) Как определяются величина силы давления и положение центра давления графо-аналитическим способом? 4) Поясните общую методику расчета силы давления жидкости на криволинейную поверхность. 5) Как определяется точка приложения силы давления жидкости на цилиндрическую поверхность? 1.2 Задание по теме: “Применение уравнения Бернулли. Расчет простых коротких трубопроводов”. В качестве задания определена схема гидравлической системы, в которой питание трубопровода жидкостью осуществляется напорным резервуаром или насосом. В зависимости от исходных данных следует решить одну из трех типовых задач гидравлического расчета простого трубопровода: определение напора Н (давления р), расхода Q или диаметра d. При решении задачи применяют уравнение Бернулли. Для установившегося плавно изменяющегося движения реальной жидкости уравнение Бернулли имеет вид (для двух произвольных сечений 1-1 и 2-2):
z1+
где z1, z2 – геометрические высоты сечений; р1, р2 – давления в сечениях;
h1-2 – потери напора между сечениями на преодоление гидравлических сопротивлений. С энергетической точки зрения члены уравнения Бернулли выражают различные виды удельной энергии жидкости (потенциальной и кинетической). Сумма z + Из уравнения Бернулли следует, что вдоль потока полный напор уменьшается вследствие гидравлических сопротивлений. Используя уравнение (1.8) для конкретной гидравлической схемы, можно получить расчетное выражение, которое связывает основные параметры движения жидкости в трубопроводе. Общая методика применения уравнения Бернулли: 1) На расчетной схеме намечают два сечения 1-1 и 2-2. Обычно сечения намечают на уровне свободной поверхности жидкости в резервуарах, в местах установки приборов для измерения давления и др. Нумерация сечений выполняется по ходу движения жидкости. 2) Проводят горизонтальную плоскость сравнения 0-0. Целесообразно провести плоскость через центр тяжести ниже расположенного сечения. 3) Записывают уравнение Бернулли в общем виде и с учетом выбранных сечений находят значения z, р и u. Давления в сечениях должны быть одинаковые по виду (абсолютные или избыточные). 4) Подставляют найденные значения z, р, u в исходное уравнение и решают его относительно напора Н (или давления p). Если в полученном уравнении число неизвестных два и более, следует привлечь дополнительные уравнения. Рекомендуется использовать уравнение баланса расхода Q = uw = const и выражение для потерь напора. Коэффициенты Кориолиса a1 и a2 исключают из числа неизвестных, задаваясь режимом движения жидкости. В большинстве практических случаев имеет место турбулентный режим, для которого можно принять a1,2»1. При решении задачи на определение напора по исходным данным находят последовательно скорость u, режим течения (по числу Rе), коэффициент гидравлического трения l и коэффициенты местных сопротивлений zм, потери напора. При определении расхода Q, полученное из уравнения Бернулли выражение для Н, дополняют уравнениями потерь напора и баланса расхода, а затем совместно решают систему уравнений относительно u. Численный расчет ведут методом последовательных приближений. В первом приближении задаются значением l = 0,02-0,03 или находят его без учета режима течения по известным эмпирическим формулам [1, 2, 5, 6, 7]. По найденной u определяют режим, уточняют l и скорость u. Задача на определение диаметра решается по уравнению напора Н методом подбора. Задаются рядом значений d (не менее 4-5) и вычисляют соответствующие значения Н. По результатам расчета строится график зависимости Н=¦(d), из которого по заданному Нзад находят искомое значение dиск. По результатам расчета необходимо построить график напоров. Для построения напорной и пьезометрической линий между сечениями 1-1 и 2-2 на трубопроводе дополнительно намечают ряд сечений (в характерных местах потока: в зоне расположения местных сопротивлений, на границах прямолинейных участков) и вычисляют для них полные (с учетом потерь напора) и пьезометрические напоры. Расчет напоров начинают с сечения 1-1. Рекомендуется вести расчет по избыточному давлению. Тогда Н1 = z1 + (ризб/rg) + ( График строится на миллиметровой бумаге в масштабе, обеспечивающем наглядность изображения. На числовой оси Н (в м) наносится равномерная шкала. Вычисленные значения полных и пьезометрических напоров откладывают вверх в виде отрезков от плоскости сравнения 0-0 и соединяют концы отрезков линиями. Полезно проверить правильность расчета и построение графика по уравнению потребного напора путем подстановки в него числовых значений величин.
Контрольные вопросы 1) В чем заключается физический смысл уравнения Бернулли для идеальной и реальной жидкости? 2) Что такое "напор"? Поясните составляющие полного напора потока, их определение расчетным путем. 3) Что характеризуют напорная и пьезометрическая линии? Какой вид они имеют при установившемся движении реальной жидкости в трубопроводе: цилиндрическом, расширяющемся, сужающемся? 4) Поясните общую схему применения уравнения Бернулли в практических расчетах. 5) Какие виды гидравлических сопротивлений необходимо учитывать при расчете простого короткого трубопровода? 6) Запишите основные расчетные формулы для потерь напора по длине и в местных сопротивлениях. Поясните влияние величин на потери напора. 7) Поясните определение коэффициентов гидравлического трения и местных сопротивлений.
1.3 Задание по теме«Расчет сопла Лаваля» Сверхзвуковое сопло Лаваля представляет собой насадок, состоящий из короткой сужающейся и длинной расширяющейся частей. По исходным данным: расходу воздуха, параметрам потока при входе в сопло, давлению внешней среды, величине угла раскрытия сопла, следует определить размеры конической сверхзвуковой части круглого поперечного сечения. Расчет может быть выполнен по известным аналитическим зависимостям для определения безразмерных параметров газового потока τ = T/Tо, π = p/pо, ε = ρ/ρо (здесь – Т, р, ρ соответственно температура, давление и плотность газового потока; Tо, pо, ρо - параметры торможения) или с использованием таблиц газодинамических функций [8, 9, 10]. Указанные отношения можно найти в зависимости от числа Маха (М) или от коэффициента скорости l.
Рекомендации по решению: 1) По условию задания трение и теплообмен не учитываются, поэтому параметры торможения в сечениях 1 и 2 равны, т.е. Т01 = Т02; р01 = р02. 2) Температура торможения Т01 и Т02 определяется из уравнения энергии по известным Т1 и u1 (где u1 – скорость в сечении 1); 3) Давление торможения р01 определяется с использованием газодинамических функций р01 = р1/p(М1); 4) Критическая скорость звука определяется по коэффициенту скорости акр = u1/l(М1); 5) Площадь входного сечения w1, и диаметр d1 определяются из уравнения расхода G = ruw по параметрам потока на входе в сопло; 6) Приведенный расход q определяется по известной аналитической зависимости или по таблице q (l); 7) Размеры сопла в наименьшем (критическом) сечении определяются с учетом q = wкр/w1; 8) По функции p(l2) = р2/р02 определяется коэффициент скорости l2 и скорость потока на выходе u2; 9) Площадь выходного сечения сопла w2 = wкр/q(l2); 10) Длина сверхзвуковой части сопла l определяется с учетом wкр, w2 и угла раскрытия сопла 2q.
Содержание пояснительной записки по РГР №3 должно включать: условие задания, исходные данные и расчетную схему; принцип работы сопла Лаваля и основные теоретические положения; определение параметров потока и размеров сопла, анализ полученных результатов. Продольный профиль сопла представить в масштабе на миллиметровке.
Контрольные вопросы 1) Каковы назначение и устройство геометрического сопла Лаваля? 2) Поясните закономерности движения газового потока в сопле Лаваля. 3) Как влияет угол раскрытия сопла на характер движения газа? Укажите рекомендуемые значения этого угла. 4) Параметры потока, соответствующие минимальному сечению сопла, называются …. 5) В чем заключается расчет сопла Лаваля? 6) Какие уравнения газовой динамики используются для расчета течения газового потока в сопле? 7) Что понимают под газодинамическим функциями? Поясните применение графиков и таблиц газодинамических функций. 8) Поясните исходные данные и последовательность расчета сопла Лаваля. 9) Каково соотношение параметров газового потока (скорости, температуры, давления, плотности ) на выходе и входе сопла?
БиблиографиЧЕСКИЙ СПИСОК по гидродинамике
1. Штеренлихт Д.В. Гидравлика. - М.: Энергоатомиздат. 2004. - 624 с. 2. Чугаев Р.Р. Гидравлика. - Л.: Энергоиздат, 1982. 3.Вакина В.В., Денисенко И.Д., Столяров А.Л. Машиностроительная гидравлика (примеры расчетов). - Киев: Вища школа, 1987. -208 с 4. Большаков В.А., Константинов Ю.М., Попов В.Н. и др. Сборник задач по гидравлике. - Киев: Вища шк., 1979. -360 с. 5.Киселев П.Г. Справочник по гидравлическим расчетам. - М.: Энергия,1974. ПО ГАЗОДИНАМИКЕ
6. Самойлович Г.С. Гидрогазодинамика. - М.: Машиностроение, 1990. 7. Дейч М.Е., Зарянкин А.Е. Гидрогазодинамика. – М.: Энергоиздат, 1984. 8. Сергель О.С. Прикладная гидрогазодинамика. – М.: Машиностроение, 1981. 9. Самойлович Г.С. Нитусов В.В. Сборник задач по гидро-аэромеханике. – М.: Машиностроение, 1990. 10. Зарянкин А.Е., Касилов В.Ф. Сборник задач по гидрогазодинамике. – М.: МЭИ,1995

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , (1.8)
, (1.8) - средние скорости в сечениях;
- средние скорости в сечениях; - коэффициенты Кориолиса; учитывают неравномерность распределения скоростей по живому сечению;
- коэффициенты Кориолиса; учитывают неравномерность распределения скоростей по живому сечению;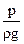 +
+  = H выражает полную удельную энергию жидкости (полный напор).
= H выражает полную удельную энергию жидкости (полный напор). /2g). Полный напор в остальных сечениях Нi = H1-h1-i, где h1-i – суммарные потери напора на участке от сечения 1-1 до i-cечения. Пьезометрический напор в сечениях Hпi=Hi-Hск.i (Hск.i – скоростной напор в соответствующих сечениях).
/2g). Полный напор в остальных сечениях Нi = H1-h1-i, где h1-i – суммарные потери напора на участке от сечения 1-1 до i-cечения. Пьезометрический напор в сечениях Hпi=Hi-Hск.i (Hск.i – скоростной напор в соответствующих сечениях).