
|
|
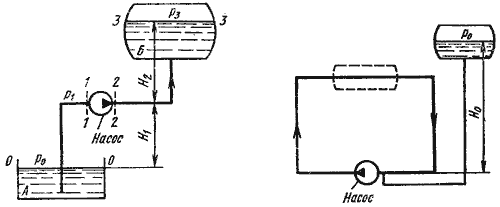
Трубопроводы с насосной подачей жидкостейКак уже отмечалось выше, перепад уровней энергии, за счет которого жидкость течет по трубопроводу, может создаваться работой насоса, что широко применяется в машиностроении. Рассмотрим совместную работу трубопровода с насосом и принцип расчета трубопровода с насосной подачей жидкости. Трубопровод с насосной подачей жидкости может быть разомкнутым, т.е. по которому жидкость перекачивается из одной емкости в другую (рис. 6.8, а), или замкнутым (кольцевым), в котором циркулирует одно и то же количество жидкости (рис. 6.8, б).
Рис. 6.8. Трубопроводы с насосной подачей Рассмотрим трубопровод, по которому перекачивают жидкость из нижнего резервуара с давлением P 0 в другой резервуар с давлением P3 (рис. 6.8, а). Высота расположения оси насоса H1 называется геометрической высотой всасывания, а трубопровод, по которому жидкость поступает к насосу, всасывающим трубопроводом или линией всасывания. Высота расположения конечного сечения трубопровода H2 называется геометрической высотой нагнетания, а трубопровод, по которому жидкость движется от насоса, напорным или линией нагнетания. Составим уравнением Бернулли для потока рабочей жидкости во всасывающем трубопроводе, т.е. для сечений 0-0 и 1-1 (принимая α = 1):
Это уравнение является основным для расчета всасывающих трубопроводов. Теперь рассмотрим напорный трубопровод, для которого запишем уравнение Бернулли, т.е. для сечений 2-2 и 3-3:
Левая часть этого уравнения представляет собой энергию жидкости на выходе из насоса. А на входе насоса энергию жидкости можно будет аналогично выразить из уравнения:
Таким образом, можно подсчитать приращение энергии жидкости, проходящей через насос. Эта энергия сообщается жидкости насосом и поэтому обозначается обычно Hнас. Для нахождения напора Hнас вычислим уравнение :
где Δz - полная геометрическая высота подъема жидкости, Δz = H 1 + H2; Если к действительной разности уровней Δz добавить разность пьезометрических высот ( P3 - Р0 ) ( ρg ), то можно рассматривать увеличенную разность уровней
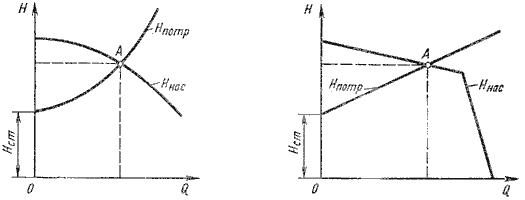
и формулу можно переписать так: Hнас = Hст + KQm Из этой формулы делаем вывод, что Hнас = Hпотр Отсюда вытекает следующее правило устойчивой работы насоса: при установившемся течении жидкости в трубопроводе насос развивает напор, равный потребному. На этом равенстве основывается метод расчета трубопроводов с насосной подачей, который заключается в совместном построении в одном и том же масштабе и на одном графике двух кривых: напора Hпотр = f1(Q) и характеристики насоса Hнас = f2(Q) и в нахождении их точки пересечения (рис. 6.9).
Рис. 6.9. Графическое нахождение рабочей точки Характеристикой насоса называется зависимость напора, создаваемого насосом, от его подачи (расхода жидкости) при постоянной частоте вращения вала насоса. На рис. 6.9 дано два варианта графика: а - для турбулентного режима; б - для ламинарного режима. Точка пересечения кривой потребного напора с характеристикой насоса называется рабочей точкой. Чтобы получить другую рабочую точку, необходимо изменить открытие регулировочного крана (изменить характеристику трубопровода) или изменить частоту вращения вала насоса. Гидравлический удар Гидравлическим ударом называется резкое повышение давления, возникающее в напорном трубопроводе при внезапном торможении потока рабочей жидкости. Этот процесс является очень быстротечным и характеризуется чередованием резких повышений и понижений давления, которое связано с упругими деформациями жидкости и стенок трубопровода. Гидравлический удар чаще всего возникает при резком открытии или закрытии крана или другого устройства, управляемого потоком. Пусть в конце трубы, по которой движется жидкость со скоростью υ0, произведено мгновенное закрытие крана (рис. 6.10, а).
Рис. 6.10. Стадии гидравлического удара При этом скорость частиц, натолкнувшихся на кран, будет погашена, а их кинетическая энергия перейдет в работу деформации стенок трубы и жидкости. При этом стенки трубы растягиваются, а жидкость сжимается в соответствии с увеличением давления на величину ΔPуд, которое называется ударным. Область (сечение n - n), в которой происходит увеличение давления, называется ударной волной. Ударная волна распространяется вправо со скоростью c, называемой скоростью ударной волны. Когда ударная волна переместится до резервуара, жидкость окажется остановленной и сжатой во всей трубе, а стенки трубы - растянутыми. Ударное повышение давления распространится на всю длину трубы (рис. 6.10, б). Далее под действием перепада давления ΔPуд частицы жидкости устремятся из трубы в резервуар, причем это течение начнется с сечения, непосредственно прилегающего к резервуару. Теперь сечение n-n перемещается обратно к крану с той же скоростью c, оставляя за собой выровненное давление P0 (рис. 6.10, в). Жидкость и стенки трубы предполагаются упругими, поэтому они возвращаются к прежнему состоянию, соответствующему давлению P0. Работа деформации полностью переходит в кинетическую энергию, и жидкость в трубе приобретает первоначальную скорость υ0, но направленную теперь в противоположную теперь сторону. С этой скоростью весь объем жидкости стремится оторваться от крана, в результате возникает отрицательная ударная волна под давлением P0 - ΔPуд, которая направляется от крана к резервуару со скоростью c, оставляя за собой сжавшиеся стенки трубы и расширившуюся жидкость, что обусловлено снижением давления (рис. 6.10, д). Кинетическая энергия жидкости вновь переходит в работу деформаций, но противоположного знака. Состояние трубы в момент прихода отрицательной ударной волны к резервуару показано на рис. 6.10, е. Так же как и для случая, изображенного на рис. 6.10, б, оно не является равновесным. На рис. 6.10, ж, показан процесс выравнивания давления в трубе и резервуаре, сопровождающийся возникновением движения жидкости со скоростью υ0. Очевидно, что как только отраженная от резервуара ударная волна под давлением ΔP уд достигнет крана, возникнет ситуация, уже имевшая место в момент закрытия крана. Весь цикл гидравлического удара повторится. Протекание гидравлического удара во времени иллюстрируется диаграммой, представленной на рис. 6.11, а и б. Штриховыми линиями показано теоретическое изменение давления у крана в точке А, а сплошной действительный вид картины изменения давления по времени (рис. 6.11, а). При этом затухание колебаний давления происходит за счет потерь энергии жидкости на преодоление сил трения и ухода энергии в резервуар. Если давление P0 невелико (P0 < ΔP уд), то картина изменения амплитуды давления получается несколько иная, примерно такая, как показано на рис. 6.11, б.
Рис. 6.11. Изменение давления по времени у крана Повышение давления при гидравлическом ударе можно определить по формуле ΔPуд = ρυ0c Данное выражение носит название формулы Жуковского. В нем скорость распространения ударной волны c определится по формуле:
где r - радиус трубопровода; Если предположить, что труба имеет абсолютно жесткие стенки, т.е. E =
Для воды эта скорость равна 1435 м/с, для бензина 1116 м/с, для масла 1200 - 1400 м/с. 5.1 Преобразование энергии в потоке газа
В технике много машин и двигателей, в которых происходят процессы течения газа с трансформацией энергии потока. Течение газа может происходить в цилиндрических трубах, через отверстия или в специально спроектированных каналах. Каналы, в которых происходит увеличение кинетической энергии и снижение потенциальной энергии потока, называются соплами. В сопловых каналах давление газа или пара снижается, а скорость возрастает. Каналы, в которых кинетическая энергия газа уменьшается, а потенциальная возрастает, называются диффузорами. В диффузорах давление увеличивается, а скорость потока уменьшается. Уравнение первого закона термодинамики для потока (2.5), при отсутствии технической работы и нулевом изменении потенциальной энергии в поле гравитационных сил, приобретает следующий вид:
Так как
где Термин “работа” здесь несколько условен, точнее - произведение объёма на приращение давления есть изменение потенциальной энергии. Предполагается, что эта потенциальная энергия при течении газа по соплу, в соответствии с выражением (5.3), превратится в кинетическую, которая затем на лопатках турбины преобразуется в работу перемещения ротора турбины. Процесс адиабатного расширения газа в потоке изображается на диаграмме p - v (рисунок 5.1) линией 1-2. Площадь а-1-2-в по смыслу выражения
представляет собой располагаемую работу процесса. При известных начальных и конечных параметрах состояния располагаемая работа определяется по следующей формуле При сравнении формул (5.5) и (4.34) видно, что располагаемая работа в к раз больше работы изменения объёма:
5.2 О форме сопел и диффузоров.
В формулировках сопел и диффузоров не оговаривается возможная геометрия этих каналов. Это не случайно, так как их продольный профиль зависит от условий течения газа, о чём пойдёт речь ниже. Одним из уравнений, определяющих физико-математическую модель процесса течения газа, является уравнение неразрывности (сплошности): Mv=wA, (5.7) где М - массовый секундный расход газа, n - удельный объем газа, w - скорость потока, А - площадь поперечного сечения канала Смысл уравнения сплошности заключается в том, что массовое количество газа, проходящего в единицу времени одинаково для любого поперечного сечения канала; при переходе от одного сечения канала к другому масса газа не может увеличиться или уменьшиться. В дифференциальном виде при М = Const (массовый расход газа через любое поперечное сечение канала одинаков) уравнение (5.7) выглядит так: d(Mv)=d(wA) и Mdv=wdA+Adw (5.8) После деления (5.8) на (5.7) получается Из дифференциального уравнения адиабаты а из уравнения располагаемой работы (5.3) получается После подстановки из уравнений (5.10) и (5.11) уравнение (5.8) имеет вид Из школьного курса физики известно, что скорость звука определяется выражением C учётом этого формула (5.12) записывается так:
Приращение dA в формуле (5.14) может быть как положительным, так и отрицательным. Это зависит от знака приращения dp и величины, заключенной в скобках. Знак “минус” перед dA означает, что площадь поперечного сечения должна уменьшаться, а положительному приращению dA должно соответствовать расширение канала. В соответствии с формулировками, для сопла dp<0, а для диффузора dp>0. Когда скорость потока меньше скорости звука, величина, заключенная в скобках, всегда положительна, потому что скорость, давление и показатель адиабаты не могут быть отрицательными; если же поток движется со сверхзвуковой скоростью, то она отрицательна. Таблица 5.1
Из таблицы 5.1следует: - когда скорость газа на входе в канал меньше местной (то есть в данном сечении канала) скорости звука, сопло должно быть суживающимся, а диффузор - расширяющимся; - если скорость потока во входном сечении канала превышает местную скорость звука, то сопло должно быть расширяющимся, а диффузор суживающимся.
5.3 Истечение газа из суживающегося сопла
При изучении этого процесса предполагается, что истечение происходит при постоянных параметрах газа на входе в сопло и на выходе из него. Пусть давление cреды, откуда происходит истечение, равно
Сложность при использовании формулы (5.15) заключается в том, что энтальпия газа на выходе из сопла, как правило, неизвестна, и её определение требует дополнительных расчётов. Более удобной представляется формула, в которой были бы задействованы начальные параметры и перепад давлений до и после сопла. Для получения такой формулы используются выражения (5.3-5.5), откуда
и, при условии
Дальнейшие преобразования будут относиться к выражению, заключенному в скобки под корнем:
Если отношение давлений обозначить
Для определения массового расхода газа используется уравнение сплошности применительно к выходному сечению площадью
Для удаления из формулы удельного объёма в выходном сечении производятся следующие преобразования:
После подстановки полученного фрагмента в формулу (5.18), получается:
На основании формул (5.17) и (5.20) на рисунке 5.3 построены графические зависимости скорости истечения и массового расхода газа в суживающемся сопловом канале.
По мере уменьшения b скорость потока в выходном сечении возрастает, и при b = 0, что соответствует истечению в вакуумированное пространство, она достигает максимума:
Проведенные эксперименты по изучению процесса истечения газа показали, что формулы (5.17) и (5.20) справедливы в диапазоне изменения b от единицы до некоторого значения, соответствующего максимальному расходу газа и точке перегиба кривой Для выяснения появившегося несоответствия между теорией и практикой следует вначале определить, от чего зависит и чему равно значение
Последнее выражение можно представить в таком виде
Из формулы (5.23) следует, что критическое отношение давлений зависит только от показателя адиабаты и, с учётом ранее принятых числовых значений показателей адиабаты, составляет для одноатомных газов - 0,485, для двухатомных - 0,527 и для многоатомных - 0,545. Дальнейший анализ сводится к более подробному изучению факторов, влияющих на выходную скорость газа. Из исходной формулы (5.16) находится зависимость скорости потока от критических параметров газа в выходном сечении сопла:
После замены
Если в выражение (5.25) подставить значение критического отношения давлений из формулы (5.23), то, после сокращений, оно предстанет в таком виде:
где
В соответствии с формулой (5.26) критическая скорость потока численно равна скорости звука в выходном сечении сопла. Этот вывод позволяет объяснить причину несоответствия между теорией и практикой, объясняя то, что происходит в канале при различных режимах течения газа. Пока отношение давлений больше критического Уменьшение давления в приёмной среде при постоянном начальном давлении ведёт к увеличению градиента давления и выходной скорости потока. Это продолжается до тех пор, пока в устье сопла не установится критический режим, когда скорость потока оказывается равной местной скорости звука. Дальнейшее понижение давления в приёмной среде (противодавления) не приводит к перераспределению давлений по длине сопла и увеличению градиента давления, так как волны давления перемещаются именно со скоростью звука. Можно сколь угодно понижать давление Изменение скорости потока, местной скорости звука и давления по длине соплового канала в различных режимах течения газа показано на рисунке 5.4 . В докритической области формулы (5.17) и (5.20) для определения скорости истечения и массового расхода используются без всяких оговорок. В критическом режиме эти формулы также справедливы при условии, что в них будет присутствовать значение Для определения скорости в закритическом режиме в формулу (5.17) следует подставлять значение
где удельный объём
5.4 Сопло Лаваля
Для получения сверхзвуковых скоростей при истечении газа или пара применяются комбинированные сопла, состоящие из суживающейся части и расширяющегося патрубка.
О форме соплового канала в сверхзвуковой области уже доказывалось ранее в п.5.2. При установившейся критической скорости истечения на выходе из суживающегося канала дальнейшее увеличение скорости возможно только за счёт организованного, направленного расширения газа, в результате чего объём газа при постоянном массовом расходе газа увеличивается. Для этого и служит расширяющийся насадок. Чтобы в процессе расширения не происходил отрыв потока от стенок, и во избежание нежелательного вихреобразования, угол конусности в расширяющейся части сопла Лаваля обычно принимается равным 8-12°. Правильным подбором длины расширяющегося насадка можно добиться полного преобразования потенциальной энергии газа в кинетическую. Изменение скорости потока w, местной скорости звука а и давления р по длине сопла Лаваля представлено на рисунке 5.5 . Так как в сопловом канале Лаваля происходит расширение газа при полном использовании перепада давления, скорость потока в выходном сечении определяется по формуле (5.17) при действительном значении b . Массовый расход газа здесь определяется пропускной способностью минимального сечения, в котором установились критические условия, поэтому в формулу массового расхода (5.20) следует подставлять критическое отношение давлений Так как массовый расход газа одинаков и в минимальном, и в выходном сечениях, можно записать откуда следует Длина расширяющейся части круглого сопла Лаваля определяется из соотношения где ОА=(D-d)/2. , D - диаметр выходного сечения сопла, d - диаметр минимального сечения сопла. Благодаря разработке теории комбинированных сопел, когда стало возможным эффективно использовать пар высокого давления, мощный толчок получило судовое турбостроение, и в конце 19 - начале 20 века стали эксплуатироваться турбинные установки мощностью в десятки и сотни тысяч киловатт.
5.5 Нерасчётные режимы истечения газа из сопел Изменение давления в среде, откуда происходит истечение, так же как и изменение противодавления при течении газа в суживающемся сопле, отражается на скорости истечения в соответствии с закономерностями, выясненными выше в п.5.3. При нерасчётных режимах никаких сложностей и новых особенностей здесь не возникает. В канале Лаваля, предназначенном для работы в условиях закритического течения газа, изменение противодавления в сторону увеличения приводит к тому, что в некотором сечении х – х расширяющейся части сопла давление газа рх становится меньше противодавления р2 (точка 2 на рисунке 5.6), в связи с чем следует резкое повышение давления газа (процесс 2-3). Такой процесс повышения давления называется скачком давления. После скачка давления скорость течения газа становится сразу дозвуковой. Участок сопла за сечением х – х начинает работать как диффузор, в котором давление возрастает по линии 3-4.
При повышении противодавления больше критического давление газа будет изменяться по линии 1-5-6-7, и в этом случае выходная скорость газа будет меньше скорости звука. Пояснить случившееся можно, проанализировав следующую ситуацию. Если на пути потока, движущегося по трубе, внезапно установить препятствие в виде диафрагмы, то у диафрагмы возникнет волна давления, которая будет двигаться навстречу потоку и по ходу его со скоростью звука. Встречное движение волны будет устанавливать повышенное давление до диафрагмы со скоростью, равной разности скоростей звука и потока. За диафрагмой давление останется равным противодавлению. Сверхзвуковой поток в аналогичных условиях ведёт себя иначе. Волна давления, возникшая у диафрагмы, не может проникнуть навстречу потоку, потому что он движется со сверхзвуковой скоростью. Эта волна может распространяться только в направлении движения потока, поэтому давление за диафрагмой возрастает. Это новое давление может оказаться больше противодавления приёмной среды. Если противодавление за соплом Лаваля станет больше расчётного, то на срезе сопла возникает волна давления, которая со скоростью звука внедряется в сверхзвуковой поток. В результате взаимодействия скоростей образовавшаяся волна давления принимает коническую форму и переходит в так называемый косой скачок давления z-z¹-z . Давление за наружной поверхностью конуса равно противодавлению окружающей среды р2, а внутри конуса давление меньше. Протяженность скачка давления очень мала и оценивается длиной свободного пробега молекул. Кроме неприятностей в виде скачка давления, увеличение противодавления может привести к отрыву струи от стенок сопла. Волна давления, возникшая у выходной кромки сопла, может распространиться внутрь сопла по пограничному слою, где скорость движения газа может быть меньше скорости звука. Следует помнить, что по теории пограничного слоя скорость газа или жидкости, соприкасающейся с поверхностью канала равна нулю. Здесь, в расширяющейся части сопла может возникнуть ещё один скачок давления y-y¹-y.
5.6 Термодинамические процессы в турбине и компрессоре
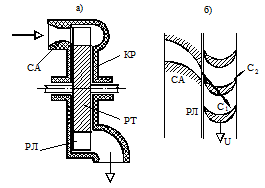
Принцип действия турбины показан на рисунке 5.7. В корпусе КР на валу находится диск РТ с лопатками РЛ, имеющими определённый профиль. Перед лопатками установлены сопла СА, к которым подводится газ или пар с высоким давлением. При расширении рабочего тела происходит увеличение скорости потока, и на выходе из сопла эта скорость С1 составляет сотни или даже тысячи метров в секунду. Попав в межлопаточное пространство, поток изменяет направление движения (в идеальном случае на 180˚), в результате чего создаётся сила, образующая момент вращения с плечом, равным радиусу окружности. Скорость газа при этом уменьшается до С2. Кинетическая энергия газового потока трансформируется в энергию движения ротора (диска с лопатками). Работа процесса, совершаемая газом или паром в условиях открытой термодинамической системы, которой является турбина, называется технической или располагаемой работой (о ней упоминалось ранее при рассмотрении первого закона термодинамики). Для идеальной турбины, в которой отсутствуют тепловые потери и потери на трение, уравнение первого закона термодинамики записывается в таком виде: но при отсутствии тепловых потерь
а работа газа в процессе адиабатного процесса расширения1-2 равна:
Следовательно, удельная работа, совершаемая рабочим телом в турбине, равна разности удельных энтальпий перед входом в турбину и на выходе из неё. Адиабатный процесс, происходящий в турбине, показан в диаграммах p – v и T – s на рисунке 5.8. Заштрихованная площадь 12аб определяет работу при расширении и перемещении газа. При расширении рабочего тела в турбине давление его снижается, и работа, в соответствии с выражением (5.32), получается положительной. Из уравнения политропы (4.3) следует:
что означает – удельная работа открытой системы (располагаемая работа) в п раз больше работы изменения объёма закрытой системы. Адиабатный процесс является частным случаем политропных процессов при п = к, поэтому, на основании формулы 4.34, адиабатному расширению газа в турбине соответствует удельная работа, определяемая по формуле
 (5.33) (5.33)
Антиподы турбин – лопаточные компрессоры применяются в газотурбинных установках, в турбонагнетателях поршневых двигателей, а также в других машинах, где требуется перемещение и сжатие упругих веществ (газов или паров). Упрощенная модель открытой термодинамической системы, имитирующей компрессор, показана на рисунке 5.9,а. Пусть на входе в компрессор параметры газа равны p1,v1,T1,h1, а на выходе – p2,v2,T2,h2. Для такой системы справедливо уравнение первого закона термодинамики 5.30, а при условии адиабатности процесса – уравнение 5.31. Техническая работа, затраченная на сжатие и перемещение газа в идеальном лопаточном компрессоре определяется по формуле 5.32, которая может быть представлена в таком виде:
где β = р2/р1 – перепад давлений, который создаёт компрессор. Работа, подсчитанная по формуле (5.34), отрицательна, так как компрессор – машина, потребляющая энергию. Процесс сжатия, происходящий в компрессоре, на диаграмме p – v изображается линией 1-2, а заштрихованная площадь на рисунке 5.9 представляет собой теоретическую работу компрессора.
СОДЕРЖАНИЕ стр. Предисловие..............................................................…...............................................3 1. Содержание дисциплины ...............................…....................................................3 2. Литература…………………………..……………………………………..………8 3. Задание на контрольную работу...…......................................................................9 4. Методические указания по практическим занятиям…………………………...13 Приложение………………………………………………………………………....16
ЛИТЕРАТУРА Основная: 1. Лабейш В.Г. Гидравлические расчеты энергооборудования: Л.: СЗПИ, 1991. 92 с. 2. Лабейш В.Г. Газодинамика: Л.: СЗПИ, 1990. 84 с.
Дополнительная: 3. Лабейш В.Г. Гидромеханика и газодинамика: Л.: СЗПИ, 1973. 186 с. 4. Дейч М.Е., Зарянкин А.Е. Гидрогазодинамика: М.: Энергоатомиздат, 1984. 384 с. 5. Кириллов П.Л., Юрьев Ю.С., Бобков В.П. Справочник по теплогидравлическим расчетам: М.: Энергоатомиздат, 1984. 296 с. 6. Самойлович Г.С., Нитусов В.В. Сборник задач по гидроаэромеханике: М.: Машиностроение, 1986. 152 с.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

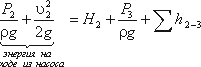
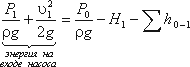

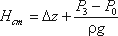


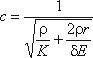
 , то скорость ударной волны определится из выражения
, то скорость ударной волны определится из выражения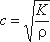
 (5.1)
(5.1) В соплах и диффузорах скорость движения газа достаточно велика, а размеры этих каналов, как правило, небольшие, поэтому за то время, когда газ течёт по каналу, он не успевает передавать теплоту в окружающую среду. В связи с этим процессы течения в дальнейшем будут рассматриваться как адиабатные. Для них
В соплах и диффузорах скорость движения газа достаточно велика, а размеры этих каналов, как правило, небольшие, поэтому за то время, когда газ течёт по каналу, он не успевает передавать теплоту в окружающую среду. В связи с этим процессы течения в дальнейшем будут рассматриваться как адиабатные. Для них (5.2)
(5.2) но
но  , поэтому
, поэтому
 , (5.3)
, (5.3) - элементарная располагаемая работа.
- элементарная располагаемая работа. (5.4)
(5.4) (5.5)
(5.5) (5.6)
(5.6) (5.9)
(5.9) следует
следует  , ( 5.10)
, ( 5.10) (5.11)
(5.11) (5.12)
(5.12) (5.13)
(5.13) (5.14)
(5.14)





 , а давление той cреды, куда вытекает газ (так называемое противодавление), равно
, а давление той cреды, куда вытекает газ (так называемое противодавление), равно  . Пусть начальные параметры газа (на входе в сопло) известны и равны
. Пусть начальные параметры газа (на входе в сопло) известны и равны  .
. Скорость газа на выходе из сопла можно определить, используя формулу (5.2), откуда при условии, что выходная скорость значительно больше скорости газа на входе (
Скорость газа на выходе из сопла можно определить, используя формулу (5.2), откуда при условии, что выходная скорость значительно больше скорости газа на входе (  ), получается
), получается
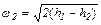 (5.15)
(5.15) ,
, (5.16)
(5.16)
 , то, после подстановки предыдущего выражения в формулу (5.16), получается
, то, после подстановки предыдущего выражения в формулу (5.16), получается (5.17)
(5.17) :
: (5.18)
(5.18) (5.19)
(5.19) (5.20)
(5.20) При b = 1, когда давление до и после сопла одинаково, движение потока отсутствует, скорость и массовый расход газа равны нулю.
При b = 1, когда давление до и после сопла одинаково, движение потока отсутствует, скорость и массовый расход газа равны нулю. (5.21)
(5.21) Определённое недоумение вызывают результаты анализа формулы (5.20) - с уменьшением b массовый расход газа вначале увеличивается, как это показано на рисунке 5.3 , но, достигнув максимума, начинает уменьшаться и при b = 0 становится равным нулю. Парадокс - газ вытекает с огромной скоростью, но не расходуется, то есть теряет материальную сущность.
Определённое недоумение вызывают результаты анализа формулы (5.20) - с уменьшением b массовый расход газа вначале увеличивается, как это показано на рисунке 5.3 , но, достигнув максимума, начинает уменьшаться и при b = 0 становится равным нулю. Парадокс - газ вытекает с огромной скоростью, но не расходуется, то есть теряет материальную сущность. . При дальнейшем уменьшении b скорость истечения и массовый расход газа остаются постоянными, как бы ни изменялось давление приёмной среды.
. При дальнейшем уменьшении b скорость истечения и массовый расход газа остаются постоянными, как бы ни изменялось давление приёмной среды.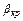 . Для этого берётся первая производная от функции, заключенной в скобках уравнения (5.20), и приравнивается нулю:
. Для этого берётся первая производная от функции, заключенной в скобках уравнения (5.20), и приравнивается нулю: (5.22)
(5.22) (5.23)
(5.23) (5.24)
(5.24) получается
получается (5.25)
(5.25) , (5.26)
, (5.26) - местная, то есть в выходном сечении, скорость звука
- местная, то есть в выходном сечении, скорость звука
 , в сопловом канале устанавливается режим течения, соответствующий теоретическому распределению давления по длине канала от
, в сопловом канале устанавливается режим течения, соответствующий теоретическому распределению давления по длине канала от  , где
, где  - давление газа в выходном сечении сопла.. Наличие градиента давления вдоль соплового канала приводит к преобразованию потенциальной энергии потока в кинетическую по известному соотношению
- давление газа в выходном сечении сопла.. Наличие градиента давления вдоль соплового канала приводит к преобразованию потенциальной энергии потока в кинетическую по известному соотношению  , в результате чего поток на выходе приобретает интегральную скорость
, в результате чего поток на выходе приобретает интегральную скорость  .
. . Такие режимы течения называют закритическими.
. Такие режимы течения называют закритическими. , определяемое по формуле (5.23).
, определяемое по формуле (5.23). , независимо от действительного отношения давлений
, независимо от действительного отношения давлений  . Массовый расход газа в закритическом режиме определяется по формуле (5.20) при тех же условия её использования, либо по уравнению сплошности
. Массовый расход газа в закритическом режиме определяется по формуле (5.20) при тех же условия её использования, либо по уравнению сплошности , (5.27)
, (5.27) определяется по соотношению между параметрами в адиабатном процессе расширения газа:
определяется по соотношению между параметрами в адиабатном процессе расширения газа: .
.

 .
. , (5.28)
, (5.28)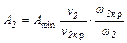 (5.29)
(5.29)

 Турбина является одним из элементов газотурбинного двигателя, работающего по круговому процессу. Кроме того, в турбинах используется энергия отработанных газов поршневых ДВС для привода нагнетателей, позволяющих повысить мощность установок. Турбины также применяются в холодильных установках и системах кондиционирования воздуха. В зависимости от применяемого рабочего тела турбины подразделяются на паровые и газовые.
Турбина является одним из элементов газотурбинного двигателя, работающего по круговому процессу. Кроме того, в турбинах используется энергия отработанных газов поршневых ДВС для привода нагнетателей, позволяющих повысить мощность установок. Турбины также применяются в холодильных установках и системах кондиционирования воздуха. В зависимости от применяемого рабочего тела турбины подразделяются на паровые и газовые.
 , (5.30)
, (5.30) , поэтому
, поэтому , (5.31)
, (5.31) (5.32)
(5.32) ,
,

 , (5.34)
, (5.34)