
|
|
I. РАСПРОСТРАНЕНИЕ ВОЛН В УПРУГОЙ СРЕДЕОПРЕДЕЛЕНИЕ СКОРОСТИ РАСПРОСТРАНЕНИЯ КОЛЕБАНИЙ В ВОЗДУХЕ И ТВЁРДЫХ ТЕЛАХ
Методические указания к лабораторной работе
Дисциплина "Физика" для всех специальностей
Киров – 2009 УДК 534.538
Рецензент: кандидат химических наук, доцент кафедры физики ВСГХА В.А. Морозов
Определение скорости распределения колебаний в воздухе и твердых телах: Лабораторная работа / Р.В. Хомяков.– Киров: Изд-во ВятГУ, 2009.– 15с.
Компьютерный набор: К.В. Машковцев
____________________________________________________
610000, г. Киров, ул. Московская, 36.
Цель работы: познакомиться с методами определения скорости звука в воздухе и металлическом стержне.
I. РАСПРОСТРАНЕНИЕ ВОЛН В УПРУГОЙ СРЕДЕ
Если в каком-либо месте упругой (твердой, жидкой или газообразной) среды возбудить колебания её частиц, то вследствие взаимодействия между частицами это колебание будет распространяться в этой среде. Процесс распространения колебаний в пространстве называется волной. Каждая частица становится источником вторичных волн и колебания распространяются в упругой среде с некоторой скорость Частицы среды, в которой распространяется волна, не вовлекаются волной в поступательное движение, они лишь совершают колебания около своих положений равновесия. В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различаю продольные и поперечные волны. В продольной волне частицы среды колеблются вдоль направления распространения волны. В поперечной волне частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Поперечные волны могут возникнуть лишь в следах, обладавших упругим сопротивлением сдвигу. Поэтому в жидкостях и газах возможно возникновение только продольных волн. В твердых телах могут возникнуть как продольные, так и поперечные волны. Распространяясь от источника колебаний, волновой процесс охватывает всё новые и новые части пространства. Поверхность, отделяющая колеблющейся частицы среды от частиц ещё не пришедших в колебание, называется фронтом волны. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновую поверхность можно, провести через любую точку пространства, охваченного волновым процессом. Следовательно, волновых поверхностей существует бесконечное множество, в то время как волновой фронт в каждый момент времени только один. Волновые поверхности остаются неподвижными волновой фронт всё время перемешается. Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сферической. В плоской волне волновые поверхности представляют собой множество параллельных друг другу плоскостей, в сферической волне - множество концентрических сфер. Уравнением волны называется выражение, определяющее смещение колеблющейся частицы как функцию её координат и времени. Для плоской волны распространяющейся вдоль оси x:
Пусть точки, лежащие в плоскости
Найдем вид уравнения колебания точек в плоскости, соответствующей произвольному значению x. Для того чтобы пройти путь от плоскости
где A - амплитуда волны,
Время одного полного колебания называется периодом колебания T.
Расстояние Очевидно, что
где Волна, распространяющаяся в противоположном направлении, описывается уравнением:
Уравнению плоской волны можно придать симметричный вид относительно x и t. Для этого введём величину
Величина k называется волновым числом.
Раскрыв в уравнении (1) скобки и приняв во внимание величину (3), придём к следующему уравнению плоской волны, распространяющейся вдоль оси x:
Уравнение любой волны является решением дифференциального уравнения, называемого волновым. Для плоской волны, распространяющейся вдоль оси x, волновое уравнение имеет вид
Вывод волнового уравнения изложен в пособии /3/.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 © ГОУ ВПО «Вятский государственный университет», 2009
© ГОУ ВПО «Вятский государственный университет», 2009 .
.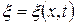 .
.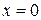 (начало отсчёта), колеблются по закону:
(начало отсчёта), колеблются по закону: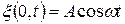 .
. На рисунке 1 показан график функции
На рисунке 1 показан график функции  . Следовательно, колебания частиц, лежащих в плоскости x будут отставать по времени на
. Следовательно, колебания частиц, лежащих в плоскости x будут отставать по времени на  секунд от колебаний частиц в плоскости x = 0, т.е. приобретут вид:
секунд от колебаний частиц в плоскости x = 0, т.е. приобретут вид: . (1)
. (1) - циклическая; частота колебания,
- циклическая; частота колебания,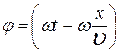 - фаза колебания.
- фаза колебания. .
. , на которое распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны.
, на которое распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны. , (2)
, (2)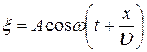 .
. . (3)
. (3) . (4)
. (4) .
.