Отображения множеств. Линейные операторы и их матрицы.
Занятие 3 (Фдз 4).
3.1. Отображения множеств. Образ и прообраз. Однозначное и взаимно однозначное отображения, примеры. Обратное отображение. Композиция отображений.
3.2. Линейный оператор, его свойства, примеры линейных операторов.
3.3. Матричная запись действия линейного оператора в заданном базисе. Матрица линейного оператора и ее преобразование при переходе к новому базису.
3.1. Пусть даны два множества 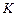 и и 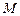 , и задан некоторый закон , и задан некоторый закон  , по которому каждому элементу из множества , по которому каждому элементу из множества 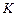 ставится в соответствие один или несколько элементов множества ставится в соответствие один или несколько элементов множества 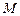 . Тогда говорят, что задано отображение (преобразование) . Тогда говорят, что задано отображение (преобразование)  множества множества 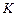 на множество на множество 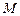 . .
Если отображение  ставит в соответствие каждому элементу множества ставит в соответствие каждому элементу множества 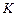 ровно один элемент из множества ровно один элемент из множества 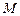 , то отображение , то отображение  называется однозначным отображением. Пусть элементу называется однозначным отображением. Пусть элементу 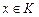 отображение отображение  ставит в соответствие элемент ставит в соответствие элемент 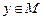 , тогда принято писать , тогда принято писать 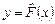 , и элемент , и элемент  называют образом элемента называют образом элемента  , а элемент , а элемент  - прообразом элемента - прообразом элемента  заданного отображения заданного отображения  . Множество всех образов отображения . Множество всех образов отображения  обозначается обозначается  и называется образом множества и называется образом множества 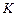 . .
Если 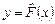 является однозначным отображением множества является однозначным отображением множества 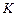 на множество на множество 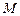 , и каждый образ , и каждый образ 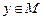 имеет только один прообраз имеет только один прообраз 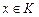 , то такое отображение называется взаимно однозначным. , то такое отображение называется взаимно однозначным.
Если даны два однозначных отображения  и и  , то определено однозначное отображение , то определено однозначное отображение  . Отображение . Отображение 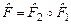 называется композицией отображений называется композицией отображений  и и 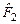 . .
Если  - взаимно однозначное отображение - взаимно однозначное отображение  , то существует обратное отображение , то существует обратное отображение  , действующее по правилу: , действующее по правилу:
 . .
Композиция отображений 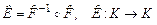 является тождественным отображением: является тождественным отображением: 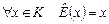 . .
Пример 1. Пусть 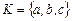 - множество, состоящее из трех элементов - множество, состоящее из трех элементов 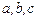 и и  - множество, состоящее из пяти элементов - множество, состоящее из пяти элементов 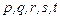 . .
1) Пусть задано отображение 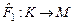 , такое, что , такое, что  . .
Закон 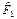 : :
переводит элемент 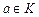 в множество в множество  , где , где 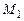 состоит из двух элементов состоит из двух элементов 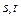 ; ;
переводит элемент 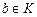 в множество в множество 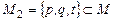 ; ;
переводит элемент 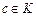 в элемент в элемент 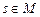 . .
Следовательно,
образом элемента 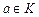 является множество является множество  , ,
образом элемента 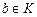 является множество является множество 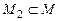 , ,
образом элемента 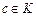 является элемент является элемент  , ,
образом всего множества 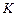 является множество является множество 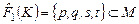 . .
Прообраз элемента 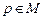 состоит из одного элемента состоит из одного элемента 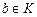 , ,
прообраз элемента 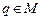 также состоит из одного элемента также состоит из одного элемента 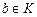 , ,
прообразом элемента 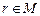 служит пустое множество служит пустое множество 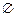 , ,
прообраз элемента 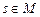 представляет множество представляет множество 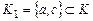 , ,
прообраз элемента  представляет множество представляет множество 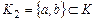 . .
Отображение 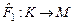 не является однозначным отображением (т.к. образом элемента не является однозначным отображением (т.к. образом элемента 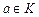 является не один, а два элемента множества является не один, а два элемента множества 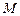 ). ).
2) Пусть задано отображение 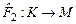 , действующее так: , действующее так:  . .
Здесь 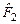 : :
переводит элемент 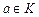 в элемент в элемент 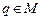 (образом элемента (образом элемента 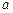 является один элемент является один элемент 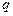 ); переводит элемент ); переводит элемент 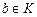 в элемент в элемент  (образом элемента (образом элемента 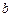 является один элемент является один элемент  ); переводит элемент ); переводит элемент 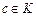 в элемент в элемент 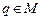 (образом элемента (образом элемента  является один элемент является один элемент 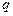 ); );
 . .
Прообразы элементов 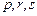 - пустые множества. - пустые множества.
Прообраз элемента 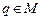 представляет множество из двух элементов представляет множество из двух элементов 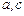 . .
Прообраз элемента  состоит из одного элемента состоит из одного элемента 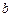 . .
Преобразование 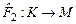 является однозначным отображением, но не является взаимно однозначным (по двум причинам: прообразы элементов является однозначным отображением, но не является взаимно однозначным (по двум причинам: прообразы элементов 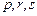 пусты; и прообраз элемента пусты; и прообраз элемента 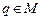 состоит из двух элементов состоит из двух элементов 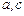 ). ).
Пример 2. Отображение  , где , где
 - множество всех векторов в трехмерном пространстве, - множество всех векторов в трехмерном пространстве, 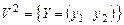 - множество всех векторов на плоскости, - множество всех векторов на плоскости,
 . (1) . (1)
Найти образ вектора  и прообраз вектора и прообраз вектора  . .
Решение. Чтобы найти образ 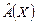 подставим координаты вектора подставим координаты вектора 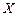 в формулы (1): в формулы (1):
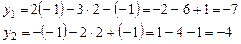  . .
Чтобы найти прообраз вектора  , подставим координаты этого вектора в уравнения (1) и решим полученную систему относительно координат , подставим координаты этого вектора в уравнения (1) и решим полученную систему относительно координат 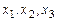 . .
 , , 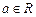 . .
(Вторая система из первой получена так: к 1-му уравнению прибавили 2-е уравнение и затем переставили местами 2-е и полученное 1-е уравнения).
Таким образом, прообразом вектора  служит множество векторов служит множество векторов 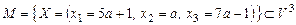 , зависящее от одного параметра , зависящее от одного параметра 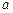 . .
Приведем примеры взаимно однозначных отображений  и обратных им отображений и обратных им отображений 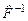 . .
1) Пусть 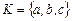 , ,  , , 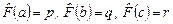 . .  - взаимно однозначное отображение. Обратное отображение - взаимно однозначное отображение. Обратное отображение 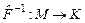 действует так: действует так:
 . .
2) Пусть 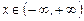 , ,  . Отображение . Отображение 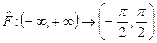 , определенное по правилу , определенное по правилу 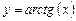 , является взаимно однозначным отображением. Обратным отображением , является взаимно однозначным отображением. Обратным отображением  будет закон: будет закон: 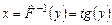 . .
3) Пусть 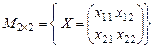 - множество всех квадратных матриц второго порядка. - множество всех квадратных матриц второго порядка.
Отображение  , заданное по правилу , заданное по правилу 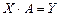 , где , где 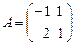 , однозначно определяет по заданной матрице , однозначно определяет по заданной матрице 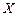 ее образ (матрицу ее образ (матрицу  ). ).
Т.к. определитель матрицы 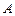 отличен от нуля, то по заданному образу (матрице отличен от нуля, то по заданному образу (матрице  ) находится ее единственный прообраз – матрица ) находится ее единственный прообраз – матрица  . Следовательно, . Следовательно,  - взаимно однозначно отображает множество - взаимно однозначно отображает множество  на множество на множество  . Обратное отображение . Обратное отображение 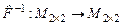 действует так: действует так: 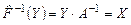 . .
Пример 3. 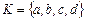 , ,  , , 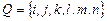 . Даны два однозначных отображения . Даны два однозначных отображения
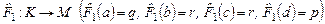 и и  . .
Найти отображение 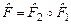 - композицию отображений - композицию отображений  и и 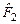 . .
Решение.
Согласно определению композиции отображений имеем:
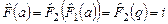 ; ;  ; ; 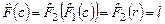 ; ;
 . Следовательно, . Следовательно, 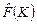 - множество из трех элементов - множество из трех элементов  . .
3.2. Отображение  называется оператором, если называется оператором, если 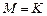 (т.е. (т.е. 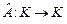 ). ).
Если 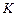 и и 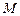 - линейные пространства, и - линейные пространства, и  - отображение, обладающее свойствами: - отображение, обладающее свойствами:
 ; (2) ; (2)
 , (3) , (3)
то такое отображение 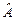 называют линейным отображением. называют линейным отображением.
Оператор 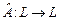 , определенный на линейном пространстве , определенный на линейном пространстве 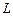 и обладающий свойствами (2), (3), называется линейным оператором. и обладающий свойствами (2), (3), называется линейным оператором.
Свойства (2), (3) можно заменить одним:
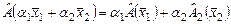 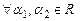 и и 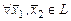 . (4) . (4)
Свойства (2), (3) и обобщающее их свойство (4) называются свойствами линейности.
Из свойства (3) выводится: 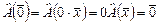 . Следовательно, любой линейный оператор . Следовательно, любой линейный оператор 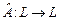 переводит нулевой элемент линейного пространства переводит нулевой элемент линейного пространства 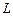 в нулевой элемент. в нулевой элемент.
Пример 4. Доказать линейность отображения  из примера 2. из примера 2.
Решение.
Заменим формулы (1), определяющие заданное отображение матричным равенством
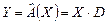 , где , где  . (5) . (5)
Пусть 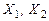 - два произвольных вектора из пространства - два произвольных вектора из пространства 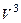 и и 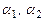 - два произвольных числа. На основании равенства (5), выводим - два произвольных числа. На основании равенства (5), выводим
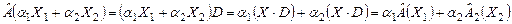 . .
Таким образом, установлено выполнение свойства линейности (4). Это доказывает линейность отображения 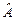 . .
Пример 5. Доказать, что отображение  , , 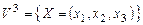 , , 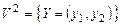 , ,
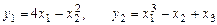 , (6) , (6)
не является линейным отображением.
Решение.
Покажем, что для заданного отображения свойство (3) не выполн.яется. Пусть 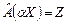 . .
Т.к.  и и 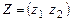 , то согласно закону (6) , то согласно закону (6)
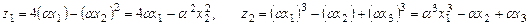 . (7) . (7)
С другой стороны,  , где , где 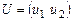 . .
 . (8) . (8)
Из (7), (8) видно, в общем случае  и и 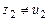 . Следовательно, . Следовательно,  . Значит, . Значит, 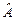 - нелинейное отображение. - нелинейное отображение.
Пример 6. Доказать, что отображение 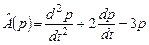 , действующее в пространстве многочленов , действующее в пространстве многочленов  , является линейным оператором , является линейным оператором
Решение.
1. Сначала покажем, что 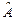 - оператор. - оператор.  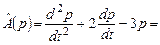  - оператор. - оператор.
2. Теперь докажем линейность 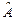 с помощью обобщенного свойства линейности (4). с помощью обобщенного свойства линейности (4).
Пусть 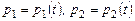 - два произвольных многочлена из пространства - два произвольных многочлена из пространства 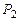 и и 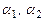 - два произвольных числа. - два произвольных числа.

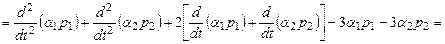

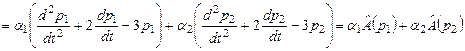 . .
Свойство (4) выполнено и значит, заданный оператор 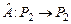 - линейный оператор. - линейный оператор.
Пример 7. Выяснить, является или нет отображение 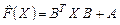 , (где , (где 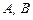 -заданные квадратные матрицы второго порядка), действующее в пространстве матриц -заданные квадратные матрицы второго порядка), действующее в пространстве матриц  , линейным оператором? , линейным оператором?
Решение.
1.  - оператор. - оператор.
2. Пусть 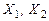 - две произвольные матрицы из пространства - две произвольные матрицы из пространства  . .
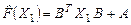 , , 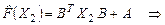
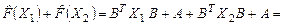 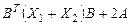 . .
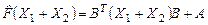 . .
Следовательно, 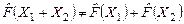 . Не выполнение свойства (2) означает, что заданный оператор . Не выполнение свойства (2) означает, что заданный оператор 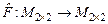 не является линейным. не является линейным.
Пример 8. Доказать, что отображение  множества множества 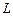 всех матриц всех матриц  , определенное формулой , определенное формулой 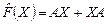 , где , где  , является линейным оператором. , является линейным оператором.
Решение.
1) Пусть  - произвольные матрицы из множества - произвольные матрицы из множества 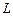 и и
 - произвольные числа. - произвольные числа.
  . .
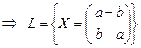 - линейное подпространство в пространстве - линейное подпространство в пространстве 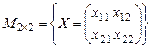 . .
2) Покажем теперь, что  . .
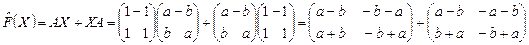 = =
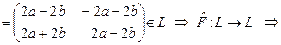  - оператор. - оператор.
3) Осталось доказать линейность оператора  . .
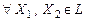 и и 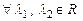

  - линейный оператор. - линейный оператор.
3.3. Пусть: 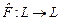 - линейный оператор, действующий в линейном пространстве - линейный оператор, действующий в линейном пространстве 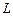 размерности размерности  ; ;  - базис пространства - базис пространства 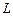 ; ; 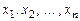 - координаты вектора - координаты вектора 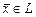 в этом базисе в этом базисе 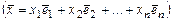 ; ; 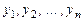 - координаты вектора - координаты вектора 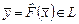 , являющегося образом вектора , являющегося образом вектора 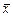 . Тогда действие оператора . Тогда действие оператора  в базисе в базисе 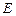 определяется матричным равенством определяется матричным равенством
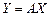 , где , где 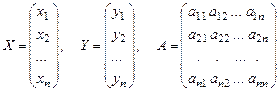 . (9) . (9)
Матрица 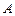 называется матрицей линейного оператора называется матрицей линейного оператора  в базисе в базисе 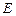 . Эту матрицу находят так: . Эту матрицу находят так:
 - первый столбец матрицы - первый столбец матрицы  ; ;
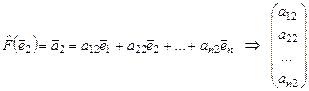 - второй столбец матрицы - второй столбец матрицы  ; и т.д. ; и т.д.
Если наряду с базисом  задан другой (новый) базис задан другой (новый) базис 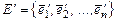 и и  - координаты вектора - координаты вектора 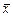 в базисе в базисе 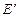 ; ;  - координаты вектора - координаты вектора  в базисе в базисе 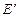 , то действие оператора , то действие оператора  в новом базисе в новом базисе 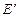 определяется матричным равенством определяется матричным равенством
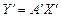 , (10) , (10)
где  . .
Матрица  - матрицей линейного оператора - матрицей линейного оператора  в базисе в базисе 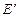 . Она связана с матрицей . Она связана с матрицей 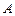 формулой формулой
 , (11) , (11)
где 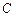 - матрица перехода от базиса - матрица перехода от базиса 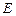 к базису к базису 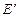 . .
Пример 9. Найти матрицу 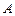 линейного оператора линейного оператора  , действующего в пространстве многочленов , действующего в пространстве многочленов  по правилу по правилу 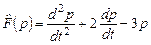 , в стандартном базисе , в стандартном базисе 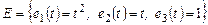 . С помощью найденной матрицы . С помощью найденной матрицы 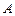 записать действие оператора записать действие оператора  в форме матричного равенства (9). в форме матричного равенства (9).
Решение.
По разложениям образов 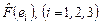 элементов базиса элементов базиса 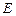 по этому базису найдем соответствующие столбцы искомой матрицы по этому базису найдем соответствующие столбцы искомой матрицы 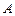 оператора оператора  . .
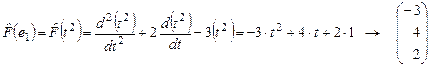 - 1-й столбец матрицы - 1-й столбец матрицы 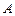 . .
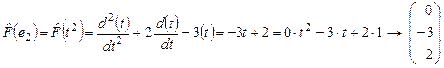 - 2-й столбец матрицы - 2-й столбец матрицы  . .
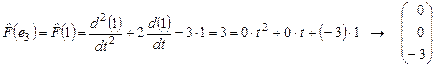 - 3-й столбец матрицы - 3-й столбец матрицы  . .
Следовательно, матрица оператора  в базисе в базисе  имеет вид имеет вид  . .
В нашем случае,  . .
 . .
Формула (9) (закон действия оператора  в заданном базисе в заданном базисе 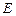 ) перепишется так: ) перепишется так:
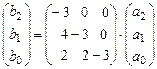 . .
Из этой формулы находим координаты 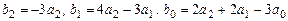 в базисе в базисе 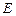 для образа для образа 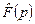 функции функции 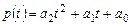 . По координатам . По координатам  восстанавливаем явное выражение для восстанавливаем явное выражение для 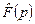 : :
 . .
Этот результат легко проверить непосредственным вычислением 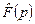 по заданному закону действия линейного оператора по заданному закону действия линейного оператора  на многочлен на многочлен 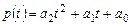 : :
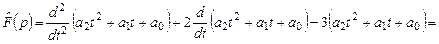
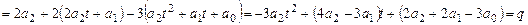 . .
Пример 10. Найти матрицы линейного оператора  из примера 8 в базисах из примера 8 в базисах
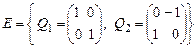 и и  . .
Решение.
1) Найдем матрицу  линейного оператора линейного оператора  в базисе в базисе 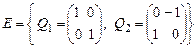 . .
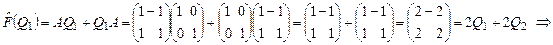  - 1-й столбец матрицы - 1-й столбец матрицы  . .
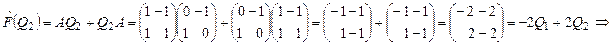  - 2-й столбец матрицы - 2-й столбец матрицы  . .
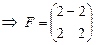 - матрица линейного оператора - матрица линейного оператора  в базисе в базисе 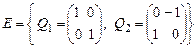 . .
2) Матрицу  линейного оператора линейного оператора  в базисе в базисе  найдем с помощью формулы (11), которая в нашем случае примет вид найдем с помощью формулы (11), которая в нашем случае примет вид  . .
Найдем матрицу 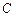 перехода от базиса перехода от базиса 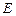 к базису к базису 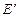 . .
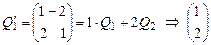 - 1-й столбец - 1-й столбец 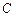 . .
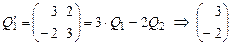 - 2-й столбец - 2-й столбец 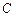 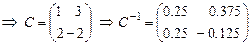 . .
 . .
___________________________________________________________________________
Домашнее задание.
1. Доказать линейность оператора 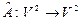 , если в базисе , если в базисе 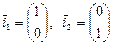 действие этого оператора производится по формулам действие этого оператора производится по формулам 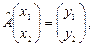 где где 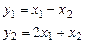 . Найти матрицу этого оператора в базисе . Найти матрицу этого оператора в базисе  и в базисе и в базисе 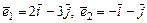 . .
2. Доказать, что отображение 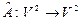 , , 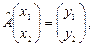 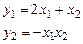 является оператором, но не является линейным оператором. Найти образ вектора является оператором, но не является линейным оператором. Найти образ вектора 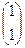 и все прообразы вектора и все прообразы вектора 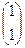 . .
3. Доказать, что отображение 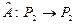 , , 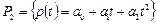 , ,  является линейным оператором и найти матрицу этого оператора в стандартном базисе является линейным оператором и найти матрицу этого оператора в стандартном базисе 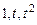 и базисе и базисе 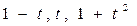 . .
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 и
и 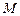 , и задан некоторый закон
, и задан некоторый закон  , по которому каждому элементу из множества
, по которому каждому элементу из множества  множества
множества 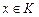 отображение
отображение 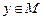 , тогда принято писать
, тогда принято писать 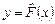 , и элемент
, и элемент  называют образом элемента
называют образом элемента  , а элемент
, а элемент  и называется образом множества
и называется образом множества  и
и  , то определено однозначное отображение
, то определено однозначное отображение  . Отображение
. Отображение 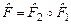 называется композицией отображений
называется композицией отображений  и
и 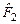 .
. , то существует обратное отображение
, то существует обратное отображение  , действующее по правилу:
, действующее по правилу: .
.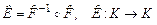 является тождественным отображением:
является тождественным отображением: 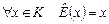 .
.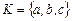 - множество, состоящее из трех элементов
- множество, состоящее из трех элементов 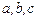 и
и  - множество, состоящее из пяти элементов
- множество, состоящее из пяти элементов 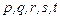 .
. 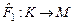 , такое, что
, такое, что  .
.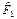 :
: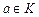 в множество
в множество  , где
, где 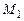 состоит из двух элементов
состоит из двух элементов 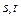 ;
;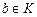 в множество
в множество 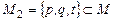 ;
;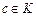 в элемент
в элемент 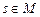 .
.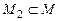 ,
, ,
,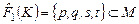 .
.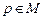 состоит из одного элемента
состоит из одного элемента 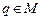 также состоит из одного элемента
также состоит из одного элемента 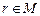 служит пустое множество
служит пустое множество 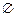 ,
,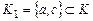 ,
, представляет множество
представляет множество 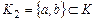 .
.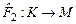 , действующее так:
, действующее так:  .
.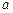 является один элемент
является один элемент 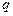 ); переводит элемент
); переводит элемент 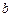 является один элемент
является один элемент  ); переводит элемент
); переводит элемент  является один элемент
является один элемент  .
.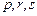 - пустые множества.
- пустые множества.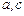 .
. , где
, где - множество всех векторов в трехмерном пространстве,
- множество всех векторов в трехмерном пространстве, 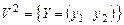 - множество всех векторов на плоскости,
- множество всех векторов на плоскости, . (1)
. (1) и прообраз вектора
и прообраз вектора  .
.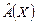 подставим координаты вектора
подставим координаты вектора 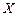 в формулы (1):
в формулы (1):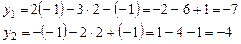
 .
.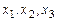 .
. ,
, 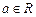 .
.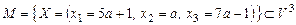 , зависящее от одного параметра
, зависящее от одного параметра 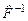 .
. ,
, 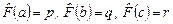 .
. 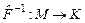 действует так:
действует так: .
.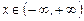 ,
,  . Отображение
. Отображение 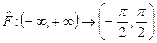 , определенное по правилу
, определенное по правилу 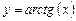 , является взаимно однозначным отображением. Обратным отображением
, является взаимно однозначным отображением. Обратным отображением  будет закон:
будет закон: 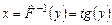 .
.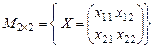 - множество всех квадратных матриц второго порядка.
- множество всех квадратных матриц второго порядка. , заданное по правилу
, заданное по правилу 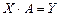 , где
, где 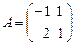 , однозначно определяет по заданной матрице
, однозначно определяет по заданной матрице  ).
).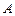 отличен от нуля, то по заданному образу (матрице
отличен от нуля, то по заданному образу (матрице  . Следовательно,
. Следовательно,  на множество
на множество 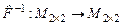 действует так:
действует так: 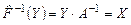 .
.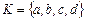 ,
, 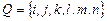 . Даны два однозначных отображения
. Даны два однозначных отображения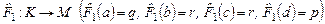 и
и  .
.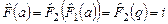 ;
;  ;
; 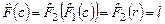 ;
; . Следовательно,
. Следовательно, 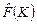 - множество из трех элементов
- множество из трех элементов  .
. называется оператором, если
называется оператором, если 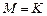 (т.е.
(т.е. 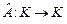 ).
). ; (2)
; (2) , (3)
, (3)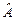 называют линейным отображением.
называют линейным отображением.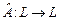 , определенный на линейном пространстве
, определенный на линейном пространстве 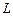 и обладающий свойствами (2), (3), называется линейным оператором.
и обладающий свойствами (2), (3), называется линейным оператором.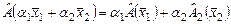
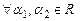 и
и 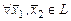 . (4)
. (4)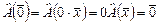 . Следовательно, любой линейный оператор
. Следовательно, любой линейный оператор 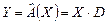 , где
, где  . (5)
. (5)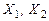 - два произвольных вектора из пространства
- два произвольных вектора из пространства 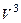 и
и 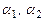 - два произвольных числа. На основании равенства (5), выводим
- два произвольных числа. На основании равенства (5), выводим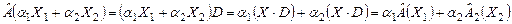 .
.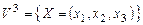 ,
, 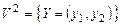 ,
,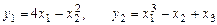 , (6)
, (6)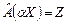 .
. и
и 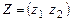 , то согласно закону (6)
, то согласно закону (6)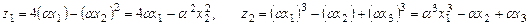 . (7)
. (7) , где
, где 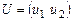 .
. . (8)
. (8) и
и 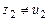 . Следовательно,
. Следовательно,  . Значит,
. Значит, 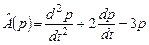 , действующее в пространстве многочленов
, действующее в пространстве многочленов  , является линейным оператором
, является линейным оператором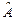 - оператор.
- оператор. 
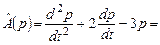
 - оператор.
- оператор.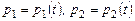 - два произвольных многочлена из пространства
- два произвольных многочлена из пространства 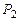 и
и 
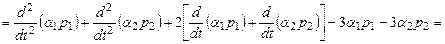

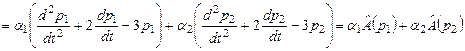 .
.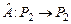 - линейный оператор.
- линейный оператор.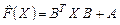 , (где
, (где 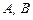 -заданные квадратные матрицы второго порядка), действующее в пространстве матриц
-заданные квадратные матрицы второго порядка), действующее в пространстве матриц  , линейным оператором?
, линейным оператором? - оператор.
- оператор.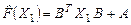 ,
, 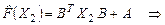
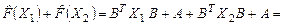
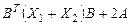 .
.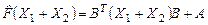 .
.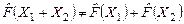 . Не выполнение свойства (2) означает, что заданный оператор
. Не выполнение свойства (2) означает, что заданный оператор 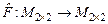 не является линейным.
не является линейным. , определенное формулой
, определенное формулой 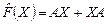 , где
, где  , является линейным оператором.
, является линейным оператором. - произвольные матрицы из множества
- произвольные матрицы из множества  - произвольные числа.
- произвольные числа.
 .
.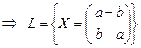 - линейное подпространство в пространстве
- линейное подпространство в пространстве 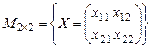 .
. .
.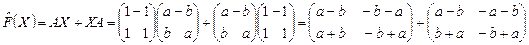 =
=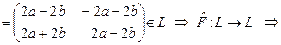
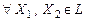 и
и 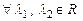


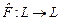 - линейный оператор, действующий в линейном пространстве
- линейный оператор, действующий в линейном пространстве  ;
;  - базис пространства
- базис пространства 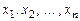 - координаты вектора
- координаты вектора 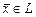 в этом базисе
в этом базисе 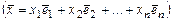 ;
; 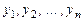 - координаты вектора
- координаты вектора 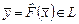 , являющегося образом вектора
, являющегося образом вектора 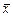 . Тогда действие оператора
. Тогда действие оператора 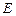 определяется матричным равенством
определяется матричным равенством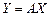 , где
, где 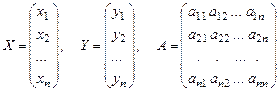 . (9)
. (9) - первый столбец матрицы
- первый столбец матрицы 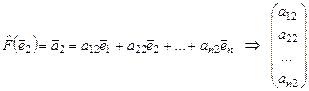 - второй столбец матрицы
- второй столбец матрицы 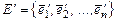 и
и  - координаты вектора
- координаты вектора 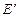 ;
;  - координаты вектора
- координаты вектора  в базисе
в базисе 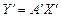 , (10)
, (10) .
. - матрицей линейного оператора
- матрицей линейного оператора  , (11)
, (11)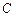 - матрица перехода от базиса
- матрица перехода от базиса 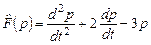 , в стандартном базисе
, в стандартном базисе 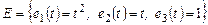 . С помощью найденной матрицы
. С помощью найденной матрицы 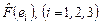 элементов базиса
элементов базиса 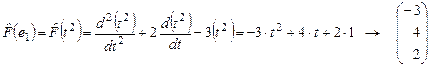 - 1-й столбец матрицы
- 1-й столбец матрицы 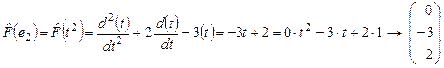 - 2-й столбец матрицы
- 2-й столбец матрицы 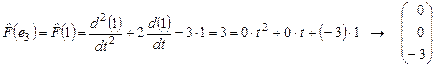 - 3-й столбец матрицы
- 3-й столбец матрицы  .
. .
. .
.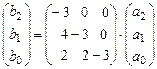 .
.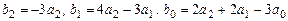 в базисе
в базисе 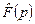 функции
функции 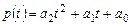 . По координатам
. По координатам  восстанавливаем явное выражение для
восстанавливаем явное выражение для  .
.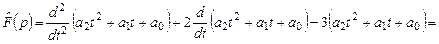
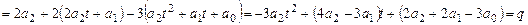 .
.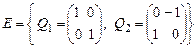 и
и  .
. линейного оператора
линейного оператора 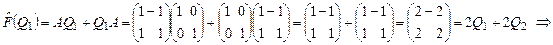
 - 1-й столбец матрицы
- 1-й столбец матрицы 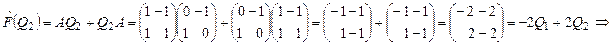
 - 2-й столбец матрицы
- 2-й столбец матрицы 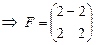 - матрица линейного оператора
- матрица линейного оператора  линейного оператора
линейного оператора  найдем с помощью формулы (11), которая в нашем случае примет вид
найдем с помощью формулы (11), которая в нашем случае примет вид  .
.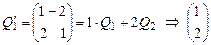 - 1-й столбец
- 1-й столбец 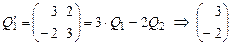 - 2-й столбец
- 2-й столбец 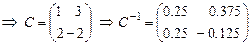 .
. .
.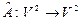 , если в базисе
, если в базисе 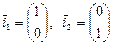 действие этого оператора производится по формулам
действие этого оператора производится по формулам 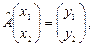 где
где 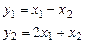 . Найти матрицу этого оператора в базисе
. Найти матрицу этого оператора в базисе  и в базисе
и в базисе 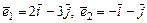 .
.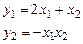 является оператором, но не является линейным оператором. Найти образ вектора
является оператором, но не является линейным оператором. Найти образ вектора 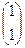 и все прообразы вектора
и все прообразы вектора 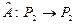 ,
, 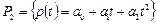 ,
,  является линейным оператором и найти матрицу этого оператора в стандартном базисе
является линейным оператором и найти матрицу этого оператора в стандартном базисе 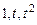 и базисе
и базисе 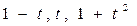 .
.