
|
|
Знакопеременные, знакопостоянные и знакоопределенные квадратичные формы. Критерий Сильвестра.Занятие 10 (Фдз 11). 10.1. Знакопеременные, знакопостоянные квадратичные формы (определения, примеры). Их канонический и нормальный вид, индексы и ранг. Знакоопределенные (положительно и отрицательно определенные) квадратичные формы. Их канонический и нормальный вид. Индексы и ранг знакоопределенной формы. 10.2. Критерий Сильвестра положительной (отрицательной) определенности квадратичной формы. 10.3. Применение критерия Сильвестра при нахождении экстремумов функции нескольких переменных.
10.1. Квадратичная форма (или неопределенной), если существуют два набора координат
Нормальный вид знакопеременной квадратичной формы такой:
Квадратичная форма называется положительной, если для любого набора координат Нормальный вид неотрицательной квадратичной формы такой:
Квадратичная форма называется отрицательной, если для любого набора координат Нормальный вид неположительной квадратичной формы такой:
Положительные и отрицательные квадратичные формы называются знакопостоянными(их также называют полуопределенными).
Квадратичная форма называется положительно определенной, если для любого нетривиального набора координат Нормальный вид положительно определенной квадратичной формы такой:
Квадратичная форма называется отрицательно определенной, если для любого нетривиального набора координат Нормальный вид отрицательно определенной квадратичной формы такой:
Положительно и отрицательно определенные квадратичные формы называются знакоопределенными (или определенными).
Приведем примеры. 1) 2) 3) 4) 5)
В данных примерах рассмотрены достаточно простые (для исследования на знак) квадратичные формы. В общем случае, исследование знака квадратичной формы можно провести только после приведения квадратичной формы к каноническому виду.
Пример 1. Исследовать на знак квадратичную форму Решение. Данная квадратичная форма приводится к следующему каноническому виду (см. пример 1 из занятия 9):
Пример 2. Исследовать на знак квадратичную форму Решение. Данная квадратичная форма приводится к следующему каноническому виду (см. пример 2 из занятия 9):
Пример 3. Исследовать на знак квадратичную форму
Решение. Данная квадратичная форма приводится к следующему каноническому виду (см. пример 3 из занятия 9):
Пример 4. Исследовать на знак квадратичную форму
Решение. Данная квадратичная форма приводится к следующему каноническому виду (см. пример 4 из занятия 9):
Пример 5. Исследовать на знак квадратичную форму
Решение. Методом Лагранжа приведем квадратичную форму к каноническому виду.
10.2.При исследовании квадратичной формы на положительную или отрицательную определенность вместо метода приведения квадратичной формы к каноническому виду часто используют критерий Сильвестра. Рассмотрим матрицу Вычислим все ее угловые определители: Справедлива следующая теорема (критерий Сильвестра). 1. Квадратичная форма 2. Квадратичная форма
Пример 6. С помощью критерия Сильвестра исследовать на знакоопределенность квадратичную форму Решение.
Пример 7. С помощью критерия Сильвестра исследовать на знакоопределенность квадратичную форму Решение.
Пример 8. С помощью критерия Сильвестра исследовать на знакоопределенность квадратичную форму Решение.
вывод: данная квадратичная форма является отрицательно определенной.
10.3.Критерий Сильвестра используется также при поиске экстремумов функции нескольких переменных. Приведем алгоритм нахождения экстремумов функции 1. Из системы уравнений 2. Вычисляем все частные производные второго порядка и составляем из них матрицу
3. Подставим координаты стационарной точки 1) если 2) если 3) если
Пример 9. Найти экстремумы функции Решение. ОДЗ (область допустимых значений):
Теперь вычислим элементы
В точке
Пример 10. Найти экстремумы функции Решение. ОДЗ (область допустимых значений):
Учитывая ОДЗ, из уравнения Если Следовательно, функция Теперь вычислим элементы
1) В точке
2) В точке
________________________________________________________________________
Домашнее задание. 1. С помощью критерия Сильвестра исследовать на положительную (отрицательную) определенность следующие квадратичные формы. Если квадратичная форма не является знакоопределенной, то методом Лагранжа привести ее к каноническому виду, по которому определить является ли она знакопеременной или знакопостоянной. 1.1. 1.2. 1.3. 2. Исследовать на экстремум следующую функцию (с применением критерия Сильвестра).

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 называется знакопеременной
называется знакопеременной и
и  таких, что
таких, что и
и  .
. .
. - ее инварианты. Ранг
- ее инварианты. Ранг  .
.
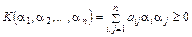 , при этом существует нетривиальный набор
, при этом существует нетривиальный набор  такой, что
такой, что  .
. .
.  - ее инварианты. Ранг
- ее инварианты. Ранг  .
. , при этом существует нетривиальный набор
, при этом существует нетривиальный набор  .
.  - ее инварианты. Ранг
- ее инварианты. Ранг  .
.
 .
. .
. 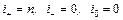 - ее инварианты. Ранг
- ее инварианты. Ранг  .
. .
. .
.  - ее инварианты. Ранг
- ее инварианты. Ранг  - знакопеременная (неопределенная) квадратичная форма, т.к.
- знакопеременная (неопределенная) квадратичная форма, т.к.  и
и  .
. - положительная (полуопределенная) квадратичная форма. Действительно,
- положительная (полуопределенная) квадратичная форма. Действительно,  можно переписать в виде
можно переписать в виде  . Отсюда видно, что
. Отсюда видно, что  и
и  .
. - отрицательная (полуопределенная) квадратичная форма. Действительно,
- отрицательная (полуопределенная) квадратичная форма. Действительно,  . Отсюда видно, что
. Отсюда видно, что  и
и  .
. - положительно определенная квадратичная форма. Действительно,
- положительно определенная квадратичная форма. Действительно,  и
и  только когда
только когда  .
. - отрицательно определенная квадратичная форма. Действительно,
- отрицательно определенная квадратичная форма. Действительно,  .
. . Отсюда выводится, что
. Отсюда выводится, что 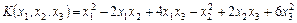 .
.
 - знакопеременная квадратичная форма.
- знакопеременная квадратичная форма. .
.

 .
.

 - знакопеременная квадратичная форма.
- знакопеременная квадратичная форма. .
.
 .
. .
. .
.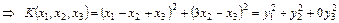 - нормальный вид квадратичной формы.
- нормальный вид квадратичной формы.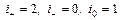 - инварианты формы
- инварианты формы 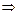
 - положительная (полуопределенная) форма.
- положительная (полуопределенная) форма. квадратичной формы
квадратичной формы  и
и .
. квадратичной формы строго положительны, т.е.
квадратичной формы строго положительны, т.е.  .
. .
. .
. - матрица кв. формы
- матрица кв. формы  . Из критерия Сильвестра следует вывод: данная квадратичная форма является положительно определенной.
. Из критерия Сильвестра следует вывод: данная квадратичная форма является положительно определенной. .
. - матрица кв. формы
- матрица кв. формы  . Согласно критерию Сильвестра данная квадратичная форма не является ни положительно, ни отрицательно определенной. Следовательно, эта форма либо знакопостоянна, либо знакопеременна. Получить точный ответ можно после приведения этой квадратичной формы к каноническому виду.
. Согласно критерию Сильвестра данная квадратичная форма не является ни положительно, ни отрицательно определенной. Следовательно, эта форма либо знакопостоянна, либо знакопеременна. Получить точный ответ можно после приведения этой квадратичной формы к каноническому виду. .
. - матрица кв. формы
- матрица кв. формы  . Из критерия Сильвестра следует
. Из критерия Сильвестра следует .
. находим стационарные точки (критические точки на экстремум):
находим стационарные точки (критические точки на экстремум):  .
. ,
, .
.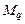 в матрицу
в матрицу  , которая является матрицей квадратичной формы
, которая является матрицей квадратичной формы  . Эта квадратичная форма совпадает с дифференциалом второго порядка функции
. Эта квадратичная форма совпадает с дифференциалом второго порядка функции  .
. .
. .
.
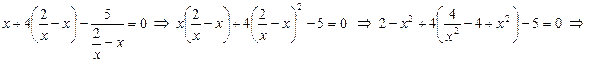
 .
. .
. . Это значение
. Это значение  не удовлетворяет ОДЗ. Следовательно, функция
не удовлетворяет ОДЗ. Следовательно, функция  имеет только одну стационарную точку
имеет только одну стационарную точку  .
. матрицы
матрицы  .
. .
. :
:  .
.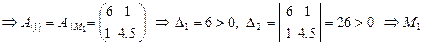 - точка минимума.
- точка минимума.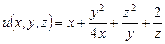 .
. .
.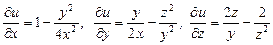 .
.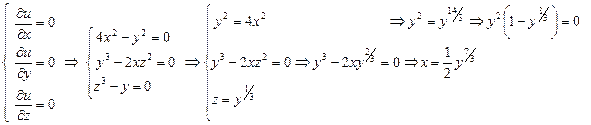
 находим
находим  .
.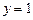 , то
, то  . Если
. Если 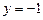 , то
, то  .
. имеет две стационарные точки
имеет две стационарные точки  .
. .
. ,
, .
. :
:  ,
, 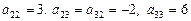 .
. .
.
 :
:  ,
,  .
. .
.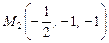 - точка локального максимума функции
- точка локального максимума функции  ,
,  .
. .
. .
. .
.