Линейные пространства (повторение основных положений линейных пространств).
Занятие 0 (Фдз 1).
0.1. Повторение основных понятий и терминов, связанных с линейными пространствами (линейная зависимость, независимость системы векторов; базис и размерность линейного пространства; разложение вектора по базису; линейная оболочка системы векторов).
0.1. Вспомним основные определения, связанные с линейными пространствами.
Пусть 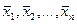 - набор элементов (система векторов) из линейного пространства - набор элементов (система векторов) из линейного пространства  . .
1) Система 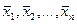 - линейно независимая система, если их линейная комбинация - линейно независимая система, если их линейная комбинация  равна нулевому элементу равна нулевому элементу  только при тривиальном наборе чисел: только при тривиальном наборе чисел: 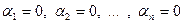 . .
Если же существует нетривиальный набор чисел 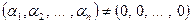 , для которого , для которого  , то система , то система 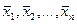 является линейно зависимой. является линейно зависимой.
2) Если система 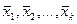 является максимальной линейно независимой системой в линейном пространстве является максимальной линейно независимой системой в линейном пространстве  (т.е. присоединение к ней любого вектора (т.е. присоединение к ней любого вектора  приводит к тому, что система приводит к тому, что система 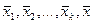 становится линейно зависимой), то система становится линейно зависимой), то система 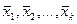 называется базисом пространства называется базисом пространства  . .
В этом случае любой вектор  можно единственным образом представить линейной комбинацией можно единственным образом представить линейной комбинацией 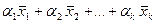 на векторах базиса, т.е. на векторах базиса, т.е.
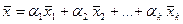 . (1) . (1)
Это равенство называется разложением вектора  по базису по базису 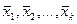 , а набор чисел , а набор чисел
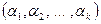 - координатами вектора - координатами вектора  в базисе в базисе 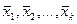 . .
3) Число векторов в любом базисе линейного пространства  всегда одно и то же и называется размерностью пространства всегда одно и то же и называется размерностью пространства  . .
4) Система 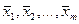 называется полной системой в линейном пространстве называется полной системой в линейном пространстве  , если любой вектор , если любой вектор  можно разложить по векторам по векторам можно разложить по векторам по векторам 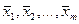 , т.е. , т.е.  . Полная система может быть линейно зависимой системой. . Полная система может быть линейно зависимой системой.
Если же полная система 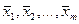 является еще и линейно независимой, то такая система – базис пространства является еще и линейно независимой, то такая система – базис пространства  (второе определение базиса). (второе определение базиса).
5) Множество всех векторов  называется линейной оболочкой на векторах называется линейной оболочкой на векторах 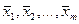 . Линейная оболочка является линейным подпространством в пространстве . Линейная оболочка является линейным подпространством в пространстве  или совпадает с линейным пространством или совпадает с линейным пространством  . .
Перейдем к примерам.
Рассмотрим систему 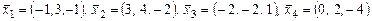 из линейного пространства из линейного пространства 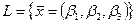 . .
Пример 1. Показать, что система 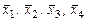 линейно зависима. линейно зависима.
Решение.
  . .
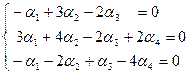 . (2) . (2)
Полученную линейную систему уравнений для неизвестных величин 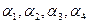 решим методом Гаусса, используя матрицу решим методом Гаусса, используя матрицу 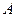 системы. системы.
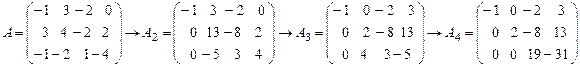
Здесь проведены следующие действия.
1) В матрице 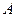 ко 2-й строке прибавлена 1-я строка, умноженная на 3, и из 3-й строки вычтена 1-я строка. В результате получена матрица ко 2-й строке прибавлена 1-я строка, умноженная на 3, и из 3-й строки вычтена 1-я строка. В результате получена матрица 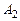 . .
2) В матрице 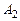 поменяли местами 2-й и 4-й столбцы, т.е. переставили местами неизвестные поменяли местами 2-й и 4-й столбцы, т.е. переставили местами неизвестные  и и  . В результате получили матрицу . В результате получили матрицу 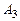 . .
3) В матрице 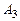 из 3-й строки вычли 2-ю строку, умноженную на (-2). В результате получили матрицу из 3-й строки вычли 2-ю строку, умноженную на (-2). В результате получили матрицу  треугольного вида, которая приводит к следующей системе: треугольного вида, которая приводит к следующей системе:
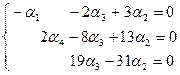 . .
В этой системе (эквивалентной исходной системе (2))  - свободная неизвестная, а - свободная неизвестная, а 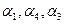 - базисные неизвестные. Положим - базисные неизвестные. Положим  , где , где 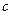 - произвольное число. Из третьего, второго и первого уравнений системы последовательно находим: - произвольное число. Из третьего, второго и первого уравнений системы последовательно находим:
 , ,
 , ,
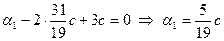 . .
Таким образом, общее решение системы (2) представимо в виде:
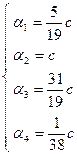 , где , где  . .
Отсюда сразу же выводится существование нетривиальных решений системы. Например, при  получаем получаем 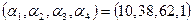 . .
Следовательно,  . Это доказывает линейную зависимость данной системы векторов . Это доказывает линейную зависимость данной системы векторов 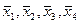 . .
Пример 2. Показать, что система 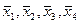 - полная система в пространстве - полная система в пространстве 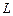 . .
Решение.
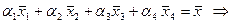
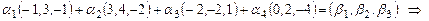
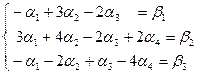 (3) (3)
В этой системе неизвестными являются 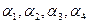 , а , а  - произвольные заданные числа. Решим систему (3) методом Гаусса, используя расширенную матрицу - произвольные заданные числа. Решим систему (3) методом Гаусса, используя расширенную матрицу  системы. Преобразования над матрицей системы. Преобразования над матрицей  полностью совпадают с преобразованиями матрицы полностью совпадают с преобразованиями матрицы 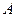 из примера 1, проведенными при доказательстве линейной зависимости системы из примера 1, проведенными при доказательстве линейной зависимости системы 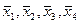 . .
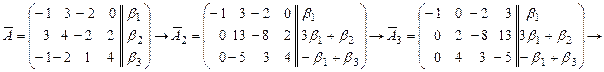
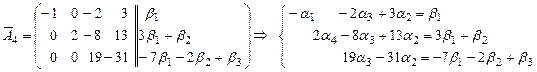 (4) (4)
В полученной системе  является свободной неизвестной, а является свободной неизвестной, а 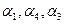 - базисными неизвестными. Положим - базисными неизвестными. Положим  , где , где 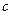 - произвольное число. Из третьего, второго и первого уравнений системы (4) последовательно находим - произвольное число. Из третьего, второго и первого уравнений системы (4) последовательно находим
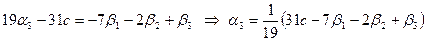 , ,
 , ,
 . .
Таким образом, установлено, что любой вектор  может быть представлен в виде может быть представлен в виде  , т.е. разложен по системе векторов , т.е. разложен по системе векторов 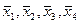 . Значения коэффициентов . Значения коэффициентов 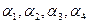 разложения таковы: разложения таковы:
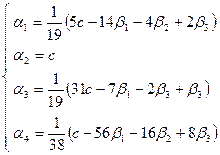 , где , где  . (5) . (5)
Следовательно, система 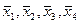 - полная в пространстве - полная в пространстве  . Заметим еще, что значения . Заметим еще, что значения 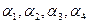 зависят не только от координат зависят не только от координат  вектора вектора  , но и от параметра , но и от параметра 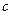 , который показывает, что существует бесконечно много различных разложений вектора , который показывает, что существует бесконечно много различных разложений вектора  по заданной системе по заданной системе 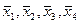 . Проведенное решение доказывает также, что линейная оболочка на векторах . Проведенное решение доказывает также, что линейная оболочка на векторах 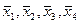 совпадает со всем линейным пространством совпадает со всем линейным пространством  . .
Пример 3. Выделить из системы 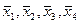 подсистемы векторов, которые служат базисами пространства подсистемы векторов, которые служат базисами пространства 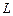 . .
Решение.
Так как система векторов  представляет стандартный базис пространства представляет стандартный базис пространства 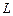 , то сразу можно сказать, что размерность пространства , то сразу можно сказать, что размерность пространства 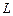 равна трем равна трем 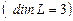 , и любой базис этого пространства состоит из трех линейно независимых векторов. Возьмем три первых вектора , и любой базис этого пространства состоит из трех линейно независимых векторов. Возьмем три первых вектора  . Исследуем их линейную зависимость (независимость). . Исследуем их линейную зависимость (независимость).
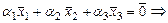 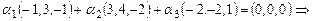 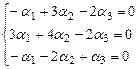 . .
Главный определитель  полученной линейной однородной системы (состоящий из координат векторов полученной линейной однородной системы (состоящий из координат векторов  , записанных столбцами) отличен от нуля. Действительно, , записанных столбцами) отличен от нуля. Действительно,
 . .
Согласно правилу Крамера, система имеет только одно решение. Это решение
 . Следовательно, система векторов . Следовательно, система векторов  линейно независима. С учетом выводов в начале решения, заключаем: подсистема линейно независима. С учетом выводов в начале решения, заключаем: подсистема  из системы из системы 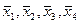 является базисом пространства является базисом пространства 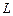 . .
Совершенно аналогично доказывается, что тройки векторов: 1) 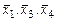 ; ;
2)  ; 3) ; 3) 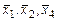 тоже будут базисами пространства тоже будут базисами пространства 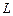 . Для этого достаточно проверить, что определители из координат векторов указанных троек отличны от нуля. Приведем эти определители и их значения. . Для этого достаточно проверить, что определители из координат векторов указанных троек отличны от нуля. Приведем эти определители и их значения.
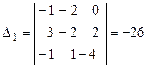 , , 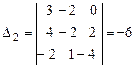 , , 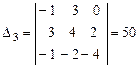 . .
Пример 4. Найти координаты вектора  в базисе в базисе  . .
Решение.
Запишем разложение вектора  по векторам по векторам  , из которого найдем искомые координаты. , из которого найдем искомые координаты.
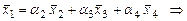 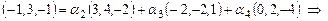
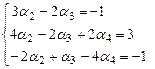 . .
Полученную систему решаем методом Гаусса, проводя соответствующие преобразования расширенной матрицы  системы. системы.
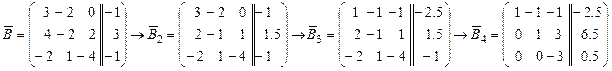 . .
Здесь над матрицей  проделаны следующие действия. проделаны следующие действия.
1) 2-ю строку матрицы  умножили на умножили на 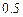 , в результате получили матрицу , в результате получили матрицу 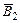 . .
2) У матрицы 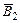 из 1-й строки вычли 2-ю строчку. Получили матрицу из 1-й строки вычли 2-ю строчку. Получили матрицу 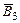 . .
2) В матрице 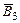 к 3-й строке прибавили 2-ю строку и ко 2-й строке прибавили 1-ю строку, умноженную к 3-й строке прибавили 2-ю строку и ко 2-й строке прибавили 1-ю строку, умноженную 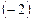 . .
По матрице 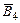 выписываем соответствующую линейную систему и решаем ее. выписываем соответствующую линейную систему и решаем ее.
  в базисе в базисе  . .
________________________________________________________________________________
Домашнее задание.
1. Исследовать на линейную зависимость систему матриц
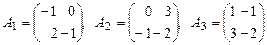 . .
2. Доказать, что множество  является линейным подпространством в пространстве является линейным подпространством в пространстве  . Найти базис и размерность подпространства . Найти базис и размерность подпространства 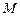
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


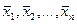 - набор элементов (система векторов) из линейного пространства
- набор элементов (система векторов) из линейного пространства  .
. равна нулевому элементу
равна нулевому элементу  только при тривиальном наборе чисел:
только при тривиальном наборе чисел: 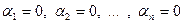 .
.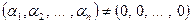 , для которого
, для которого  , то система
, то система 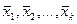 является максимальной линейно независимой системой в линейном пространстве
является максимальной линейно независимой системой в линейном пространстве  приводит к тому, что система
приводит к тому, что система 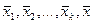 становится линейно зависимой), то система
становится линейно зависимой), то система 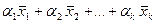 на векторах базиса, т.е.
на векторах базиса, т.е.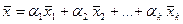 . (1)
. (1) по базису
по базису 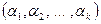 - координатами вектора
- координатами вектора 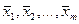 называется полной системой в линейном пространстве
называется полной системой в линейном пространстве  . Полная система может быть линейно зависимой системой.
. Полная система может быть линейно зависимой системой.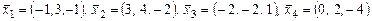 из линейного пространства
из линейного пространства 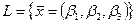 .
.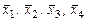 линейно зависима.
линейно зависима.
 .
.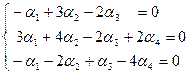 . (2)
. (2)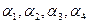 решим методом Гаусса, используя матрицу
решим методом Гаусса, используя матрицу 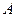 системы.
системы.
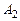 .
. и
и  . В результате получили матрицу
. В результате получили матрицу 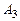 .
. треугольного вида, которая приводит к следующей системе:
треугольного вида, которая приводит к следующей системе: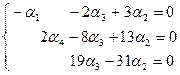 .
.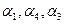 - базисные неизвестные. Положим
- базисные неизвестные. Положим  , где
, где 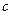 - произвольное число. Из третьего, второго и первого уравнений системы последовательно находим:
- произвольное число. Из третьего, второго и первого уравнений системы последовательно находим: ,
, ,
,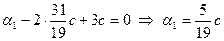 .
.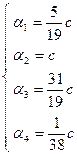 , где
, где  .
. получаем
получаем 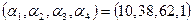 .
. . Это доказывает линейную зависимость данной системы векторов
. Это доказывает линейную зависимость данной системы векторов 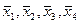 .
.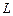 .
.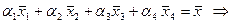
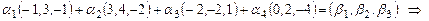
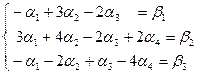 (3)
(3) - произвольные заданные числа. Решим систему (3) методом Гаусса, используя расширенную матрицу
- произвольные заданные числа. Решим систему (3) методом Гаусса, используя расширенную матрицу  системы. Преобразования над матрицей
системы. Преобразования над матрицей 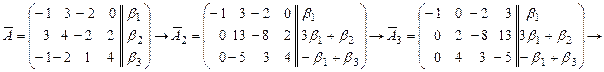
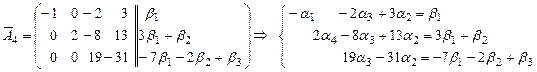 (4)
(4)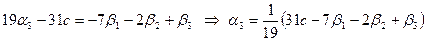 ,
, ,
, .
. может быть представлен в виде
может быть представлен в виде  , т.е. разложен по системе векторов
, т.е. разложен по системе векторов 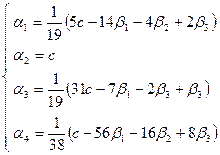 , где
, где  представляет стандартный базис пространства
представляет стандартный базис пространства 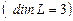 , и любой базис этого пространства состоит из трех линейно независимых векторов. Возьмем три первых вектора
, и любой базис этого пространства состоит из трех линейно независимых векторов. Возьмем три первых вектора  . Исследуем их линейную зависимость (независимость).
. Исследуем их линейную зависимость (независимость).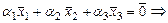
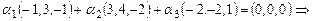
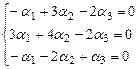 .
. полученной линейной однородной системы (состоящий из координат векторов
полученной линейной однородной системы (состоящий из координат векторов  .
. . Следовательно, система векторов
. Следовательно, система векторов 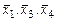 ;
; ; 3)
; 3) 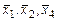 тоже будут базисами пространства
тоже будут базисами пространства 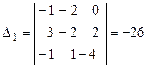 ,
, 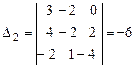 ,
, 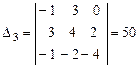 .
. в базисе
в базисе 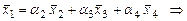
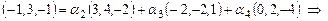
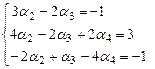 .
. системы.
системы.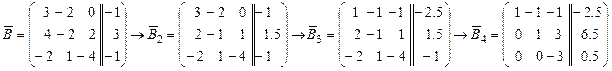 .
.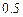 , в результате получили матрицу
, в результате получили матрицу 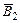 .
.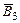 .
.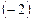 .
.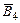 выписываем соответствующую линейную систему и решаем ее.
выписываем соответствующую линейную систему и решаем ее.
 в базисе
в базисе 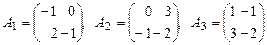 .
. является линейным подпространством в пространстве
является линейным подпространством в пространстве  . Найти базис и размерность подпространства
. Найти базис и размерность подпространства