
|
|
Решение систем линейных алгебраических уравнений методом исключения ГауссаМетоды вычислительной математики Табулирование функций Данная задача широко используется во многих дисциплинах. Обычно функции, описывающие какой-либо процесс, весьма громоздки и создание таблиц их значений требует большого объема вычислений. Рассмотрим два случая табулирования функции: 1. С постоянным шагом изменения аргументов. 2. С произвольным набором значений аргумента. Алгоритм реализуется путем организации какого-либо цикла. Пример 1. Вычислить значения функции при Текст программы: format short clc a=1.1; disp(['Таблица значений функции']) %Задается начальное значение x, шаг dx, конечное значение x x=1; dx=0.5; while x<=4+dx if x<=2 y=3*x-3.87*sin(a)-log(2+x); else y=14-exp(x); end disp([x,y]) x=x+dx; end Результаты вычислений: Таблица значений функции 1.0000 -1.5476 1.5000 -0.2017 2.0000 1.1647 2.5000 1.8175 3.0000 -6.0855 3.5000 -19.1155 4.0000 -40.5982 4.5000 -76.0171 Пример 2. Вычислить и вывести на экран значения функции
При
Цикл организуется для одномерного массива. Текст программы: format short clc a=1.35;b=0.98; x(1)=12.8; x(2)=23.4; x(3)=27.2; x(4)=17.8; x(5)=16.3; x(6)=14.9; disp(['Таблица значений функции']) for i=1:6 y(i)=(1+sin(b^2+x(i)^2)^2)/(a^2+x(i)^2)^(1/3); disp([x(i) y(i)]) end Результаты вычислений: Таблица значений функции 12.8000 0.3609 23.4000 0.2327 27.2000 0.1473 17.8000 0.1800 16.3000 0.1771 14.9000 0.1658 Определение корней полинома
Если в полиноме отсутствует степень при неизвестном, то в векторе значений коэффициентов ставится 0. Пример. Найти корни полинома: Построим график функции >> x=-2:0.1:1; >> y=4*x.^4-7*x.^2+11*x-1 ; >> plot(x,y) >> grid on Решение >> p=[4 0 -7 11 -1]; >> roots(p) ans = -1.8253 0.8642 + 0.8169i 0.8642 - 0.8169i 0.0968 Отсюда видно, что эта функция определяет как вещественные, так и комплексные корни полиномов. Исследование функций Ряд функций системы MATLAB предназначен для работы с функциями. Под функциями понимаются как встроенные функции, например Может использоваться также класс анонимных функций, задаваемых с помощью символа @, например: >> fe=@exp; Такие функции вычисляются с помощью функции >> fe=@exp; >> feval(fe,1.0) ans = 2.7183 Методы отделения корней уравнений с одной переменной Пример.Отделить корни трансцендентного Решение. Создадим файл Func.m , содержащий описание функции Файл Func.m. function z=Func(x) z=x.^2-sin(x)-1; end Построим график функции
>> plot(x, Func(x)); grid on Из рисунка видно, что функция имеет два корня: Решение уравнений, нахождение максимума или минимума функции одной или нескольких переменных осуществляется вызовом встроенных функций MatLab. Число аргументов встроенных функций может быть различным, в зависимости от требуемого вида результата. Для работы с ними необходимо предварительно написать собственную файл-функцию для вычисления исследуемой функции. Решение уравнений MATLAB можно использовать для решения алгебраических и трансцендентных уравнений и систем уравнений, заданных в виде массива символьных выражений. Решение алгебраических и трансцендентных уравнений в среде MATLAB осуществляется с помощью следующих встроенных функций: Решение уравнений при помощи функций Функция
Пример: >> fsolve('0.25*x+sin(x)-1',0:10 ) ans = Columns 1 through 6 0.8905 0.8905 2.8500 2.8500 2.8500 5.8128 Columns 7 through 11 5.8128 5.8128 5.8128 10.7429 10.7429 Функция
где:
Функция Пример. Пусть необходимо решить следующее уравнение: Программа решения уравнения имеет вид: >> solve('x^2-sin(x)-1=0') После нажатия клавиши <Enter> получим следующее решение: >> solve('x^2-sin(x)-1=0') ans = matrix([[-0.63673265080528201088799090383828]]) Решение уравнений при помощи функции Функция
где:
ПримерНеобходимо найти корни уравнения Решение: >> [x,f,e_flag,inform]=fzero('x^2-sin(x)-1',[-1, 0]) x = -0.636732650805282 f = e_flag = inform = intervaliterations: 0 iterations: 6 funcCount: 8 algorithm: 'bisection, interpolation' message: 'Zero found in the interval [-1, 0]'
>> [x,f,e_flag,inform]=fzero('x^2-sin(x)-1',[1, 2]) x = 1.409624004002596 f = -1.110223024625157e-016 e_flag = inform = intervaliterations: 0 iterations: 8 funcCount: 10 algorithm: 'bisection, interpolation' message: 'Zero found in the interval [1, 2]'
>> x=fzero('x^2-sin(x)-1',[1, 2]) x = 1.409624004002596 Возникает вопрос, сколько в ответе точных значащих цифр, т. е. с какой точностью найдено решение. Использование >> eps ans = 2.220446049250313e-016 Решение систем линейных алгебраических уравнений методом исключения Гаусса Пусть задана система Система уравнений в матричной форме представляется следующим образом:
где
Систему уравнений можно решить различными методами. Один из наиболее простых и эффективных методов является метод исключения Гаусса и его модификации. Алгоритм метода основан на приведении матрицы В MATLAB имеется обширный арсенал методов решения систем уравнений методом исключения Гаусса. Для этого применяются следующие операторы
Выражения
дают решения ряда систем линейных уравнений где Для решения систем линейных алгебраических уравнений в системе MATLAB существует две уникальные по своему назначению операции: \ -левое деление матриц; /- правое деление матриц. Операция левого деления матриц \ используется при решении уравнений вида
где
Для решения этого уравнения достаточно выполнить следующую операцию:
Операция левого матричного деления эквивалентна следующей операции:
Пример. Необходимо решить следующую систему уравнений:
Матрица коэффициентов A и вектор-столбец свободных членов в этой системе уравнений имеют следующий вид: format short clc A=[3 4 6; 2 5 7; 1 8 3]; B=[-5;7;11]; y=A\B inv(A)*B Решение y = -8.2075 1.5660 2.2264 ans = -8.2075 1.5660 2.2264 Здесь операция Операция правого деления матриц
где
Для решения такого уравнения достаточно выполнить следующую операцию:
или эквивалентную ей операцию:
Пример. Решить систему уравнений:
Решение format short clc A=[3 2 1; 4 5 8; 6 7 3]; B=[-5 7 11]; y=B/A B*inv(A) y = -8.2075 1.5660 2.2264 ans = -8.2075 1.5660 2.2264 -8.2075 1.5660 2.2264 Рассмотрим решение систем линейных уравнений с помощью встроенной функции
где:
Перед функцией Пример. Пусть необходимо решить следующую систему уравнений:
Программа решения системы уравнений имеет вид: >> syms x1 x2 x3; >> Y=solve('1.23*x1-3.25*x2-8.69*x3=10.33', '7.03*x1+4.81*x2+0.27*x3=-6.43', '4.49*x1-7.55*x2+12.51*x3=41.53') После нажатия клавиши <Enter> получим ответ в следующем виде: Y = x1: [1x1 sym] x2: [1x1 sym] x3: [1x1 sym] Программа задачу решила, но не выдала значения неизвестных >> Y.x1 ans = 1.6467696870844978837212332256586
>> Y.x2 ans = -3.7690989344414828576791743237764
>> Y.x3 ans = .45398138688708304769095896660916 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

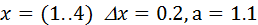



 которая возвращает вектор элементов, являющихся корнями заданного (в виде вектор - строки коэффициентов) полинома
которая возвращает вектор элементов, являющихся корнями заданного (в виде вектор - строки коэффициентов) полинома  .
.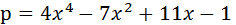
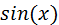 или
или 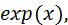 так и функции пользователя, например
так и функции пользователя, например 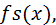 задаваемые как M- файлы функции.
задаваемые как M- файлы функции.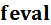 :
: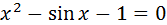 уравнения графически.
уравнения графически. и
и  .
.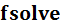 ,
, 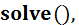

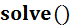 .
. , где
, где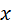 — вектор или матрица неизвестных,
— вектор или матрица неизвестных,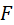 — функция, значением которой является вектор или матрица,
— функция, значением которой является вектор или матрица,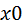 - начальное значение или интервал поиска решения.
- начальное значение или интервал поиска решения.
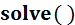 представляется в следующем виде:
представляется в следующем виде:
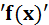 – решаемое уравнение, записанное в одиночных кавычках;
– решаемое уравнение, записанное в одиночных кавычках;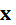 – искомое неизвестное.
– искомое неизвестное. .
.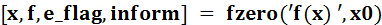
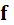 – значение невязки;
– значение невязки;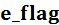 – переменная, знак которой свидетельствует о наличии корня на данном интервале ( например,
– переменная, знак которой свидетельствует о наличии корня на данном интервале ( например,  – корень существует);
– корень существует);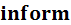 – содержит три поля с именами:
– содержит три поля с именами: (количество итераций),
(количество итераций), (количество обращений к функции
(количество обращений к функции  ), и
), и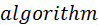 (наименование алгоритма, использованного для нахождения корня;
(наименование алгоритма, использованного для нахождения корня;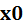 – начальное приближение или интервал поиска решения.
– начальное приближение или интервал поиска решения.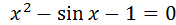 ,если известно, что корни находятся в промежутках [-1, 0] и [1, 2].
,если известно, что корни находятся в промежутках [-1, 0] и [1, 2]. с двумя аргументами приводит к нахождению корня с точностью
с двумя аргументами приводит к нахождению корня с точностью 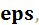 где
где 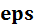 — встроенная функция MatLab, задающая точность вычислений, значение которой можно посмотреть так же, как и значения других переменных:
— встроенная функция MatLab, задающая точность вычислений, значение которой можно посмотреть так же, как и значения других переменных: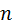 линейных алгебраических уравнений с
линейных алгебраических уравнений с 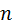 неизвестными:
неизвестными: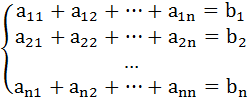
 ,
,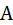 – квадратная матрица коэффициентов, размером
– квадратная матрица коэффициентов, размером 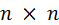 строк и столбцов;
строк и столбцов; – вектор-столбец неизвестных;
– вектор-столбец неизвестных;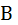 – вектор-столбец правых частей.
– вектор-столбец правых частей.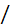

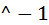
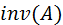
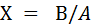



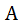 – матрица размером
– матрица размером 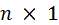 .
.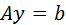 ,
, – заданная квадратная матрица коэффициентов уравнений;
– заданная квадратная матрица коэффициентов уравнений;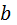 – вектор- столбец свободных членов;
– вектор- столбец свободных членов;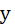 – вектор-столбец искомых переменных.
– вектор-столбец искомых переменных.

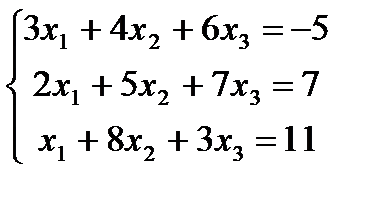
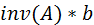 была выполнена для проверки правильности решения.
была выполнена для проверки правильности решения. позволяет решать системы уравнений вида
позволяет решать системы уравнений вида
 – вектор-строка неизвестных переменных;
– вектор-строка неизвестных переменных;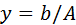
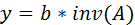


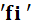 – i-е уравнение системы, i=1, 2, …, n;
– i-е уравнение системы, i=1, 2, …, n; – i-е неизвестное, i=1, 2, …, n.
– i-е неизвестное, i=1, 2, …, n. определить символьные переменные.
определить символьные переменные.
 ,
, 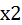 ,
,  . Для их получения необходимо воспользоваться командой
. Для их получения необходимо воспользоваться командой 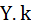 , где
, где 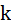 – имя неизвестного. В нашем случае решение будет иметь вид:
– имя неизвестного. В нашем случае решение будет иметь вид: