
|
|
Мобилизующее начало урока. (1 мин).Факультативное занятие по теме «Решение уравнений с модулем». Учитель математики Евдокимова Л.А. Методист Теребильникова О.В. Класс 10 «А». Цели: Образовательные: повторить понятие модуль числа, алгоритм его нахождения, изучить основные способы решения уравнений с модулем. Начать формировать умения по решению задач. Развивающие: развитие качеств научного мышления (целенаправленность, критичность), мыслительных умений (анализ, синтез, сравнение, обобщение). Воспитательные: воспитание внимания, аккуратности, алгоритмической культуры и культуры математической речи. Структура урока: Мобилизующее начало урока. (1 мин). 2. Беседа с классом с целью мотивации изучения темы. (2 мин). 3. Беседа с классом с целью актуализации знаний о модуле числа, алгоритме его нахождения. (5 мин). 4. Постановка целей урока. (2 мин). 5. Решение уравнения - примера с модулем учителем. (5 мин). 6. Решение уравнения а с модулем у доски. (10 мин). 7. Самостоятельное решение уравнений с модулем на местах. (15 мин). 8. Подведение итогов урока, постановка домашнего задания. (5 мин).
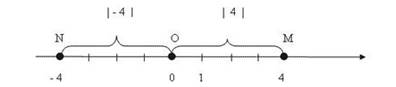
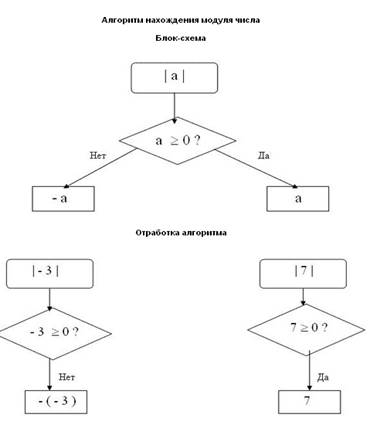
Ход урока 1. Учитель: Здравствуйте, Ребята, присаживайтесь. Давайте отметим присутствующих. 2. Учитель: Сегодня на уроке мы с вами изучим новую тему, которая называется «Решение уравнений с модулем». Подпишите тему урока. Данная тема достаточно актуальная, поскольку в ЕГЭ такие задания встречаются очень часто и оцениваются высоким баллом. 3. Учитель: А сейчас давайте вспомним, что мы с вами называем модулем числа? Учащиеся: Модулем числа называют расстояние от точки, изображающей число на координатной прямой до начала отсчета. Учитель: Хорошо, правильно. Учитель: Скажите, пожалуйста, а как мы с вами обозначаем модуль числа? Учащиеся: Модуль числа а обозначают | а|. Учитель: Правильно, молодцы. Я напоминаю вам, что термин “модуль” ввёл в 1806 г. французский математик Жорж Аргон. Учитель: | 6 | = 6, | – 6 | = 6 Учитель: Т.к. модуль числа – это расстояние, он никогда не будет отрицательным.
4. Учитель: Сегодня на уроке мы с вами изучим уравнения с модулем и способы их решения, порешаем их, а в конце урока вы получите небольшое домашнее задание. 5. Учитель: Решим уравнение: |x + 3| = 2x - 3. Учитель: Что необходимо сделать для решения уравнения? Учащиеся: Раскрыть модуль. Учитель: Правильно. А как это сделать? Учащиеся: Рассмотреть 2 случая, когда |x + 3| Учитель: Хорошо, рассмотрим первый случай. Учитель: |x + 3| x В данном случае уравнение принимает вид: x + 3 = 2x - 3, отсюда х = 6. Учитель: Скажите, пожалуйста, это решение удовлетворяет условию x Учащиеся: Да. Что отсюда следует? Учащиеся: 6 – корень данного уравнения. Учитель: Верно. Рассмотрим второй случай. Учитель: |x + 3| < 0, отсюда x < -3. Уравнение преобразуется к виду: - x - 3 = 2x - 3, х = 0. Учитель: Этот корень нам подходит? Учащиеся: Нет, поскольку он не удовлетворяет нашему условию x < -3. Учитель: Правильно, молодцы. Учитель: Запишите ответ: 6. Учитель: Что необходимо было знать, чтобы решить задачу? Учащиеся: Необходимо знать правила раскрытия модуля. Учитель: Правильно, молодцы. 4. Учитель: (вызываю ученика к доске). Решите уравнение: |x - 1| + |x - 2| = x + 3. Учитель: Как можно решить данное уравнение? Ученик: Необходимо рассмотреть каждый из случаев, аналогично предыдущему примеру. Учитель: Правильно, но мы сделаем немного по-другому. Учитель: Найди корни выражений, стоящих под знаком модуля. Ученик: 1 и 2. Учитель: Посмотрите, данное уравнение немного отличается от предыдущего. Поэтому нам с вами удобнее разбить числовую ось на 3 промежутка:
Учитель: В данном примере, нам достаточно рассмотреть каждый из этих случав. Учитель: Называй, какой случай мы рассмотрим первым? Ученик: 1) x Учитель: Оба выражения, стоящие под знаком модуля – неотрицательные на данном промежутке, какой вид примет наше уравнение? Ученик: x - 1 + x - 2 = x + 3. х = 3, данное значение удовлетворяет условию x Учитель: Хорошо, рассмотрим второй случай. 2) 1 Ученик: Первое выражение, стоящее под знаком модуля – положительно, а второе – отрицательно на данном промежутке, следовательно, уравнение примет вид: x - 1 + 2 - х = x + 3. х = 2, этот корень не удовлетворяет условию 1 Учитель: Хорошо, рассмотрим третий случай. 3) х < 1. Ученик: Оба выражения, стоящие под знаком модуля – отрицательны на рассматриваемом промежутке, исходное уравнение преобразуется к виду 1 - x + 2 - х = x + 3. х = 0 – решение этого уравнения, оно удовлетворяет условию х < 1, следовательно, и является решением исходного. Учитель: Хорошо, запиши ответ. Ученик: Ответ: 0;3. Учитель: Правильно, молодец. Учитель: Как мы решали данное задание? Учащиеся: Решая данную задачу, мы с вами нашли корни подмодульных выражений, разбили числовую ось на 3 промежутка, проверили каждый из них, и записали в ответ корни, удовлетворяющие условиям в каждом из случаев. 7. Учитель: А сейчас, вы самостоятельно решите следующие задания: 1) |x - 2| - |x + 3| = 6 2) |x + 1| + |x - 2| + |x + 3| = x + 4 8. Подведение итогов урока. Учитель: Давайте вспомним, чем мы с вами сегодня занимались на уроке? Учащиеся: Сегодня на уроке мы занимались решением уравнений с модулем, прорешали несколько разнотипных заданий. Учитель: На следующем уроке мы с вами продолжим решение уравнений с модулем, рассмотрим ещё несколько способов их решения. Постановка домашнего задания: Учитель: Запишите задание на дом: 1) |x - 8| - |x + 8| = 16. 2) |x - 1| + |x + 2| + |x - 3| = x – 4. Учитель: Урок окончен, до свидания! Учащиеся: До, свидания!

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 0 и |x + 3| < 0.
0 и |x + 3| < 0.
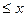 < 2
< 2