
|
|
на качество затяжного печеньяВлияние отдельных технологических факторов
Качество затяжного печенья во многом зависит от рецептуры, качества входящего в рецептуру сырья, параметров технологического процесса, а также от других многочисленных факторов. Предположим, что необходимо построить план полного факторного эксперимента ПФЭ22 для изучения влияния ферментного препарата L-цистеина в количестве от %min до %max и температуры замеса затяжного теста от 30оСmin до 50оС max на намокаемость печенья, т.е. выход процесса, обозначаемый как у.
Записываем план эксперимента:
Проверяем правильность плана в кодированном виде, т.е. его симметричность: å х1u=0; å х2u=0. Это значит, что матрица планирования ортогональна, т.е. симметрична. За выход процесса, как указывалось выше, принимаем намокаемость печенья “у”. Нужно определить количество опытов, т.е. выпечек печенья N2: имеем количество факторов – 2 (фермент + температура), значит N=2; 22=4, поэтому необходимо провести 4 выпечки (или 4 опыта). Опыты проводим в трехкратной повторности, т.е. m=3. После проведения выпечек по данным в таблице 2 и определения намокаемости печенья в % (у) экспериментальные данные заносим в таблицу 3 и вычисляем
3. Матрица планирования.
Составляем уравнение регрессии: y=B0+B1×х1+B2×х2+B1×2×х1×х2 (6) y – величина критерия оптимизации или выход процесса B0 – коэффициент, характеризующий средний выход процесса. B1, B2 – коэффициенты регрессии для изучаемых факторов, или коэффициенты пропорциональности, показывающие зависимость y от х. х – уровни изучаемых факторов.
Расчет коэффициентов уравнения.
Коэффициенты уравнения регрессии при планировании по ортогональным матрицам рассчитываются по формулам:
(т.е. все
(умножаем каждое
(умножаем каждое
(умножаем каждое Подставляем в уравнение регрессии полученные коэффициенты:
Y = + х1+ х2+ х1×х2
Полученные коэффициенты регрессии (положительные или отрицательные) представляют собой формализованное выражение степени воздействия каждого изученного фактора на процесс. Чем больше величина “B”, тем сильнее воздействует фактор на процесс. Уровни изучаемых факторов могут изменяться под влиянием неконтролируемых причин, (о чем упоминалось ранее). Чтобы убедиться, что вычисленные коэффициенты регрессии не являются результатами влияния неконтролируемых факторов, вычисляют доверительные интервалы (доверительную ошибку) В – коэффициентов по формуле:
e(bi) = t×(P ; f)×S(bi) (12) e(bi)– доверительная ошибка “В” коэффициентов; S(bi) – средняя квадратическая ошибка “B” коэффициентов; t – критерий Стьюдента, определяемый по таблицам для числа степеней свободы f=N×(m-1); (13) f=4×(3-1)=8 (доверительную вероятность или уровень значимости находим по таблице в методических указаниях) При Р=0,05 f=8; t=2,31
Критерий Стьюдента t – нормированное отклонение представляет собой отклонение тех или других вариант от их средней арифметической, выраженное в долях среднего квадратического отклонения. Если Вi>ebi, то оценка коэффициента Вi значимо отличается от нуля, если нет, то ее приравнивают к нулю, и коэффициент считается незначимым.
Проверка значимости коэффициентов.
Структура формул для определения оценок коэффициентов будет одинаковой со структурой формулы для расчета среднего арифметического. В соответствии с теоремой о дисперсии среднего можно записать:
N – характеризует общую вариацию; (m-1) - характеризует вариацию для групповых средних; m×N - характеризует вариацию для случайных отклонений.
1. Общая сумма квадратов Значок “u¼k” около знака суммы показывает, что суммирование производится по всем вариантам всех групп. 2. Суммы квадратов для групповых средних
Чтобы эта величина была того же порядка, что и первая, введем множитель “m”, т.е. число вариаций в каждой группе.
3. Сумма квадратов отклонений вариант от групповых средних внутри каждой группы, иначе говоря, для случайной вариации внутри групп.
Два знака сумм указывают, что суммирование производится дважды: внутри каждой группы, а затем по всем уровням. Для облегчения расчетов составляем промежуточную таблицу (исходные данные в таблице 3). 4. Промежуточная таблица для вычисления Sbi.
Значение подставляем в формулу (14).
S(bi)= – средняя квадратическая ошибка “B” коэффициентов. S(bi) можно вычислить и последовательно; пользуясь последней графой таблицы (4).
S(bi) - средняя квадратическая ошибка “B” коэффициентов. Находим доверительную ошибку e(bi) e=t×S(bi) e(bi) = - доверительная ошибка “B” коэффициентов = . Проверка значимости коэффициентов:
B0= B1= B2= B1,2=
Таким образом, все коэффициенты оказались значимыми, т.е. уравнение регрессии адекватно описывает процесс.
Значения х1 и х2 принимаем равными 1. Знак определяем по матрице планирования,
Полученные результаты показывают, что коэффициенты уравнения регрессии рассчитаны без арифметических ошибок. Поэтому нет смысла рассчитывать в этом случае критерий Фишера, так как:
1. Дисперсия неадекватности
В нашем случае это отношение равно нулю, так как все
2. Критерий Фишера
В том случае, если в уравнении регрессии один или два коэффициента оказались незначимыми, то Fрасч.>Fтабл., что свидетельствует о том, что уравнение регрессии неадекватно описывает процесс. Тогда нужно ставить другую серию опытов с другими интервалами варьирования.
Литература
1. Ауэрман Л.Я. «Технология хлебопекарного производства». М. «Легкая и пищевая промышленность», 1984, 386с. 2. Грачев Ю.П. «Математические методы планирования экспериментов». М. «Пищевая промышленность», 1979, 199с. 3. Пучкова Л.И. «Лабораторный практикум по технологии хлебопекарного производства» М. «Легкая и пищевая промышленность», 1982, 232с. 4. Учебно-исследовательская работа. РП, МУ для студентов 4курса (СПО); 5 курса (ДФО); 6 курса (ПФО) факультета “ТМ” для студентов спец.2703. М., 2000, 18с. 5. Энкина Л.С. «Применение статистических методов контроля для оценки технологических показателей в хлебопечении». Москва, 1971, 31с.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 для каждой серии опытов в 3х повторностях.
для каждой серии опытов в 3х повторностях.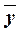
 (7)
(7) (8)
(8) складываем со знаком + и делим на N=4).
складываем со знаком + и делим на N=4). (9)
(9) (10)
(10) (11)
(11)

 .
.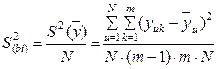 (14)
(14) (15)
(15) (16)
(16) (17)
(17)








 Если в уравнении регрессии после проверки значимости коэффициентов останутся все N коэффициентов, то проверка адекватности уравнения по критерию Фишера теряет смысл. Рассчитанный по такому уравнению выход процесса для условий u того опыта должна совпадать с величиной , принятой к расчету.
Если в уравнении регрессии после проверки значимости коэффициентов останутся все N коэффициентов, то проверка адекватности уравнения по критерию Фишера теряет смысл. Рассчитанный по такому уравнению выход процесса для условий u того опыта должна совпадать с величиной , принятой к расчету. Пример: Вернемся к вычисленному ранее уравнению регрессии, все “B” коэффициенты которого оказались значимыми, и рассчитаем выход процесса , пользуясь полученными данными.
Пример: Вернемся к вычисленному ранее уравнению регрессии, все “B” коэффициенты которого оказались значимыми, и рассчитаем выход процесса , пользуясь полученными данными. – расчетный выход процесса. Тогда:
– расчетный выход процесса. Тогда:
 (21)
(21) (22)
(22)