
|
|
Интерференция света. Когерентность колебаний и волнИзучение явления интерференции света. Кольца Ньютона Цель работы: Ознакомиться с явлением интерференции, определить радиус кривизны линзы и длину световой волны. Приборы и принадлежности: 1. Плосковыпуклая линза 2. Стеклянная пластинка 3. Микроскоп 4. Светофильтры 5. Ртутная лампа 6. Лампа накаливания. Вопросы, ответы на которые необходимо знать для выполнения работы: 1. Уравнение одномерной бегущей волны; физический смысл амплитуды и фазы колебаний. 2. Принцип суперпозиции. 3. Сущность явления интерференции. Условия максимумов и минимумов. 4. Когерентность световых волн. 5. Способы реализации когерентных источников. Кольца Ньютона - начертить ход лучей, дающих кольца Ньютона в отраженном свете. 6. Последовательность операций при выполнении работы. Введение в теорию Интерференция света. Когерентность колебаний и волн Из повседневного опыта известно, что освещенность, создаваемая двумя источниками света в любой точке экрана, где производится наблюдение, равна сумме освещенностей, получающихся от каждого источника в отдельности. Но известны также и такие оптические явления, в результате протекания которых появляются чередующиеся полосы максимальной и минимальной освещенности, т.е. происходит перераспределение потока световой энергии в пространстве. Объяснение такие явления находят в рамках электромагнитной волновой теории света. С точки зрения классической электродинамики свет представляет собой когерентные электромагнитные волны, распространяющиеся в вакууме со скоростью с = 3×108 м/с. Уравнение электромагнитной монохроматической волны имеет вид: Е=Е0cos(wt-kх) (1) где w - круговая частота колебаний электрической компоненты электромаг-нитной волны, k = E0 -амплитуда волны, l - длина волны, (wt-kх) - фаза волны. Монохроматические волны различных частот, воспринимаемые человечес-ким глазом, вызывают различные световые ощущения. Например, свет с длиной волны 550 нм воспринимается как зеленый, а с длиной волны 620 нм - как красный. Белый свет представляет собой совокупность различных монохроматических волн. Интерференциейназывается явление, возникающее при наложении волн и выражающееся в пространственно-периодическом изменении интенсивности результирующей волны. В тех точках пространства, куда колебания приходят в фазе или с разностью фаз, кратной 2p, интенсивность результирующей волны максимальна. В тех точках, где разность фаз колебаний равна нечетному числу p (колебания происходят в противофазе), интенсивность результирующей волны минимальна. Совокупность таких точек образует интерференционную картину. Для наблюдения интерференционной картины очевидно необходимо, чтобы разность фаз колебаний в различных точках пространства не менялась со временем.Волны с постоянной во времени разностью фаз называются когерентными. Таким образом, условием интерференции волн одной и той же длины волны является их когерентность, т.е. сохранение неизменной разности фаз за время, достаточное для наблюдения. Рассмотрим интерференцию света от двух когерентных источников света S1 и S2 (рис.1).
Уравнения монохроматических волн, посылаемых источниками S1 и S2, имеют вид: Е1=Е01cos(wt-kх1) Е2=Е02cos(wt-kх2) При малом угле W (т.е. при L»1) можно считать, что результирующая напряженность в точке М равна алгебраической сумме напряженностей, создаваемых источниками S1 и S2, т.е.
При этом амплитуда результирующего колебания в точке М: Е0= Поскольку интенсивность на экране пропорциональна квадрату амплитуды волны, то I ~ E I = I1+I2+ 2 Аргумент косинуса j = k(х1-x2) - разность фаз колебаний в точке наблюдения. Из последнего выражения видно, что в общем случае когерентных источников суммарная интенсивность не равна сумме интенсивностей, создаваемых отдельными источниками. Результат определяется разностью фаз интерферирующих волн в месте наблюдения. Эта разность фаз зависит от начальной разности фаз волн, а также от разности расстояний, пройденных волнами от источников до точки наблюдения. Максимальная интенсивность наблюдается при соs j = 1, j = ±2pm, минимальная - при соsj = -1, т.е. j = Отсюда следует,что условие максимумаинтенсивности запишется в виде: D = где m = 1,2,3,...., D-оптическая разность хода, а условие минимума интенсивности D = Число m определяет порядок максимума или минимума, m = 0 соответствует центральный (нулевой) порядок, m = 1 - первый и т.д. При распространении в вакууме разность фаз обуславливается только геометрической разностью путей (разностьюхода) x1 и x2 : ½x1-x2½=D, т.е. разностью фаз j =kD = В общем случае, если волны распространяются в разных оптических средах с показателями преломления n1 и n2, то D представляет собой оптическую разность хода D= n1x1-n2x2 (5) Рассмотренное распределение интенсивности представляет собой интер-ференционную картину, получающуюся в результате интерференции двух когерентных волн, начальная разность фаз между которыми равна нулю. В случае, если начальная разность фаз d отлична от нуля, получим смещенную относительно точек S1 и S2 картину, причем величина смещения будет зависеть от этой начальной разности фаз. Для некогерентных волн каждому значению d будет соответствовать своя интерференционная картина, которая с течением времени Физическая причина некогерентности световых волн заключена в специфике протекания атомных процессов. Излучение светящегося тела слагается из волн, испускаемых атомами вещества, из которого оно состоит. В двух самостоятельных источниках мы всегда имеем дело с излучением атомов, не связанных друг с другом. Процесс испускания отдельного атома длится очень короткое время (tисп. ~ 10-8с), после чего он обрывается вследствие потери энергии как в виде излучения, так и в результате взаимодействия с окружающими атомами. За время tисп атом успевает испустить цуг волн определенной длины. Так, при частоте света порядка 1015 Гц такой цуг содержит 10-8 1015 = 107 длин волн, т.е. монохроматичность такого цуга очень высока. После прекращения излучения атом может вновь начать испускать, однако фаза нового цуга волн не связана с фазой предыдущего цуга. Поэтому разность фаз между излучениями двух таких независимых атомов будет изменяться всякий раз при начале нового акта испускания. Таким образом, ряд физических процессов, происходящих в источнике света, определяет тот минимальный интервал времени, в течение которого фазу и амплитуду испускаемой волны можно считать постоянными. Этот промежуток времени называют временем когерентности (tког.), которое оценивается примерно 10-9-10-10с. Зная время когерентности, можно оценить другую, очень важную физическую величину - длину когерентности: Lког = сtког. (6) т.е. расстояние, на которое распространяется волна за время пока ее фаза и амплитуда остаются в среднем постоянными. Очевидно, что при принятой оценке tког. длина когерентности в оптике составляет 3-30см. В некоторых частных случаях Lког может совпадать с длиной волнового цуга, равной сtког.. D < сtког.(7) Это означает, что необходимо создать тем или иным способом две системы волн и затем свести их вместе в какой-либо точке пространства. Если при этом для разности хода выполняется условие (7), интерференция должна наблюдаться. В оптике для получения двух систем волн используют различные устройства, основанные на законах преломления и отражения. При этом можно вместо одного действительного источника получить два действительных, действительный и мнимый или два мнимых источника, от которых и рассматривается в дальнейшем интерференция. Такое различие в источниках несущественно, ибо волна, идущая от реального источника, при помощи соответствующего оптического устройства разделяется на две световые волны, интерферирующие в некоторой области. Использование мнимых изображений служит лишь удобным способом определения области перекрытия лучей, где можно наблюдать интерференцию. Существует ряд различных схем, позволяющих наблюдать явление интерференции. Рассмотрим одну из них. Кольца Ньютона
Кольца Ньютона представляют собой интерференционные полосы, возникающие при наложении волн, отраженных от верхней и нижней поверхностей тонкой воздушной прослойки, заключенной между стеклянной пластинкой и наложенной на нее линзой большого радиуса кривизны (рис.2). Рис.2 Ширина воздушного слоя увеличивается от точки соприкосновения N к краям линзы. В точках P1 и P2, равноотстоящих от точки N, толщина слоя одинакова. На всей поверхности пластины равные толщины слоя располагаются по концентрическим окружностям с центром в точке N.Если осветить систему пластинка - линза почти параллельным пучком монохроматческого света., то в отраженном свете наблюдается большое число чередующихся светлых и темных концентрических колец с темным пятном в области точки N. Эти полосы равной толщины называются кольцами Ньютона. Темное пятно в центре колец (при наблюдении в отраженном свете) объясняется тем., что геометрическая разность хода между интерферирующими волнами в области точки N практически равна нулю и лишь теряется полуволна Разность хода интерферирующих волн 1 и 2 D = 2d×n. Для воздушного слоя n = 1. Кроме указанной разности хода появляется дополнительная разность хода в полволны
Таким образом, полная разность хода между волнами 1 и 2 будет: 1). для темных колец 2). для светлых колец где m = 1,2,3… Рассчитаем радиусы колец Ньютона rm, наблюдаемых в отраженном свете. Рис.3
Из рис.3 следует, что для кольца порядка m:
Так как dm<<2R, то 2R-dm
Откуда
Подставляя в формулы (9) и (10) выражение для dm получим: 1). для темных колец 2). для светлых колец Из этих формул можно было бы определить l, зная радиус кольца, радиус кривизны линзы и порядок минимума (или максимума). Однако вследствие упругой деформации стекла невозможно добиться идеального соприкосновения линзы и пластинки в точке О. Поэтому более точно результат получится, если вычислять l по разности диаметров двух колец порядка dk и dm. Для темных колец имеем:
Откуда
Таким образом, зная радиус кривизны линзы и диаметры темных интерференционных колец:, можно по формуле (14) вычислить длину световой волны l. Экспериментальная часть Упражнение 1. Определение цены деления окулярного микрометра. При помощи объект-микрометра определить цену деления окулярной шкалы. Для этого объект-микрометр поместить на предметный столик микроскопа. Наблюдая в окуляр, добиться резкого изображения шкалы. Поворотом объект-микрометра добиться параллельности штрихов обеих шкал. Выбрать в центре поля определенное число делений шкалы объект-микрометра и по шкале окуляра определить, сколько делений шкалы окуляра занимает изображение выбранного числа делений шкалы объект-микрометра. Зная цену деления последнего (0,01мм), определить цену деления окулярной шкалы. Упражнение 2. Определение радиуса кривизны линзы.. а). Установить на предметный столик плоскопараллельную пластинку с линзой. б). Установить зеленый светофильтр (l = 546 нм). в). Осуществить фокусировку микроскопа на поверхности пластинки, прижатой к линзе, и перемещением столика микроскопа в горизонтальной плоскости обнаружить интерференционные кольца. г). Добиться расположения колец в поле зрения окуляра. д). Измерить при помощи окулярной шкалы диаметр трех колец (порядка не ниже шестого в случае использования лампы накаливания и более высоких порядков при использовании ртутной лампы). Записать результаты в заранее заготовленную таблицу. е). По известной длине волны, пользуясь уравнением (14), рассчитать радиус кривизны линзы. Рассчитать погрешность измерения. Упражнение 3. Определение длины волны пропускания светофильтра. а). Заменив зеленый светофильтр на красный, повторить измерение радиу-сов (диаметров) колец. б). Взять для R значения, полученные в упражнении 2, определить длину световой волны. в) Рассчитать погрешность измерения. Литература 1. Ландсберг Г.С. Оптика, М.,1976. 2. Савельев И.В. Курс общей физики, т. II, М., 1978. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 - волновое число,
- волновое число,

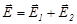
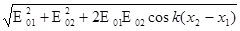
 +E
+E  E01E02cos k(x2 - x1) (2.1)D
E01E02cos k(x2 - x1) (2.1)D cos k(x2 - x1) (2.2)
cos k(x2 - x1) (2.2) (2m+1) p.
(2m+1) p. (4)
(4) D.
D. будет сменяться другой. Если такая смена происходит достаточно быстро, мы не в состоянии наблюдать эти интерференционные картины и воспринимаем некоторое среднее состояние, соответствующее равномерному распределению интенсивности.
будет сменяться другой. Если такая смена происходит достаточно быстро, мы не в состоянии наблюдать эти интерференционные картины и воспринимаем некоторое среднее состояние, соответствующее равномерному распределению интенсивности.
 (8)
(8) (9)
(9) (10)
(10)
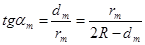
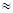 2R следовательно:
2R следовательно: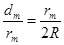
 (11)
(11) (12)
(12) (13)
(13)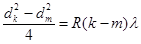
 (14)
(14)