
|
|
Лист 2 «Кинетостатическое исследование плоского рычажного механизма. Определение момента инерции маховика»
Для выполнения второго листа графической части курсового проекта необходимо проделать следующее. 1. На листе формата А1 построить 12 положений механизма в масштабе длин 2. Для расчетного положения определить реакции во всех кинематических парах механизма методом планов и уравновешивающую силу. Для этого необходимо: • вычертить отдельно структурные группы и механизм первого класса; • по индикаторной диаграмме (диаграмме усилий) определить величину движущей силы или силы производственных сопротивлений и приложить ее к соответствующему звену; для вычисления можно воспользоваться уравнением:
где рi — индикаторное давление в i-том положении, МПа; Sп — площадь поршня, м2; уi — ордината индикаторной диаграммы в i-том положении, мм;
dп — диаметр поршня, м;
• определить величины сил инерции звеньев по формуле:
где m — масса звена, кг; аS — ускорение центра масс звена,
где Ми — момент сил инерции звена, IS — момент инерции звена относительно оси, проходящей через центр масс перпендикулярно плоскости движения, e — угловое ускорение звена,
Сила инерции • привести в пояснительной записке уравнения, необходимые для определения реакций в кинематических парах и уравновешивающей силы на начальном звене; выполнить необходимые расчеты; • построить планы сил для каждой структурной группы. Последовательность силового расчета групп Ассура II класса приведена в приложении Ж. 3. Выполнить расчет уравновешивающей силы по методу Н.Е. Жуковского. Для этого вычертить в произвольном масштабе повернутый на 4. Определить мгновенный механический коэффициент полезного действия механизма (к.п.д.) для расчетного положения. При этом принять диаметр цапф (шарниров) равным 20…40 мм и коэффициент трения скольжения во вращательных и поступательных парах равным 0,1. К.п.д. подсчитывается по формуле:
или
где Рпс — мгновенная мощность сил производственных сопротивлений, Вт; Рд — мгновенная мощность движущих сил, Вт; Рт — мгновенная мощность, затрачиваемая на преодоление сил трения, Вт.
Мгновенная мощность некоторой силы
где ai — угол между направлением действия силы и скоростью точки приложения этой силы, град.
Мгновенная мощность некоторого момента
где wi — угловая скорость звена, к которому приложен момент
Мощность сил трения определяется суммой мощностей сил трения во всех кинематических парах механизма. Мощность, затрачиваемая на преодоление сил трения во вращательных кинематических парах, определяется по формуле:
где R — реакция в кинематической паре, Н; f — коэффициент трения; r — радиус цапф (шарниров); wji — относительная угловая скорость звена i относительно звена j, с-1.
Величина относительной угловой скорости wji равна сумме величин угловых скоростей звеньев i и j в случае угловых скоростей разного направления. При угловых скоростях одного направления величина относительной угловой скорости определяется вычитанием меньшей величины из большей. Мощность, затрачиваемая на преодоление сил трения в поступательной кинематической паре, определяется по формуле:
где R — реакция в поступательной кинематической паре, Н; f — коэффициент трения;
Задачей исследования движения механизма является подбор массы маховика, для того чтобы данный механизм мог осуществлять работу с заданным коэффициентом неравномерности движения d. Для расчета момента инерции маховика необходимо применить метод Виттенбауэра. Для этого необходимо проделать следующее. 1. Рассчитать для каждого положения механизма приводимый к начальному звену момент Мп от внешних сил, действующих на рабочие звенья. Приводимыми силами в проектируемых механизмах являются: в двигателе внутреннего сгорания и компрессоре — силы давления газов на поршень; в механизмах режущих аппаратов сенокосилок, кормоуборочных машин — силы резания, приложенные к ножу; в механизме сенного пресса — сила давления сенной массы на пресс. Приведенный момент сил может быть получен из равенства мгновенных мощностей приводимых сил и приведенного момента:
где
Исходя из этого, можно записать:
где
Или
Знак «плюс» или «минус» выбирают исходя из следующих соображений. Для двигателей значение Мпд считают положительным, если направления приведенной силы Для рабочих машин (компрессоры, косилки, кормоуборочные машины, сенный пресс и т.д.) если направления приводимой силы Для всех 12-ти положений механизма определить значения Мп, свести их в таблицу и построить диаграмму приведенного момента сил Мп в функции угла поворота начального звена j1. 2. Графическим интегрированием диаграммы приведенных моментов сил построить диаграмму работ движущих сил или сил сопротивлений 3. Построить диаграмму приращения кинетической энергии
Приняв 4. Рассчитать для каждого положения механизма приведенный к начальному звену момент инерции Iп. Для этого принять кинетическую энергию звена приведения равной кинетической энергии механизма (сумме кинетических энергий подвижных звеньев) и из полученного уравнения выразить Iп. Значения Iп для всех положений привести в таблице. Построить диаграмму приведенного момента инерции механизма Iп в функции угла поворота начального звена j. Ось Iп диаграммы расположить горизонтально. 5. Путем исключения общего параметра j из диаграммы изменения кинетической энергии и приведенного момента инерции построить диаграмму Виттенбауэра 6. По заданному коэффициенту неравномерности d и средней угловой скорости начального звена wср определить углы Построив стороны этих углов и перенеся их параллельно самим себе до момента касания с кривой энергомасс соответственно сверху и снизу, получить на оси По длине этого отрезка определить момент инерции маховика. Размещение диаграмм на чертеже можно выполнить по аналогии с прилагаемым листом.
Вопросы для самоконтроля по кинетостатическому исследованию механизма и расчету маховика 1. Какие задачи решаются в кинетостатическом исследовании механизма? Методика проведения исследований. 2. Какая кинематическая цепь является статически определимой? 3. Объясните назначение и построение индикаторных диаграмм (диаграмм усилий). 4. Объясните определение сил, действующих на звенья механизма: - движущих или сил производственных сопротивлений; - сил инерции; - реакций в кинематических парах механизма. 5. Как определить уравновешивающую силу методом планов и методом рычага Н.Е. Жуковского? 6. Принцип Д’Аламбера и его применение в силовом расчете. 7. Объясните последовательность проведения силового расчета групп Ассура, входящих в исследуемый механизм. 8. Что называется приведенным моментом сил и как он определяется для данного механизма? 9. Что называется приведенным моментом инерции и как он определяется для данного механизма? 10. Объясните построение диаграмм: - приведенных моментов сил; - приведенных моментов инерции; - работ; - приращений кинетической энергии; - энергомасс. 11. Что называется коэффициентом неравномерности движения? Как он учитывается при исследовании движения механизма? 12. Как определяется момент инерции маховика Iм? 13. Объясните назначение маховика и необходимость его установки в исследуемом механизме. 14. Объясните физический смысл точки пересечения касательных к диаграмме энергомасс. 15. Как по диаграмме энергомасс определить угловую скорость звена приведения для любого положения механизма? 16. Как определить кинетическую энергию заданного механизма? 17. Что называется механическим коэффициентом полезного действия? 18. Как определяется мощность движущих сил и сил производственных сопротивлений для заданного механизма? 19. Как определяются мощности, затрачиваемые на преодоление сил трения в кинематических парах?
3.3 Лист 3 «Проектирование кулачкового и планетарного Зубчатого механизмов»
В объем данного листа входит решение следующих задач: 1) динамическое проектирование кулачкового механизма наименьших размеров, удовлетворяющего заданным условиям. Задачей синтеза кулачкового механизма является определение основных его размеров и геометрии профиля кулачка, обеспечивающих воспроизведение требуемого закона движения толкателя. 2) геометрическое проектирование эвольвентного зацепления пары цилиндрических прямозубых колес: - расчет геометрических размеров зубчатой передачи; - определение коэффициентов перекрытия и удельных скольжений; - оценка проектируемой передачи по геометрическим показателям; 3) проектирование зубчатого механизма с планетарной ступенью по заданному значению передаточного отношения: - подбор числа зубьев колес механизма (для планетарной ступени проверить выполнение условия соосности валов); - аналитическое и графическое кинематическое исследование спроектированного механизма. Для решения поставленных задач необходимо выполнить следующее. 1. В соответствии с заданным законом движения ведомого звена кулачкового механизма построить диаграммы аналога ускорения толкателя (коромысла) в функции угла поворота кулачка (приложения П, Р). Примечание. В приложении Г представлены графические изображения законов движения толкателя (коромысла) кулачкового механизма в интервале углов удаления и возвращения. Рекомендуется использовать известные методы построения кривых (синусоиды, косинусоиды и др.). 2. Методом графического интегрирования (приложение К) построить диаграммы аналога скорости и перемещения толкателя (коромысла) в функции угла поворота кулачка. 3. Вычислить масштабы диаграмм движения толкателя (коромысла). 4. Определить графически минимальный радиус кулачка, а также величину смещения для кулачкового механизма со смещенным поступательно движущимся толкателем или величину межосевого расстояния для коромыслового кулачкового механизма. 5. Построить центровой (теоретический) профиль кулачка. Определить радиус ролика и построить действительный профиль кулачка. 6. Рассчитать параметры зубчатых колес для построения картины зацепления. 7. Вычертить картину зацепления пары цилиндрических прямозубых колес (приложения Л, П, Р). При этом необходимо соблюдать следующие условия: - стандартный масштаб построения должен быть таким, чтобы полная высота зуба изображалась отрезком не менее 45 мм (центры колес могут находиться вне чертежа); - на каждом из колес должны быть вычерчены по три зуба, причем один из профилей зуба каждого колеса необходимо вычертить по правилам построения эвольвенты, а остальные — при помощи шаблонов. Все вспомогательные линии построения должны быть видны на чертеже. При выполнении картины зацепления нулевых колес необходимо, чтобы выполнялось условие:
где
8. Построить дуги зацепления на обоих колесах, активные профили зубьев и диаграммы коэффициентов удельного скольжения профилей. 9. Вычислить коэффициенты удельного скольжения профилей зубьев. Определить коэффициент перекрытия зубчатой передачи графически и аналитически. 10. Подобрать числа зубьев колес зубчатого механизма для заданного передаточного отношения. Для планетарной ступени числа зубьев колес подбирать исходя из условия соосности валов. 11. Произвести кинематическое исследование спроектированного зубчатого механизма аналитическим и графическим методами. 12. Обосновать преимущества и недостатки механизмов с высшими кинематическими парами. Сделать краткие выводы о работе механизмов.
Вопросы для самоконтроля по проектированию кулачкового и планетарного зубчатого механизмов
1. Типы кулачковых механизмов. Преимущества и недостатки кулачковых механизмов в сравнении с рычажными. 2. Виды замыканий высшей пары. 3. Основные законы движения выходного звена кулачкового механизма. При каких законах движения наблюдаются удары и какие законы движения желательно применять в быстроходных кулачковых механизмах? 4. Объясните построение кинематических диаграмм выходного звена. 5. Как определяются масштабные коэффициенты диаграмм? 6. Угол давления и угол передачи движения в кулачковом механизме и их связь с основными размерами кулачкового механизма. 7. Как определить минимальный радиус кулачка по заданному закону движения толкателя и углу давления для плоского кулачкового механизма с поступательно движущимся толкателем или с коромыслом? 8. В чем заключается сущность метода «обращенного движения»? 9. Как определяются основные размеры плоского кулачкового механизма? 10. Сформулируйте и докажите основную теорему зацепления. 11. Какому условию должны удовлетворять профили зубьев передачи с постоянным передаточным отношением? 12. Что называется эвольвентой? Каковы ее основные свойства? Что называется углом профиля эвольвенты? 13. Охарактеризуйте основные методы изготовления эвольвентных зубчатых колес. Что такое исходный производящий контур и каковы его основные параметры? 14. Что такое окружной модуль зубьев, расчетный модуль зубчатого колеса, делительная окружность? 15. Что называется шагом зацепления? Как определить шаг по делительной и основной окружностям, их диаметры? 16. Охарактеризуйте основные характеристики эвольвентного зацепления: полюса зацепления, линии зацепления, угла зацепления, активной линии зацепления, активных профилей зубьев, дуги зацепления и коэффициента перекрытия. Какие окружности зубчатой передачи называются начальными? 17. По каким формулам определяются основные размеры цилиндрических эвольвентных колес: толщина зуба по делительной и основной окружности, радиусы окружностей вершин и впадин зубьев? 18. Что называется начальным межосевым расстоянием, делительным межосевым расстоянием? 19. Почему дуга зацепления должна быть больше шага зацепления? 20. Какой механизм называется планетарным? 21. Как определить передаточное отношение последовательно соединенных ступеней зубчатых колес? 22. В чем состоит сущность «обращенного движения» для планетарных механизмов? 23. Как получена формула Виллиса для планетарных механизмов? 24. Как аналитически и графически определить передаточное отношение планетарного механизма?
ПРИМЕР 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (приложение О). Расчетное положение (см. задание) обвести основными линиями. Вычертить индикаторную диаграмму (диаграмму усилий), произвести ее разметку в соответствии с ходом рабочих звеньев. Рекомендуется размещать ось S индикаторной диаграммы (диаграммы усилий) параллельно оси движения рабочего звена (приложение В).
(приложение О). Расчетное положение (см. задание) обвести основными линиями. Вычертить индикаторную диаграмму (диаграмму усилий), произвести ее разметку в соответствии с ходом рабочих звеньев. Рекомендуется размещать ось S индикаторной диаграммы (диаграммы усилий) параллельно оси движения рабочего звена (приложение В). (3.3)
(3.3) — сила производственных сопротивлений (движущая сила), Н;
— сила производственных сопротивлений (движущая сила), Н; — масштабный коэффициент индикаторной диаграммы по оси р,
— масштабный коэффициент индикаторной диаграммы по оси р, 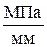 ;
; (3.4)
(3.4) .
. (3.5)
(3.5) ;
; ;
; .
. прикладывается в центре масс звена и направляется противоположно направлению ускорения центра масс
прикладывается в центре масс звена и направляется противоположно направлению ускорения центра масс  , момент сил инерции
, момент сил инерции  направляется в сторону, противоположную угловому ускорению звена e;
направляется в сторону, противоположную угловому ускорению звена e; план скоростей, в соответствующих точках которого приложить все внешние силы (силы производственных сопротивлений), силы тяжести и силы инерции, соблюдая их направления. Затем из уравнения моментов сил относительно полюса плана скоростей р определить уравновешивающую силу. Расхождение значений уравновешивающей силы, полученных методом планов сил и методом Н.Е. Жуковского, должно находиться в пределах 8 %.
план скоростей, в соответствующих точках которого приложить все внешние силы (силы производственных сопротивлений), силы тяжести и силы инерции, соблюдая их направления. Затем из уравнения моментов сил относительно полюса плана скоростей р определить уравновешивающую силу. Расхождение значений уравновешивающей силы, полученных методом планов сил и методом Н.Е. Жуковского, должно находиться в пределах 8 %. (3.6)
(3.6) (3.6а)
(3.6а) определяется по формуле:
определяется по формуле: (3.7)
(3.7) — скорость точки приложения силы
— скорость точки приложения силы 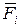 ,
,  ;
; определяется как
определяется как (3.8)
(3.8) (3.9)
(3.9) (3.10)
(3.10)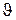 — скорость поступательной пары,
— скорость поступательной пары,  (3.11)
(3.11) — мгновенная мощность, развиваемая приведенным моментом, Вт;
— мгновенная мощность, развиваемая приведенным моментом, Вт; — мгновенная мощность, развиваемая приводимой силой Fi, Вт.
— мгновенная мощность, развиваемая приводимой силой Fi, Вт. (3.12)
(3.12) — угловая скорость звена приведения, с-1;
— угловая скорость звена приведения, с-1; ,
,  — угол, образованный силой
— угол, образованный силой  и вектором скорости
и вектором скорости  , град.
, град. (3.13)
(3.13) . Соединив прямой линией начало и конец кривой диаграммы работ, построенной графическим интегрированием, получим диаграмму сил сопротивлений или движущих сил. При этом приведенный момент сил сопротивлений (движущих сил) принимается постоянным и действующим в течение всего цикла установившегося движения. Продифференцировав полученную прямую, на диаграмме приведенных моментов сил получим горизонтальную прямую, определяющую величину постоянного приведенного момента сил сопротивления (движущих сил).
. Соединив прямой линией начало и конец кривой диаграммы работ, построенной графическим интегрированием, получим диаграмму сил сопротивлений или движущих сил. При этом приведенный момент сил сопротивлений (движущих сил) принимается постоянным и действующим в течение всего цикла установившегося движения. Продифференцировав полученную прямую, на диаграмме приведенных моментов сил получим горизонтальную прямую, определяющую величину постоянного приведенного момента сил сопротивления (движущих сил).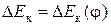 , исходя из уравнения:
, исходя из уравнения: (3.14)
(3.14) , эту диаграмму можно построить, вычитая из ординат диаграммы работ движущих сил ординаты диаграммы работ сил сопротивлений.
, эту диаграмму можно построить, вычитая из ординат диаграммы работ движущих сил ординаты диаграммы работ сил сопротивлений. (изменение кинетической энергии в функции приведенного момента инерции механизма).
(изменение кинетической энергии в функции приведенного момента инерции механизма). и
и  , образуемые касательными к диаграмме энергомасс с осью абсцисс.
, образуемые касательными к диаграмме энергомасс с осью абсцисс. отрезок, заключенный между этими касательными.
отрезок, заключенный между этими касательными. (3.15)
(3.15) — толщина зуба по начальной окружности соответственно первого и второго колеса;
— толщина зуба по начальной окружности соответственно первого и второго колеса; — ширина впадины по начальной окружности соответственно первого и второго колеса.
— ширина впадины по начальной окружности соответственно первого и второго колеса.