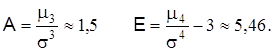|
|
Начальные и центральные моментыЛЕКЦИЯ 7 Числовые характеристики случайных величин. Математическое ожидание, дисперсия, среднее квадратичное отклонение, начальные и центральные моменты, мода и медиана. 5. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ Функция распределения полностью характеризует случайную величину. Действительно, функция распределения одновременно указывает на то, какие значения может принимать случайная величина и с какими вероятностями. С точки зрения наблюдателя, две случайные величины, имеющие одинаковые функции распределения, неразличимы, несмотря на то что они могут быть заданы на разных вероятностных пространствах и описывать разные явления. Так, например, при игре в "орлянку" все равно, какая монета бросается. Однако составить полное представление о случайной величине только по функции распределения бывает часто довольно трудно. Еще труднее сравнивать случайные величины. В связи с этим вводят более простые характеристики случайной величины, определяемые только одним числом. Хотя числовые характеристики не дают полного представления о случайной величине, однако они в сжатой форме выражают наиболее важные черты распределения. Числовые характеристики играют большую роль в теории вероятностей и ее приложениях. Основную роль на практике играют – математическое ожидание, характеризующее "центральное" значение случайной величины, и дисперсия, характеризующая "разброс" вокруг математического ожидания. Среди остальных характеристик можно выделить те, которые применяются в специальных вероятностных дисциплинах (например, квантили широко используются в математической статистике), и те, которые носят ярко выраженный теоретический характер (например, моменты высших порядков). Математическое ожидание Одной из важнейших и, в тоже время, наиболее простой характеристикой случайной величины является математическое ожидание. Введение математического ожидания тесно связано с понятием среднего арифметического значения, используемого в математической статистике. В связи с этим вместо термина "математическое ожидание" используется термин "среднее значение". Отметим также, что математическое ожидание имеет аналог и в теоретической механике. Если считать возможные значения случайной величины xi, координатами неких точек, то математическое ожидание будет характеризовать центр тяжести такой системы точек. В связи с этим, математическое ожидание иногда называют центром распределения. Математическое ожидание будем обозначать буквой M (отметим, что в зарубежной литературе для этого часто используется буква E, от англ. expectation – ожидание). Если нужно указать для какой случайной величины вычисляется математическое ожидание, то будем писать M[X], M(X) или Mx. Математическим ожиданием ДСВ X называется сумма произведений ее возможных значений на их вероятности: M[X] = Если ДСВ X принимает бесконечное число значений, то M[X] = при условии, что этот ряд сходится абсолютно, т.е. сходится ряд:
В противном случае говорят, что математическое ожидание случайной величины X не существует. Пример 5.1. Найти математическое ожидание случайных величин: X={xn=n} и Y={yn=(–1)n}, где n=1,2,..., если вероятности определяются по формуле
Решение. Непосредственно проверяется, что
Находим математическое ожидание случайной величины X: M[X] = Поскольку полученный ряд расходится, то M[X] не существует. Далее вычисляем математическое ожидание случайной величины Y: M[Y] = Используя разложение ln(1+x)= M[Y] = 1–2ln2. Для определения математического ожидания НСВ X, имеющей плотность распределения f(x), заметим, допуская некоторую вольность изложения, что случайная величина X принимает значение x с вероятностью f(x)dx. Заменив сумму на интеграл, получим, что: Математическим ожиданием НСВ X с плотностью распределения f(x) называется интеграл: M[X] = Здесь предполагается, что несобственный интеграл сходится абсолютно, т.е. существует интеграл
В противном случае говорят, что математическое ожидание случайной величины X не существует. Пример 5.2. НСВ X задана плотностью распределения:
Найти математическое ожидание случайной величины X. Решение. Поскольку f(x) при x<0 и x>0, то
Пример 5.3. НСВ X задана плотностью распределения Коши:
Найти M[X]. Решение. Распределение Коши удовлетворяет всем свойствам функции распределения, в частности:
Однако
т.е. математическое ожидание случайной величины X не существует.
В общем случае математическое ожидание случайной величины произвольной природы задается выражением
где интеграл понимается в так называемом смысле Стилтьеса. Поскольку мы рассматриваем только дискретные и непрерывные случайные величины, то выражение (5.3) трактовать как обобщенную запись формул для математических ожиданий ДСВ и НСВ. Отметим некоторые свойства математического ожидания. Свойство 1. Математическое ожидание постоянной величины равно этой величине: M[C] = C. Действительно, постоянную С можно рассматривать как ДСВ, которая может принимать только одно значение C с вероятностью 1; поэтому M[C]=C×1=C. Свойство 2. Постоянный множитель можно выносить за знак математического ожидания: M[CX] = C M[X] Свойство 3. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий: M[X+Y] = M[X] + M[Y]. Свойства 2 и 3 следуют из соответствующих свойств интеграла или ряда. Здесь только отметим, что под суммой двух случайных величин X и Y понимается случайная величина X+Y, возможные значения которой равны суммам каждого возможного значения X с каждым возможным значением Y; вероятности возможных значений X+Y для независимых величин X и Y равны произведениям вероятностей слагаемых, для зависимых величин – произведениям вероятности одного слагаемого на условную вероятность другого (см. теорему об умножении вероятностей). Свойство 4. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: M[XY] = M[X]×M[Y]. Свойство 4 также следует из соответствующих свойств интеграла или ряда. Здесь только отметим, что под произведением двух независимых случайных величин X и Y понимается случайная величина XY, возможные значения которой равны произведениям каждого возможного значения X с каждым возможным значением Y; вероятности возможных значений XY равны произведениям вероятностей возможных значений сомножителей. Разность X–M[X] называется отклонением случайной величины X от ее математического ожидания. Эта разность также есть случайная величина. Свойство 5. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю: M[X–M[X]] = 0. Действительно, используя свойства математического ожидания и принимая во внимание, что M[X] – постоянная величина, получим M[X–M[X]] = M[X]– M[M[X]] = M[X]– M[X] = 0. Дисперсия В большинстве случаев математическое ожидание еще не достаточно характеризует случайную величину. На практике встречаются случайные величины, имеющие одинаковые математические ожидания, однако принимающие резко различающиеся значения. У одних из этих величин отклонения значений от математического ожидания небольшие, а для других, наоборот, значительны, т.е. для одних рассеивание значений случайной величины вокруг математического ожидания мало, а для других оно велико. Например, пусть случайные величины X и Y заданы следующими законами распределения:
Математические ожидания этих случайных величин одинаковы и равны нулю. Однако характер их распределения их различный. Случайная величина X принимает значения, мало отличающиеся от математического ожидания, а случайная величина Y – значения, значительно отличаются от математического ожидания. Приведенные рассуждения и пример свидетельствую о целесообразности введения такой характеристики случайной величины, которая оценивала бы меру рассеивания значений случайной величины вокруг ее математического ожидания, тем более что на практике часто приходится оценивать такое рассеивание. Например, артиллеристам необходимо знать как кучно лягут снаряды вблизи цели, по которой ведется стрельба. На первый взгляд может показаться, что для оценки рассеяния проще всего вычислить все возможные значения отклонения случайной величины и затем найти их среднее значение. Однако такой путь ничего не дает, т.к. среднее значение отклонение для любой случайной величины равно нулю. Это объясняется тем, что возможные значения X–M[X] могут иметь как положительные, так и отрицательные знаки. Избежать изменения знаков отклонений xi– M[X] можно, если заменить их абсолютными значениями или возвести в квадрат. Замена отклонений их абсолютными величинами нецелесообразно, т.к. действия с абсолютными величинами, как правило, вызывают затруднения. Поэтому следует использовать величину (X–M[X])2 (точнее, ее среднее значение) для характеристики рассеивания значений случайной величины. Определение. Дисперсией (рассеянием) случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
Законы распределения вероятностей случайной величины X и (X–M[X])2 одинаковы. Пусть M[X]ºm, тогда дисперсия ДСВ будет иметь вид
дисперсия НСВ дисперсия Из определения следует, что дисперсия случайной величины есть величина не случайная (постоянная). Тогда формулу для дисперсии можно преобразовать следующим образом
Таким образом,
Это есть основная формула для вычисления дисперсии. Случайная величина и ее математическое ожидание имеют одну и ту же размерность, но дисперсия имеет размерность квадрата случайной величины. недостатка можно избежать если воспользоваться величиной, равной квадратному корню из дисперсии:
Эта случайная величина называется средним квадратичным отклонением случайной величиной. Пример 5.4. ДСВ X задана следующим законом распределения:
Найти дисперсию D[X] двумя способами и среднее квадратичное отклонение. Решение. Способ 1.
Способ 2.
Среднее квадратичное отклонение
Пример 5.5. НСВ X задана следующей плотностью распределения:
Найти дисперсию D[X] двумя способами и среднее квадратичное отклонение. Решение. Способ 1.
Способ 2.
Среднее квадратичное отклонение
Отметим некоторые свойства дисперсии. Свойство 1. Дисперсия постоянной величины равно нулю: D[C] = 0. Действительно, т.к. M[С]=C, то D[C]=M[С–M(С)]2=M[С–С]2=M[0]=0. Это свойство очевидно, т.к. постоянная величина принимает только одно значение, следовательно, рассеяние рассеяния вокруг математического ожидания нет. Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D[CX] = C2 D[X]. Действительно, т.к. постоянный множитель можно выносить за знак математического ожидания, то
Свойство 3. Дисперсия суммы двух независимых случайных величин равно сумме дисперсий этих величин: D[X+Y] = D[X]+ D[Y]. Действительно, учитывая свойства математического ожидания, получим
Свойство 4. Дисперсия разности двух независимых случайных величин равно сумме их дисперсий: D[X–Y] = D[X] + D[Y]. Действительно, в силу свойства 3 D[X–Y] = D[X] + D[–Y]. В соответствие со свойством 2, получим
Ранее было введено понятие отклонения случайной величины от ее математического ожидания. Эту случайную величину X–M[X] Иногда называют центрированной случайной величиной. Выше было показано (свойство 5), что математическое ожидание случайной величины равно нулю. Найдем дисперсию центрированной случайной величины. На основании свойств дисперсии, получим
Таким образом, дисперсия случайной величины X и центрированной случайной величины X–M[X] равны между собой. Иногда бывает удобно использовать безразмерные центрированные случайные величины. Разделим величину X–M[X] на среднее квадратичное отклонение s имеющее ту же размерность. Вновь полученную случайную величину называют стандартной случайной величиной:
Стандартная случайная величина обладает следующими свойствами: 1) M[Z]=0, 2) D[X]=1. Начальные и центральные моменты Начальным моментом k-го порядка случайной величины X называется математическое ожидание величины Xk:
В частности,
Центральным моментом k-го порядка случайной величины X называется математическое ожидание величины [X–M(X)]k:
В частности,
Воспользовавшись определениями и свойствами математического ожидания и дисперсии, можно получить, что
Моменты более высоких порядков применяются редко. Предположим, что распределение случайной величины симметрично относительно математического ожидания. Тогда все центральные нечетного порядка равны нулю. Это можно объяснить тем, что для каждого положительного значения отклонения X–M[X] найдется (в силу симметричности распределения) равное ему по абсолютной величине отрицательное значение, причем их вероятности будут одинаковыми. Если центральный момент равен нечетного порядка не равен нулю, то это говорит об асимметричности распределения и чем больше момент, тем больше асимметрия. Поэтому в качестве характеристики асимметрии распределения разумнее всего взять какой-нибудь нечетный центральный момент. Так как центральный момент 1-го порядка всегда равен нулю, то целесообразно для этой цели использовать центральный момент 3-го порядка. Однако принять этот момент для оценки асимметричности неудобно потому, что его величина зависит от единиц, в которых измеряется случайная величина. Чтобы устранить этот недостаток, m3 делят на s3 и таким образом получают характеристику. Коэффициентом асимметрии A называется величина
Как известно, дисперсия (2-й центральный момент) служит для характеристики рассеивания значений случайной величины вокруг математического ожидания. Чем больше дисперсия, тем более полога соответствующая кривая распределения. Однако нормированный момент 2-го порядка m2/s2 не может служить характеристикой "плосковершинности" или "островершинности" распределения потому, что для любого распределения D[x]/s2=1. В этом случае используют центральный момент 4-го порядка. Эксцессом E называется величина
Пример 5.6. ДСВ X задана следующим законом распределения:
Найти коэффициент асимметрии и эксцесс.
Теперь вычислим центральные моменты:
Таким образом,
Пример 5.7. НСВ X задана следующей плотностью распределения:
Найти коэффициент асимметрии и эксцесс.
Теперь вычислим центральные моменты:
Таким образом,

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 = x1p1+x2p2+ ... +xnpn. (5.1)
= x1p1+x2p2+ ... +xnpn. (5.1) ,
, .
. .
. .
. .
.
 .
.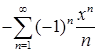 при x=1, получим
при x=1, получим . (5.2)
. (5.2) .
.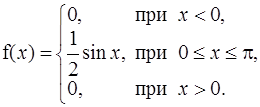
 .
. .
. .
. ,
, , (5.3)
, (5.3) . (5.4)
. (5.4) , (5.5)
, (5.5)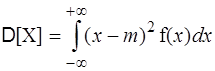 . (5.6)
. (5.6)
 . (5.7)
. (5.7) . (5.8)
. (5.8)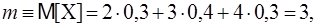
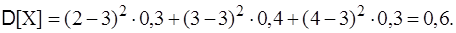
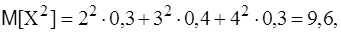
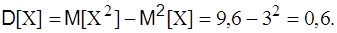
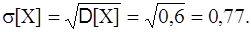
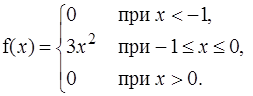
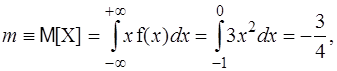
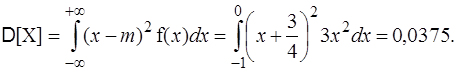
 ,
,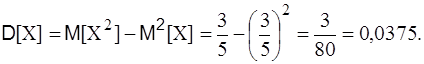
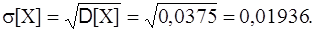
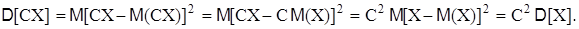
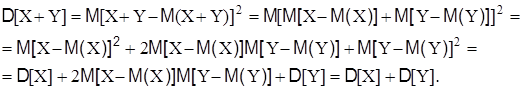
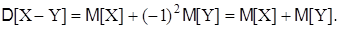
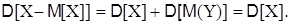
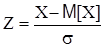 . (5.9)
. (5.9) . (5.10)
. (5.10)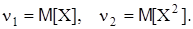
 . (5.11)
. (5.11)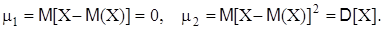
 ,
, ,
, .
. . (5.12)
. (5.12) Если коэффициент асимметрии отрицателен, то это говорит о большом влиянии на величину m3 отрицательных отклонений. В этом случае кривые распределения более пологи слева от M[X]. Если коэффициент A положителен, то кривая более пологи справа.
Если коэффициент асимметрии отрицателен, то это говорит о большом влиянии на величину m3 отрицательных отклонений. В этом случае кривые распределения более пологи слева от M[X]. Если коэффициент A положителен, то кривая более пологи справа. . (5.13)
. (5.13) Число 3 здесь выбрано потому, что для наиболее распространенного нормального закона распределения m4/s4=3. Поэтому эксцесс служит для сравнения имеющихся распределений с нормальным, у которого эксцесс равен нулю. Это означает, что если у распределения эксцесс положителен, то соответствующая кривая распределения более "островершина" по сравнению с кривой нормального распределения; если у распределения эксцесс отрицателен, то соответствующая кривая более "плосковершина".
Число 3 здесь выбрано потому, что для наиболее распространенного нормального закона распределения m4/s4=3. Поэтому эксцесс служит для сравнения имеющихся распределений с нормальным, у которого эксцесс равен нулю. Это означает, что если у распределения эксцесс положителен, то соответствующая кривая распределения более "островершина" по сравнению с кривой нормального распределения; если у распределения эксцесс отрицателен, то соответствующая кривая более "плосковершина". Решение. Предварительно найдем начальные моменты до 4-го порядка
Решение. Предварительно найдем начальные моменты до 4-го порядка
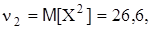

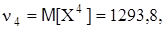
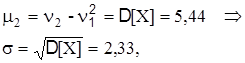

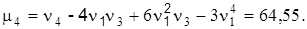
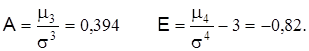
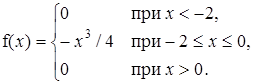
 Решение. Предварительно найдем начальные моменты до 4-го порядка
Решение. Предварительно найдем начальные моменты до 4-го порядка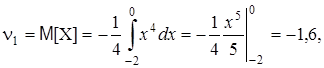
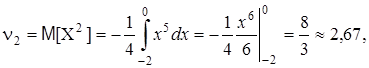
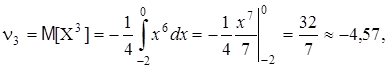
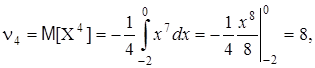
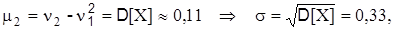

 .
.