
|
|
Закон распределения дискретной случайной величины12 Пусть X – ДСВ, принимающая в результате испытаний следующие возможные значения: x1, x2, ..., xn. Появление тех или иных значений случайной величины можно рассматривать как случайные события, которым, в общем случае, соответствуют различные вероятности. Обозначим вероятности этих событий через p с соответствующими индексами: P(X=x1)=p1, P(X=x2)=p2, ..., P(X=xn)=pn. Поскольку в результате испытания случайная величина X примет одно и только одно из перечисленных значений, т.е. произойдет одно из совместных событий, образующих полную группу, то сумма вероятностей всех возможных значений случайной величины X равна единице:
Если же множество значений ДСВ образует бесконечное множество, то ряд Соотношение, устанавливающее связь между возможными значениями ДСВ и вероятностями этих значений, называют законом распределения ДСВ. Закон распределения можно задать так же, как и функцию одной переменной в математическом анализе, используя табличный, графический и аналитический способы задания. Таблица, содержащая возможные значения ДСВ и соответствующие вероятности, является простейшей и наиболее распространенной формой задания закона распределения ДСВ и часто называется рядом распределения:
При графическом изображении закона распределения по оси абсцисс откладываю возможные значения случайной величины, а по оси ординат – вероятности этих значений. Соединив точки (xi,pi) отрезками, получим ломаную линию, которая называется многоугольником распределения. Аналитический способ задания закона распределения ДСВ применяется довольно редко. Пример 4.1. Монета брошена 3 раза. Случайная величина X – число появлений "орла". Составить ряд распределения, построить многоугольник распределения и найти функцию распределения случайной величины X. Решение. Вероятность появления герба в каждом испытании равна p=1/2, а противоположного события – q=1/2. Возможные значения случайной величины X: x0=0, x1=1, x2=2, x3=3. По формуле Бернулли найдем вероятности этих возможных значений:
Таким образом, закон распределения случайной величины X можно записать в виде следующего ряда распределения:
Проверка:  . Многоугольник распределения имеет вид: . Многоугольник распределения имеет вид:
Определим теперь, как выглядит функция распределения. Если задан закон распределения ДСВ, то функция распределения будет иметь вид
Действительно, пусть аргумент x принял значение xi < x £ xi+1. Тогда левее числа x на числовой оси окажутся только те значения случайной величины, которые имеют индекс 1,2, ..., i. Поэтому событие X<x наступит, если произойдет любое, неважно какое, из событий X=x1, X=x2, ..., X=xi. Так как эти события несовместны, то по теоремы сложения вероятностей получим P(X<x) = P(X=x1) + P(X=x2) + ... + P(X=xi) = Построим теперь функцию распределения для рассматриваемого примера. Если x£0, то левее этого значения нет ни одного возможного значения случайной величины X. Следовательно, F(x)=0. Если 0<x£1, то левее этого значения есть одно возможное значение случайной величины: X=0. Следовательно, F(x)=P(X=0)= =p0=1/8. Если 1<x£2, то F(x)=p0+p1=1/8+3/8=1/2. Если 2<x£3, то F(x)=p0+p1+p2=1/8+3/8+3/8=7/8. Если x>3, то F(x)=1. График функции F(x) будет иметь вид 4.4. Плотность распределения непрерывной Дискретная случайная величина может быть задана перечнем всех ее возможных значений и их вероятностей, т.е. законом распределения. Однако такой способ неприменим для непрерывных случайных величин. Это связано с тем, что вероятность любого отдельного значения НСВ равна нулю. Действительно, воспользуемся свойством 2 функции распределения и устремим a к b. В результате получим
Так как НСВ имеет непрерывную функцию распределения, то
Таким образом, в случае НСВ P(X=a)=0. На первый взгляд, этот результат кажется парадоксальным, т.к. события, вероятности которых равны нулю, рассматриваются как невозможные. В действительности это означает, что вероятность того, что НСВ примет какое-либо конкретное значение, является бесконечно малой величиной. Таким образом, нет смысла рассматривать вероятность принятия НСВ отдельного значения, а имеет смысл рассматривать вероятность попадания ее значений в какой-либо интервал. Пусть имеется НСВ X с функцией распределения F(x), относительно которой будем предполагать, что она непрерывна и дифференцируема в некотором интервале. Рассмотрим вероятность попадания значения случайной величины в интервал (x, x+Dx). Эту вероятность несложно вычислить, используя свойство 2 для функции F(x): P(x<X<x+Dx) = F(x+Dx)–F(x), т.е. равна приращению функции F(x) на этом интервале. Определим теперь вероятность, которая приходится на единицу длины рассматриваемого интервала. Для этого разделим обе части последнего равенства на длину интервала Dx. В результате получим
Перейдем в полученном равенстве к пределу при Dx®0. В результате получим производную функции F(x), которая существует, поскольку предполагалось, что F(x) – дифференцируема:
Полученная функция называется плотностью распределения: f(x) = F¢(x) (4.2) В некотором смысле плотность распределения f(x) "более удобная", чем функция F(x), поскольку позволяет в явной форме судить о характере распределения вероятностей случайной величины в небольшой окрестности той или иной точки числовой оси. Рассмотрим общие свойства плотности распределения. Свойство 1. Плотность распределения f(x) есть неотрицательная функция: f(x) ³ 0. Это свойство непосредственно вытекает из определения функции f(x) как производной неубывающей функции F(x). Из математического анализа известно, что производная неубывающей функции неотрицательна, т.е. F¢(x)³0. Свойство 2. Вероятность того, что НСВ X примет значение, принадлежащее интервалу (a,b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b:
Используя соотношение P(a£X<b)=F(b)–F(a) и формулу Ньютона-Лейбница
получаем
Так как для НСВ P(a£X<b)= P(a<X<b), получаем исходное равенство. Здесь учтено, что P(X=a)=0. Свойство 3. Несобственный интеграл от плотности распределения в пределах –¥ до +¥ равен единице:
Согласно определению несобственного интеграла и свойству 4 для функции F(x), получим
Свойство 4. Зная плотность распределения f(x), можно найти функцию распределения F(x):
Действительно,
В связи с последним свойством, функцию распределения F(x) НСВ называют интегральной функцией распределения, а плотность распределения f(x) – дифференциальной функцией распределения. Пример 4.2. Функция распределения НСВ имеет вид
Определить плотность распределения f(x) и параметр a. Найти также вероятность попадания случайной величины в интервал (0;p/2). Построить графики F(x) и f(x). Решение. Согласно определению плотности распределения: f(x)=F¢(x), получим
Для определения параметра a воспользуемся свойством 3 для f(x):
Отсюда находим, что a=1/2. Для нахождения вероятности попадания случайной величины в интервал (0;p/2) воспользуемся свойством 2 для функции F(x):
 . .
Графики F(x) и f(x) изображены ниже на рис.4.4 Пример 4.3. Случайная величина задана плотностью распределения:
Найти функцию распределения F(x), а также вероятность попадания НСВ в интервал (1;2). Решение. Воспользуемся свойством 4 для f(x):
Таким образом, искомая функция распределения F(x) имеет вид
Для нахождения вероятности попадания случайной величины в интервал (1;2) воспользуемся свойством 2 для f(x):

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. сходится к единице. Определив все возможные значения случайной величины X и правило, по которому каждому событию X=xi ставится в соответствие вероятность pi, можно получить полное представление о случайной величине.
сходится к единице. Определив все возможные значения случайной величины X и правило, по которому каждому событию X=xi ставится в соответствие вероятность pi, можно получить полное представление о случайной величине.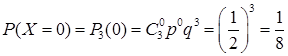 ,
, ,
, ,
, .
.
 .
. .
.
 .
.
 .
. .
. .
. .
.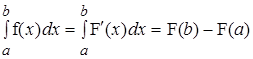 ,
, .
.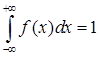 .
.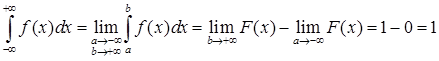 .
. .
. .
.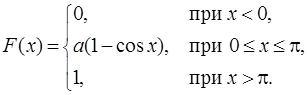
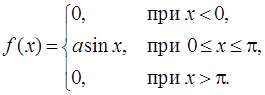
 .
.

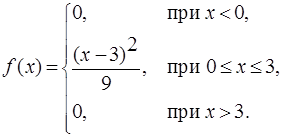
 .
.
 .
.