
|
|
Классическое определение вероятности12 ЛЕКЦИЯ 1 Предмет теории вероятностей. Случайные события и их классификация. Классическое определение вероятности. Общие принципы комбинаторики. Вероятность относится к числу таких понятий, которыми мы охотно пользуемся в повседневной жизни, совсем не задумываясь об этом. Например, даже наша речь носит отпечаток стихийно-вероятностного подхода к окружающей нас действительности. Мы часто употребляем слова "вероятно", "маловероятно", "невероятно". Уже в этих словах имеется попытка оценить возможность появления того или иного события, т.е. попытка дать количественную оценку этой возможности. Идея выражать числами степень возможности появления тех или иных событий возникла после того, как люди попытались обобщить достаточно большое число наблюдений за явлениями, в которых проявляется свойство устойчивости, т.е. способность повторяться довольно часто. Например, нельзя заранее определить результат одного подбрасывания монеты. Но если подбрасывать монету достаточно большое число раз, то почти наверняка можно утверждать, что примерно половину раз она упадет на "орла", а половину на "решку". Число подобных примеров, в которых интуитивное представление о численном значении вероятности того или иного события, можно привести очень много. Однако все подобные примеры сопровождаются неопределенными понятиями типа "честное" подбрасывание, "правильная" монета и т.п. Теория вероятностей стала наукой лишь тогда, когда были выявлены основные понятия теории вероятностей, четко сформулировано само понятие вероятности, построена вероятностная аксиоматическая модель. Любая наука, развивающая общую теорию какого-либо круга явлений, содержит ряд основных понятий, на которых она базируется. Таковы, например, в геометрии понятия точки, прямой, плоскости, линии, поверхности; в математическом анализе – функции, предела, дифференциала, интеграла; в механике – силы, массы, скорости, ускорения. Естественно, что такие понятия есть и в теории вероятностей. Одним из таких основных понятий является понятие случайного события.
СЛУЧАЙНЫЕ СОБЫТИЯ И ИХ ВЕРОЯТНОСТИ Случайные события и их классификация Под событием будем понимать любое явление, которое происходит в результате осуществления определенного комплекса условий. Осуществление этого комплекса условий называют экспериментом (опытом, испытанием). Заметим, что в проведении опыта необязательно должен участвовать сам исследователь. Опыт можно поставить мысленно, или он может протекать независимо от него; в последнем случае исследователь выступает в качестве наблюдателя. Событие называется достоверным, если оно непременно должно произойти при выполнении определенных условий. Так, достоверным является выпадение не более шести очков при бросании обычной игральной кости; утверждение, что вода является находится в жидком состоянии при +200С в нормальных условиях, и т.п. Событие называется невозможным, если оно заведомо не наступит при выполнении определенных условий. Так, невозможным событием является утверждение, что можно извлечь более четырех тузов из обычной колоды карт; или утверждение Мюнхгаузена, что он мог поднять себя за волосы, и т.п. Событие называется случайным, если оно может либо произойти, либо не произойти при выполнении определенных условий. Например, выпадение «орла» при бросании монеты; попадание в цель при одном выстреле по мишени и т.п. В теории вероятностей любое событие рассматривается как результат некоторого эксперимента. Поэтому события часто называют исходами. При этом исход того или иного эксперимента должен зависеть от ряда случайных факторов, т.е. любой исход должен являться случайным событием; в противном случае, такими событиями должны заниматься другие науки. Особо следует отметить, что в теории вероятностей рассматриваются только такие эксперименты, которые можно повторить (воспроизвести) при неизменном комплексе условий произвольное число раз (по крайней мере теоретически). То есть, теория вероятностей изучает лишь такие события, в отношении которых имеет смысл не только утверждение об их случайности, но и возможна объективная оценка доли случаев их появления. В связи с этим, подчеркнем, что теория вероятностей не занимается изучением уникальных событий, как бы они ни были интересными сами по себе. Например, утверждение, что в данном месте в данное время произойдет землетрясение, относится к числу случайных событий. Однако подобные события уникальны, поскольку их нельзя воспроизвести. Другой пример, событие, состоящее в том, что данный механизм проработает больше года, является случайным, но уникальным. Конечно, каждый механизм индивидуален по своим качествам, но этих механизмов может изготовляться очень много, причем изготовленных в одних и тех же условиях. Испытания многих сходных объектов дает ту информацию, которая позволяет оценить долю числа появления рассматриваемого случайного события. Таким образом, в теории вероятностей имеют дело с повторением испытаний двух типов: 1) повторение испытаний для одного и того же объекта; 2) испытание многих сходных объектов. В дальнейшем для краткости слово «случайный» будем опускать. События будем обозначать заглавными буквами латинского алфавита: A, B, C и т.д. События A и B называются несовместными, если наступление одного из них исключает возможность появления другого. Например, при подбрасывании монеты могут наступить два события: выпадет "орел" или "решка". Однако, одновременно эти события, при одном подбрасывании, появится не могут. Если в результате испытания возможно одновременное появление событий A и B, то такие события называются совместными. Например, выпадение четного числа очков при подбрасывании игральной кости (событие А) и числа очков, кратного трем (событие В) будут совместными, ибо выпадение шести очков означает наступление и события А, и события В. Событие А называется независимым от события В, если вероятность появления события А не зависит от того, произошло событие В или нет; в противном случае такие события называются зависимыми. Например, вероятность события того. что во второй раз из урны, содержащей белые и черные шары, будет вынут белый шар, не зависит от того, какой шар был вынут в первый раз, если он был возвращен обратно. Однако если первый шар не был возвращен обратно, то результат второго извлечения уже будет зависеть от первого, ибо состав шаров в урне уже изменится в зависимости от результата первого извлечения. Вопрос. Зависимы или нет несовместные события?
Классическое определение вероятности Изложим классическое определение вероятности, служившее основой этой науки со времен ее зарождения в XVII в. (Б. Паскаль, П. Ферма, Я. Бернулли) вплоть до 20-30-х годов XX в., когда теория вероятностей встала на путь аксиоматического метода. Чтобы охарактеризовать вероятность события числом, нужно установить единицу измерения вероятности. Здесь поступают следующим образом: достоверному событию приписывают вероятность, равную единице; невозможному – равную нулю. Таким образом, вероятность P(A) события А должна удовлетворять следующим условиям: 1о. P(A)=1, если А – достоверное событие; 2о. P(A)=0, если А – невозможное событие; 3о. 0<P(A)<1, если А – случайное событие. Классическое определение вероятности основано на понятии равновозможности (или равновероятности). Это понятие относится к числу первичных, не подлежащим формальному определению. Оно лишь поясняется рядом простых и доступных примеров. Например, выпадение одной из сторон монеты или одной из граней игральной кости – равновозможные события. Это утверждение опирается на повседневную практику и симметрию изучаемого объекта. Симметрия возможных исходов чаще всего наблюдается в искусственно организованных опытах, где приняты специальные меры для ее обеспечения (например, тасовка карт или костей домино, которая для того и производится, чтобы каждая из них могла быть выбрана с одинаковой вероятностью; или же приемы случайного выбора группы изделий для контроля качества в производственной практике). В таких опытах подсчет вероятностей производится проще всего. Не случайно первоначальное свое развитие теория вероятностей получила на материале азартных игр. Говорят, что несколько событий образуют полную группу, если в результате опыта неизбежно должно появится хотя бы одно из них. Примеры событий, образующих полную группу: 1) появление "1", "2", "3", "4", "5", "6" очков при бросании игральной кости; 2) "два попадания", "два промаха", "одно попадание" при двух выстрелах по мишени; 3) "появление хотя бы одного белого", "появление хотя бы одного черного" шара при вынимании двух шаров из урны. Несовместные события, образующие полную группу, называются элементарными событиями (или элементарными исходами). Отметим, что события первого и второго примеров являются элементарными, а третьего – нет, т.к. они совместны. Элементарные исходы, в которых интересующее нас событие наступает, называются благоприятствующими этому событию. Например, при бросании одной игральной кости для события, состоящего в том, что выпадет не более двух очков, благоприятствующими элементарными исходами будут выпадение "1" или "2" очков. Классическое определение вероятности: вероятностью события А называется отношение числа m благоприятствующих этому событию исходов к общему числу n всех равновозможныхнесовместных элементарных исходов, образующих полнуюгруппу:
Пример 1.2. В урне находится 5 шаров, из которых 2 белых и 3 черных. Из урны наугад вынимают один шар. Найти вероятность того, что этот шар будет белым. Решение. Обозначим через А интересующее нас событие, т.е. появление белого шара. Общее число всех равновозможных несовместных элементарных исходов, образующих полную группу, равно n=5; из них благоприятствующих событию А будет m=2. Следовательно, вероятность события А равна
Прием непосредственного подсчета вероятностей был положен в основу т.н. "классической" теории вероятностей и долгое время считался универсальным. Опыты, не обладающие симметрией возможных исходов, искусственно сводились к "классической схеме". Несмотря на ограниченную сферу практического применения этой схемы, она все же представляет известный интерес, т.к. именно на ней легче всего познакомится со свойствами вероятностей. "Ахиллесовой пятой" классического определения вероятности является понятие равновозможности, т.е. вопрос о том являются ли рассматриваемые события равновозможными или нет. Ответить на эти вопросы не всегда легко. На заре создания теории вероятностей здесь было наделано немало ошибок. Пример 1.2. (Ошибка Даламбера). Бросаются две монеты. Какова вероятность того, что обе монеты выпадут "гербом" вверх? При решении этой задачи один из выдающихся французских ученых Ж. Даламбер рассуждал следующим образом. При подбрасывании двух монет возможны три случая: А1={два герба}, A2={две решки}, A3={герб и решка}. Эти события находятся в равных условиях, поэтому их вероятности равны 1/3. Однако это неверно. Эти события не являются равновозможными. Последнее событие, как показали наблюдения, вдвое вероятнее каждого из остальных. Решим эту задачу иначе. Для этого рассмотрим следующие события: В1={на первой монете герб, на второй – герб}, В2={на первой монете решка, на второй – решка}, В3={на первой монете герб, на второй – решка}, В4={на первой монете решка, на второй – герб}. Все эти события несовместны, равновозможны и образуют полную группу. Следовательно вероятность события В1 равна 1/4, что совпадает с результатами наблюдений. Пример 1.3. (Задача де Мере). Бросаются три игральные кости. Что вероятнее: получить в сумме выпавших очков 11 или 12? Эта задача была одно из первичных, на основании которых формировались понятия и методы теории вероятностей. Утверждают, что с такой задачей обратился однажды к Б. Паскалю шевалье де Мере. Он заявил Паскалю, что согласно логике обе эти суммы должны появляться одинаково часто, но наблюдения показали, что сумма 11 появляется все же чаще, чем 12. Обоснование де Мере звучит довольно убедительно на первый взгляд. Числа 11 и 12 могут быть разложены на сумму трех целых положительных чисел лишь шестью способами: 11 = 1+5+5 = 1+4+6 = 2+3+6 = 2+4+5 = 3+3+5 = 3+4+4 и 12 = 1+5+6 = 2+4+6 = 2+5+5 = 3+4+5 = 3+3+6 = 4+4+4. Отсюда, по мнению де Мере, вытекает равновероятность обоих сумм. Но почему 11 выпадает все же чаще? Дело в том, что исходы, которые рассматривал де Мере, не являются равновозможными. Необходимо учитывать, на какой из трех костей выпадают те или иные очки. Поэтому комбинация (1,4,6) может возникнуть при шести различных исходах бросания, комбинация (1,5,5) – при трех, а (4,4,4) – при единственном исходе.
Нетрудно подсчитать, что событию А={сумма очков равна 11} благоприятствует 27 исходов, а событию В={сумма очков равна 12} – 25 исходов.
Отсюда видно, что P(A)>P(B).

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
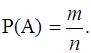



 Поскольку при подбрасывании трех игральных костей возможны 63=216 несовместных и равновозможных исходов, образующих полную группу, то по формуле классической вероятности получаем
Поскольку при подбрасывании трех игральных костей возможны 63=216 несовместных и равновозможных исходов, образующих полную группу, то по формуле классической вероятности получаем