
|
|
Двумерное нормальное распределениеЛЕКЦИЯ 12 Условные характеристики двумерных случайных величин. Функция регрессии. Двумерное нормальное распределение. Корреляционное отношение его свойства. 9.5. Условные характеристики двумерных Известно, что если события A и B независимы, то вероятность совместного появления этих событий равно P(AB) = P(A)P(B), если A и B зависимы, то P(AB) = P(A)PA(B). Аналогичные положения имеют место и для случайных величин. Если случайные величины X и Y независимы, то функция распределения двумерной случайной величины {X,Y} равна произведению функций распределения случайных величин, входящих в систему: F(x,y) = F1(x)×F2(y). (9.12) Выполнение данного равенства является необходимым и достаточным условием независимости двух случайных величин. В случае ДСВ каждый элемент матрицы распределения равен произведению вероятностей соответствующих величин pij = P(X=xi)×P(Y=yj). (9.13) В случае НСВ плотность распределения равна произведению двух плотностей соответствующих величин f(x,y) = f1(x)×f2(y). (9.14) Для описания зависимых случайных величин используют т.н. условные распределения, под которыми понимают распределение одно из случайных величин при условии, что другая приняла вполне определенное значение. Вспомним, как определяется условная вероятность события B при условии наличия события A:
Применим эту формулу для ДСВ {X,Y}:
Пример 9.4. Найти условный закон распределения случайной величины X при условии, что Y=4, для двумерной случайной величины, рассмотренной в примере 9.1. Решение. Поскольку P(Y=4)=0,4, то
Аналогично находятся условные плотности распределения для НСВ:
Здесь f(x|Y=y)ºf(x|y) – условная плотность распределения случайной величины X при условии, что случайная Y приняла значение y; f(y|Y=x)ºf(y|x) определяется аналогично. Пример 9.5. Задана плотность распределения непрерывной двумерной случайной величины {X,Y}
Найти: а) плотности распределения одномерных случайных величин X и Y; б) условные плотности распределения X и Y. Решение. а) Найдем плотность распределения случайной величины X:
Вынесем за знак интеграла множитель
Учитывая, что интеграл Пуассона
Аналогично находим плотность распределения случайной величины Y:
б) Найдем условные плотности распределений случайных величин X и Y:
Условным математическим ожиданием одной из случайных величин, входящих в систему {X,Y}, называется ее математическое ожидание, вычисленное на основе условного распределения:
Условное математическое ожидание M[X|y] есть функция от y: M[X|y] = f(y) (9.19) и называют регрессией X на y. Условное математическое ожидание M[Y|x] есть функция от x: M[X|y] = f(y) (9.20) и называют регрессией Y на x. График функций регрессии называют линиями (кривыми) регрессии. Если случайные величины X и Y независимы, то линии регрессии X на y и Y на x параллельны координатным осям, т.к. математическое ожидание каждой из них не зависят от того, какое значение приняла другая. Аналогично вводятся условные дисперсии: D[X|y] и D[Y|x].
Двумерное нормальное распределение В инженерных приложениях теории вероятностей из систем случайных величин чаще всего встречаются непрерывные системы, имеющие нормальное распределение. В общем виде двумерное нормальное распределение имеет следующий вид
где
Если случайные величины X и Y некоррелированы, т.е. rxy=0, то получим
Это означает, что если составляющие нормально распределенной случайной величины некоррелированы, то плотность такой двумерной случайной величины равна произведению плотностей составляющих:
Отсюда следует независимость случайных величин X и Y. Справедливо и обратное. Итак, для нормально распределенных случайных величин понятия независимости и некоррелированности равносильны. Рассмотрим условные распределения случайных величин X и Y:
Нетрудно убедится, что каждое из условных распределений тоже являются нормальными с условными математическими ожиданиями
и с условными дисперсиями
Таким образом, для системы нормально распределенных случайных величин X и Y линии регрессии M[X|y] и M[Y|x] представляют собой прямые линии, т.е. регрессия для нормально распределенной системы {X,Y} всегда линейна. Причем условные дисперсии являются постоянными величинами.
Корреляционное отношение Если линии регрессии не являются прямыми, то коэффициент корреляции лишь с некоторым приближением может рассматриваться как показатель связи между случайными величинами X и Y. В случае нелинейной связи представляют интерес показатели, характеризующие концентрацию распределения (и, следовательно, тесноту связи) около линий регрессии. Таким показателем является корреляционное отношение, введенное К. Пирсоном. Разброс значений случайной величины Y около математического ожидания my=M[Y] измеряется дисперсией
Этот разброс может быть вызван двумя факторами: 1) влиянием корреляционной зависимости Y от X; 2) влиянием прочих (остаточных) факторов, не влияющих на X. Влияние первого фактора измеряется величиной
т.е. дисперсией линии регрессии относительно математического ожидания my. Влияние второго фактора измеряется величиной
т.е. дисперсией Y относительно линии регрессии. В соответствие со свойствами дисперсии можно записать, что
Корреляционным отношением Y на X называется отношение
Аналогично определяется корреляционное отношение X на Y
Рассмотрим теперь свойства корреляционного отношения. Свойство 1. Корреляционное отношение всегда заключено между 0 и 1, т.е.
Свойство 2. Корреляционное отношение равно 0, тогда и только тогда, когда отсутствует корреляционная зависимость. Действительно, пусть
Отсюда следует, что M[Y|x]=const, т.е. условное математическое ожидание "не реагирует" на изменения значений величины X (линия регрессии параллельна оси Oy). Это и означает, что корреляционная зависимость Y от X отсутствует. Справедливо и обратное утверждение, поскольку при отсутствии корреляционной зависимости M[Y|x]=const, поэтому D[M(Y|x)]=0 и hy/x=0. Свойство 3. Корреляционное отношение равно 1, тогда и только тогда, когда существует функциональная зависимость (y=f(x) и x=g(y)). Действительно, пусть
Но так как дисперсия неотрицательна, то D[Y|x]=0 при любом значении x, а 'это означает, что величина Y принимает единственное значение при котором x, т.е. зависимость Y от X функциональная. Справедливо и обратное утверждение. Из данного свойства следует, что чем ближе корреляционное отношение к единице, тем "концентрация" значений Y к линии регрессии. Свойство 4. Коэффициент корреляции не превосходит по абсолютной величине корреляционное отношение: |r| £ h Отметим, что между hy/x и hx/y нет какой-либо простой зависимости. Например, Y может быть не коррелированно с X и hx/y=0, тогда как другой показатель может быть равен 1, т.е. hy/x=1. Таким образом, поскольку коэффициент корреляции можно рассматривать как линейности регрессии, то величину h2 – r2 можно рассматривать как меру нелинейности регрессии, т.е. отклонения линии регрессии от прямой. Свойство 5. Выполнение равенства hy/x=|rxy| является необходимым и достаточным условием того, чтобы регрессия Y на X была точно линейной. Аналогично и для hx/y. Пример 9.6. Найти корреляционные отношения hy/x и hx/y случайных величин, рассмотренных в примерах 9.1 и 9.4. Решение. Находим корреляционное отношение hy/x:
Проверка: Таким образом,
и
Теперь находим корреляционное отношение hx/y:
Проверка: Таким образом,
и
В последнем случае получилось, что коэффициент корреляции и корреляционное отношение равны. Это объясняется тем, регрессия X на Y линейна.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 ,
,  . (9.15)
. (9.15)
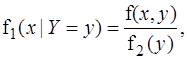
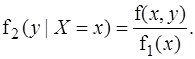 (9.16)
(9.16)

 , не зависящий от переменной интегрирования y, и дополним оставшийся показатель степени до полного квадрата; тогда
, не зависящий от переменной интегрирования y, и дополним оставшийся показатель степени до полного квадрата; тогда
 , окончательно получим плотность распределения случайной величины X:
, окончательно получим плотность распределения случайной величины X: .
. .
.

 ,
,  . (9.17)
. (9.17) ,
,  (9.18)
(9.18) (9.21)
(9.21) .
. .
.
 ,
, .
. ,
,  . (9.21)
. (9.21)
 (9.22)
(9.22) .
. , (9.23)
, (9.23)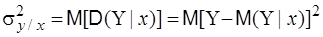 , (9.24)
, (9.24) . (9.25)
. (9.25)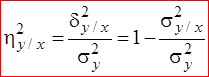 . (9.26)
. (9.26) . (9.27)
. (9.27) .
.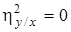 . Тогда
. Тогда
 . Тогда
. Тогда
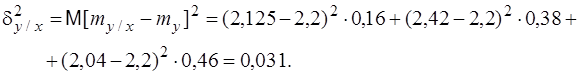
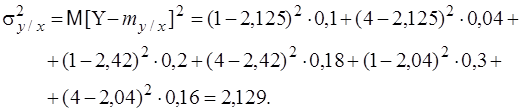


 .
.
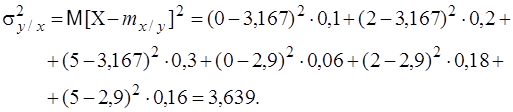

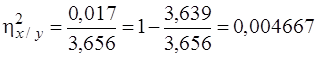
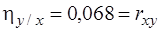 .
.