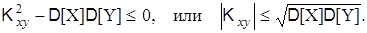|
|
Числовые характеристики двумерных случайных величин12 В качестве числовых характеристик двумерных случайных величин обычно рассматриваются начальные и центральные моменты различных порядков. Начальным моментом порядка k+s двумерной случайной величины {X,Y} число:
В частности, начальные моменты 1-го порядка:
представляют собой математические ожидания случайных величин X и Y. Центральным моментом порядка k+s двумерной случайной величины {X,Y} число:
В частности, центральные моменты 2-го порядка:
представляют собой дисперсии случайных величин X и Y. Особого внимания заслуживает третий центральный момент 2-го порядка:
который называется ковариацией (или корреляционным моментом). для ковариации может быть преобразовано на основании свойств математического ожидания следующим образом:
Из определения ковариации следует, что она имеет размерность, равную произведению размерностей величин X и Y. Другими словами, величина ковариации зависит от единиц измерения случайных величин. По этой причине для одних и тех же двух величин ковариация имеет различные значения в зависимости от того, в каких единицах были измерены величины. Такая особенность ковариации является недостатком этой числовой характеристики, поскольку сравнение ковариаций различных систем случайных величин становится затруднительным. В связи с этим, чтобы устранить указанный недостаток, вводят новую числовую характеристику – коэффициент корреляции:
Пример 9.3. Вычислить числовые характеристики двумерной случайной величины, рассмотренной в пример 9.1. Решение. Используя распределения для X и Y, получим
Рассмотрим теперь свойства коэффициента корреляции. Свойство 1. Коэффициент корреляции двух независимых случайных величин равен нулю. Действительно, пользуясь свойствами математического ожидания (математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий сомножителей) и учитывая, что математическое ожидание отклонения равно нулю, получим для ковариации: Kxy = M[(X–mx)(Y–my)] = M[X–mx]×M[Y–my] = 0. Следовательно, и коэффициент корреляции тоже равен нулю. Отметим, что обратное утверждение неверно. Например, пусть Y=X2 и распределение X симметрично относительно начала координат, т.е. M[X]=0, то M[XY]=M[X3]=0 и M[X]M[Y]=0. Следовательно, Kxy=0 и rxy=0, несмотря на то, что между X и Y имеется функциональная зависимость. Таким образом, если коэффициент корреляции между двумя случайными величинами равен нулю, то утверждение, что эти случайные величины независимы – не всегда справедливо. Это значит, что может существовать система зависимых случайных величин, коэффициент корреляции которых равен нулю. Поэтому вводится понятие коррелированности. Две случайные величины называются коррелированными, если их коэффициент корреляции отличен от нуля; если он равен нулю, то эти величины называются некоррелированными. Итак, из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность. Из независимости двух случайных величин следует их некоррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин. Заранее отметим, что некоррелированность и независимость совпадают только в одном случае, когда случайные величины подчинены нормальному закону распределения. Свойство 2. Коэффициент корреляции rxy двух случайных величин X и Y не превосходит по абсолютной величине единицы, т.е.
Действительно, рассмотрим величину M[(X–mx)+t(Y–my)]2 = D[X]+2tKxy+t2D[Y]. Левая часть равенства неотрицательна при всех значениях t, поэтому квадратный трехчлен, находящийся в правой части, также неотрицателен при всех значениях t. Следовательно, его дискриминант
Разделив обе части неравенства на sxsy, получим |rxy| £ 1. Свойство 3. Коэффициент корреляции двух случайных величин X и Y равен rxy=±1 тогда и только тогда, когда между величинами X и Y существует линейная функциональная зависимость. Очевидно, что если rxy=±1, то тогда дискриминант рассмотренного выше квадратного трехчлена равен нулю, т.е. существуют два равных корня t1=t2. Тогда при t=t1 получим M[(X–mx)+t(Y–my)]2 = 0. Следовательно, (X–mx)+t(Y–my)=0, или X = –t1Y+mx+t1my. Обратное условие, если имеется линейная зависимость, тогда она всегда может быть задана в данном виде при некотором t. Это означает существование равных корней t1=t2 квадратного трехчлена и, следовательно, справедливо равенство rxy=±1. Итак, при возрастании |rxy| от 0 до 1 корреляционная связь увеличивается, а при |rxy|=1 она становится линейной функциональной зависимостью. Другими словами, коэффициент корреляции можно рассматривать как меру линейной зависимости между двумя случайными величинами X и Y.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
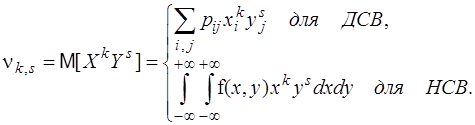 (9.7)
(9.7)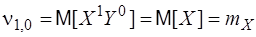 ,
, 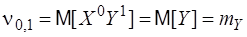 ,
,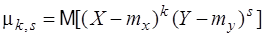 . (9.8)
. (9.8) ,
,  ,
, , (9.9)
, (9.9)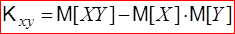 . (9.10)
. (9.10)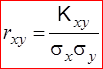 . (9.11)
. (9.11)
 .
.