Различительная способность заданий

Выбор критерия.Под различительной способностью задания понимают ту степень, с какой оно правильно дифференцирует тестируемых по поведению, для измерения которого и предназначен данный тест. В тех случаях, когда тест в целом можно °Ценить посредством критериальной валидизации, входящие в него задания также

Часть 2. Технические и методологические принципы

могут оцениваться и отбираться на основе их связей с тем же внешним критерием. Этим путем особенно часто шли при разработке некоторых тестов личности и интересов, обсуждаемых в главах 13 и 14. Кроме того, этот метод обычно используют при выборе вопросов для включения в биографические вопросники, которые в типичном случае охватывают разнородное собрание сведений о происхождении и жизненном пути конкретных лиц. Применительно к измерительным инструментам этого типа мы не располагаем никаким априорным основанием для классификации ответов на правильные и неправильные или для приписывания им весовых коэффициентов, кроме сравнения с критериальным статусом лиц, дающих эти ответы. Из первоначального банка заданий (вопросов) сохраняются те, которые лучше всего дифференцируют обследуемых лиц, отнесенных к различным критериальным категориям, таким как различные профессии или психиатрические синдромы. Часто критериальные группы состоят из достигших успеха и потерпевших неудачу в университетском курсе, программе профподготовки или конкретном виде работы.

В предметно-ориентированном тестировании уровня знаний, умений и навыков, обсуждавшемся в главе 3, задания могут оценивать путем сравнения выполнения каждого из них лицами, различающимися объемом полученного обучения в соответствующей области (Panell, & Laabs, 1979; L. A. Shepard, 1984). Обычной практикой является сравнение долей лиц, давших правильные ответы на задания до и после прохождения курса обучения. Поскольку эти тесты используют для определения того, достигли ли обучаемые заданного уровня владения предметом или деятельностью, индивидуальные различия в результатах при однократном проведении теста сведены к минимуму. При этих условиях внутренний анализ заданий (предполагающий их сравнение друг с другом) не будет иметь смыла и поэтому нужен внешний критерий, такой как объем обучения в конкретной области.

В других типах тестов достижений, как и во многих тестах способностей, различительная способность заданий обычно исследуется по отношению к суммарному показателю самого теста.¹ Для образовательных тестов достижений внешний критерий в типичных случаях недоступен. Что касается тестов способностей, растущее внимание исследователей к конструктной валидности и методам ее установления делает суммарный показатель по тесту вполне уместным критерием для отбора заданий. На начальных этапах разработки теста суммарный показатель обеспечивает первое приближение к мере изучаемой способности, черты или конструкта.

Рассмотрим более подробно следствия выбора заданий на основе внешнего критерия и на основе суммарного тестового показателя. Первый путь ведет к максимизации валидности теста относительно внешнего критерия, а второй — к максимизации внутренней согласованности или однородности теста. При определенных условиях эти два подхода могут приводить к противоположным результатам: задания, выбираемые по соображениям внешней валидности, оказываются как раз теми заданиями, которые отбрасываются исходя из соображений внутренней согласованности. Предположим, что предварительная форма теста академических способностей состоит из 100 арифметических и 50 словарных заданий. Чтобы произвести отбор заданий из этой исход-

¹ Корреляции «задание — тест» всегда несколько завышены из-за совместного действия дисперсии ошибок и специфической дисперсии конкретного задания и теста, частью которого оно является. Для корректировки этого эффекта «часть — целое» имеются специальные формулы (Guilford & Fruchter, 1978, p. 165-167).

Глава 7. Анализ заданий

ной совокупности с целью повышения внутренней согласованности теста, необходимо будет вычислить некий показатель согласования между выполнением каждого задания и суммарным показателем по 150 заданиям. Очевидно, что такой показатель, в общем, будет выше для арифметических, чем для словарных заданий, так как суммарный показатель основан на в два раза большем числе арифметических заданий. Если мы захотим сохранить 75 «лучших» заданий в окончательной форме этого теста, то большинство из них, по всей вероятности, окажутся арифметическими. Но с точки зрения внешнего критерия академической успеваемости, словарные задания, возможно, были бы более валидными предикторами, чем арифметические. Если дело обстоит именно так, то анализ заданий привел бы к снижению, а не повышению валидности теста.

Практика отбрасывания заданий, имеющих низкие корреляции с суммарным показателем, дает нам способ повышения однородности или «очищения» теста. Благодаря применению этой процедуры сохраняются задания с наибольшими средними интеркорреляциями. Данный метод отбора заданий будет повышать валидность теста только в тех случаях, когда первоначальная совокупность заданий измеряет одно-единственное свойство и когда это свойство присутствует в критерии или оцениваемом конструкте. Однако некоторые типы тестов измеряют комбинацию свойств, требуемых сложным критерием. В таком случае очищение теста может привести к сужению зоны охвата тестом его критерия и тем самым к снижению валидности.

Отбор заданий с целью максимизации критериальной валидности теста можно уподобить отбору тестов для получения наибольшей валидности батареи. Напомним (глава 6), что вклад теста в валидность батареи тем больше, чем выше его корреляция с критерием и чем ниже корреляция с другими тестами батареи. Если этот принцип применить к отбору заданий, то наиболее удовлетворительными будут задания с самыми высокими показателями внешней валидности и самыми низкими коэффициентами внутренней согласованности. Так, задание, имеющее высокую корреляцию с внешним критерием, но относительно низкую — с суммарным показателем теста, было бы предпочтительнее задания, имеющего высокую корреляцию и с критерием, и с тестом в целом, ибо первое задание, по-видимому, измеряет некоторый аспект критерия, не охватываемый в должной мере оставшейся частью т;еста.

Казалось бы, при отборе заданий можно использовать те же методы, что и при выборе тестов для включения в батарею. В частности, можно было бы вычислить корреляцию каждого задания с критерием и со всеми остальными заданиями. Лучшим заданиям, отобранным таким путем, можно было бы затем приписать веса на основе построенного уравнения регрессии. Такая процедура, однако, неосуществима и теоретически несостоятельна. Дело не только в большом объеме необходимых для этого вычислений, но и в том, что корреляции между заданиями сильно зависят от колебаний выборки и найденные по ним коэффициенты регрессии были бы слишком неустойчивы, чтобы на них можно было основывать отбор заданий. Есть и более серьезное возражение против такой процедуры: получившийся в результате тест оказался бы настолько неоднородным по содержанию, что это исключило бы всякую возможность смысловой интерпретации тестового показателя.

Валидность относительно внешнего критерия и внутренняя согласованность являются важными целями конструирования теста. Относительное значение, придаваемое каждой из них, меняется в зависимости от характера и назначения теста. Применительно ко многим задачам тестирования удовлетворительным компромиссным ре-

Часть 2. Технические и методологические принципы

шением будет сгруппировать относительно однородные задания в отдельные тесты или субтесты, каждый из которых охватывает какой-то один аспект внешнего критерия. Тем самым широта охвата достигается за счет разнообразия тестов, каждый из которых дает более или менее однозначный показатель, а не за счет разнородности заданий в рамках одного теста. При таком подходе задания с низкими индексами внутренней согласованности не отбрасывались бы, а выделялись в особые группы. В результате этого внутри каждого субтеста или группы заданий можно было бы достичь довольно высокой внутренней согласованности.

Статистические индексы различительной способности задания.Поскольку обычно регистрируется лишь факт выполнения или невыполнения задания, измерение различительной способности задания, как правило, связано с соотнесением дихотомической переменной (задания) и непрерывной переменной (критерия). В некоторых ситуациях критерий тоже может быть дихотомической переменной, как в случае окончания или отчисления из колледжа, успеха или неудачи в работе. Кроме того, непрерывный критерий в целях анализа всегда можно преобразовать в дихотомический.

Было разработано свыше 50 индексов различительной способности задания, которые и в настоящее время используют при конструировании тестов. Одно из различий между ними относится к применимости этих индексов к дихотомическим или непрерывным мерам. Кроме того, среди индексов, применимых к дихотомическим переменным, одни предполагают непрерывность и нормальное распределение измеряемого с помощью теста свойства, которое подвергается искусственной дихотомизации при обработке результатов тестирования, тогда как другие основаны на предположении об истинной дихотомии изучаемого свойства. Другое различие касается связи трудности задания с различительной способностью. Некоторые индексы оценивают различительную способность задания независимо от его трудности, а некоторые дают более высокую оценку различительной способности заданий, уровень трудности которых приближается к 0,50, и более низкие оценки для крайне легких и крайне трудных заданий.

Независимо от способа получения и исходных допущений большинство индексов различительной способности задания дают весьма сходные результаты (Oosterhof, 1976). Хотя числовые значения индексов могут различаться, на их основе сохраняются или отвергаются в основном одни и те же задания. В действительности, колебание данных о различительной способности задания от выборки к выборке в целом больше, чем при использовании различных методов получения таких данных.

Использование контрастных групп.Распространенный метод анализа заданий — сравнение долей выполнивших задание в двух контрастных по выполению критерия группах. Когда критерий измеряется в непрерывной шкале (как в случае годовых оценок, оценок работы руководителями, показателей производительности труда или суммарных показателей по определенному тесту), верхняя (В) и нижняя (Я) критериальные группы формируются из лиц, занимающих положение на соответствующих краях распределения. Очевидно, что чем ближе к краям распределения будут эти группы, тем резче будет выражено различие. Однако использование предельно контрастирующих групп, представленных, скажем, верхними и нижними 10 % распределения, снизило бы надежность результатов из-за малого числа используемых случаев. При нормальном распределении оптимальная точка, в которой эти два условия уравновеши-

Глава 7. Анализ заданий

ваются, достигается при верхних и нижних 27 % распределения (Т. L. Kelley, 1939). Когда распределение более плоско, чем нормальная кривая, оптимальный процент несколько больше 27 % и равен почти 33 % (Cureton, 1957b,). В случае малых групп — таких, как обычный класс, — ошибка выборки настолько велика, что можно рассчитывать только на грубые статистические оценки. Поэтому здесь не приходится заботиться о точном проценте случаев в двух контрастных группах. Приемлема любая цифра между 25 и 33 %.

При разработке стандартизованных тестов используются большие и нормально распределенные выборки, и в этом случае обычно работают с верхними и нижними 27 % распределения критериальных показателей. Многие таблицы и номограммы, облегчающие вычисление индексов различительной способности заданий, составлены на основе допущения о соблюдении «правила 27 %». По-видимому, распространение быстродействующих компьютеров позволит со временем заменить различные вспомогательные приемы, разработанные для облегчения анализа заданий, более точными и совершенными методами. Современная вычислительная техника позволяет анализировать результаты всей выборки, не ограничиваясь верхним и нижним краями распределения.

Упрощенный анализ заданий в случае малых групп.Поскольку анализ заданий часто проводится при работе с малыми группами, например с учащимися одного класса, отвечающими на контрольный вопросник, рассмотрим прежде всего простую процедуру, особенно подходящую для такой ситуации. Предположим, в классе всего 60 человек, из которых отобрано 20 учеников (33 %) с самыми высокими и 20 (33 %) — с самыми низкими тестовыми показателями. Разложим листки с ответами на три стопки, принадлежащие верхней (В), средней (С) и нижней (Н) группе. Теперь нам нужно определить, сколько правильных ответов в каждой из этих групп было дано на каждый вопрос. Для этого выпишем в столбик номера вопросов, оставив справа место для трех колонок, которые обозначим буквами В, С и Н. Возьмем из стопки В любой листок и в колонке В проставим палочки против тех вопросов, на которые данный ученик ответил правильно. Это нужно проделать для каждого из 20 листков группы В, затем для 20 листков группы С и, наконец, для всех листков группы Н. Подсчитаем теперь палочки и запишем результаты для каждой группы так, как это показано в табл. 7-1 (для краткости в ней приведены цифры только по первым семи вопросам). Приблизительный индекс различительной силы любого из вопросов находится вычитанием числа учеников, правильно ответивших на него в группе Н, из числа учеников, правильно ответивших на него в группе В. Эти разности (В—Н) приведены в последней колонке табл. 7-1. На основе тех же исходных данных можно получить меру трудности вопроса, для чего нужно сложить число справившихся с каждым вопросом во всех трех критериальных группах (В + С + Н).

Анализ табл. 7-1 выявляет 4 сомнительных задания, которые заслуживают последующего рассмотрения или обсуждения в классе. Два вопроса, 2-й и 7-й, были выделены потому, что один из них слишком легок (56 из 60 учеников ответили на него правильно), а другой слишком труден (всего 5 правильных ответов). Вопросы 4-й и 5-й, хотя и удовлетворительны с точки зрения уровня трудности, тем не менее обнаруживают отрицательную и нулевую различительную способность соответственно. К этой категории мы также отнесли бы любые вопросы с очень малыми положительными значениями разности (В — Н), примерно от 3 и менее единиц для сравниваемых

Часть 2. Технические и методологические принципы

Таблица 7-1 Упрощенная процедура анализа заданий: число лиц, давших правильный ответ в каждой критериальной группе

* Задания, выбранные для последующего обсуждения

групп примерно того же размера. Имея дело с большими группами, можно ожидать и больших различий (В—Н), возникающих случайно при выполнении задания, не обладающего различительной способностью.

Цель анализа заданий теста, подготовленного учителем, состоит в выявлении дефектов как в самом тесте, так и в преподавании. Одного обсуждения сомнительных заданий с классом часто достаточно для того, чтобы обнаружить проблему. Если вопрос сформулирован неудачно, его можно перестроить или вовсе изъять при последующем тестировании. Обсуждение, однако, может обнаружить, что вопрос составлен правильно, но у учеников нет надлежащего понимания данной темы. В этом случае тема может быть разобрана заново и пояснена подробнее. При отыскании менее очевидного источника затруднений часто полезно провести дополнительный анализ (см. табл. 7-2) хотя бы тех вопросов, что были отобраны для обсуждения. В табл. 7-2 приводится число учеников из групп В и Н, выбравших каждый из пяти вариантов ответа на эти вопросы.

Хотя вопрос 2 и был включен в табл. 7-2, мы мало что можем узнать о нем из приведенных здесь данных о частоте ошибочных ответов, поскольку неправильный выбор сделали лишь 4 ученика из группы Н и никто — из группы В. Однако обсуждение этого вопроса с учениками, возможно, поможет определить, действительно ли вопрос слишком легок и не представляет особой ценности, или какой-то недостаток формулировки позволяет сразу же находить правильный ответ, или же, наконец, это полезный вопрос, но относится к хорошо проработанной с учителем и прочно усвоенной теме занятий. В первом случае вопрос, видимо, следует изъять, во втором — переформулировать, а в третьем — оставить без изменения.

Данные по вопросу 4 показывают, что третий вариант ответа содержит в себе нечто такое, что заставляет 9 учеников из группы В предпочесть его правильному (второму) варианту. В чем здесь дело, нетрудно установить, попросив этих учеников обосновать свой выбор. Ошибки в ответах на вопрос 5, видимо, объясняется неудачностью фор^-мулировки либо самого вопроса, либо варианта правильного ответа, так как ошибоч-

Глава 7. Анализ заданий

Таблица 7-2 Анализ ответов на отдельные вопросы

Примечание. Правильные варианты ответов выделены жирным шрифтом

ные выборы учащихся равномерно распределились по четырем вариантам ложного ответа. Вопрос 7 необычно труден: 15 человек из группы В и вся группа Н ответили на него неправильно. Несколько больший выбор третьего (ложного) варианта в данном случае указывает на его внешнюю привлекательность, особенно для легче вводимых в заблуждение членов группы Н. Аналогично отсутствие правильных ответов (вариант 1) в группе Н говорит о том, что плохо осведомленному ученику эта альтернатива на первый взгляд кажется ошибочной. Разумеется, оба эти свойства желательны для хорошего тестового задания. Обсуждение в классе могло бы показать, что вопрос 7 — это хороший вопрос, относящийся, однако, к теме, усвоенной лишь несколькими учениками данного класса.

Индекс различительной способности.Если число справившихся с определенным заданием в верхней (В) и нижней (Н) критериальных группах выразить в процентах, разность между ними дает нам индекс различительной способности задания, интерпретируемый независимо от размера выборки, на которой он был получен. Этот индекс неоднократно обсуждался в психометрической литературе (см., например, Ebel, 1979; A. P.Johnson, 1951; Oosterhof, 1976) и обозначался то как U — U, то как ULI или ULD, а то и просто D. Несмотря на свою простоту, этот индекс, как было показано, хорошо согласуется с другими, более сложными мерами различительной способности задания (Engelhart, 1965; Oosterhof, 1976). Вычисление D можно проиллюстрировать на примере данных, приведенных в табл. 7-1. Сначала число лиц, справившихся с каждым заданием в группах В и Н, переводится в проценты. Разность между соответствующими процентами и есть индекс различительной способности (D), значения которого для семи анализируемых нами заданий приведены в табл. 7-3. D может принимать любое значение между ±100. Если все члены группы В справились и никто из группы Н не справился с заданием, то D = 100. И наоборот, если группа Н справилась, ^а группа В не справилась с заданием, то D = -100. Если же процент справившихся с заданием в обеих группах одинаков, то D = 0.

Первые буквы английских слов Upper (верхний) и Lower (нижний). — Примеч. науч. ред.

Часть 2. Технические и методологические принципы

Таблица 7-3 Вычисление индекса различительной способности задания

Примечание. Использованы данные из табл. 7-1

Как и другие индексы различительной способности заданий, индекс D зависит от трудности задания, но в отличие от них обнаруживает смещение в пользу промежуточных уровней трудности. В табл. 7-4 приведены максимально возможные значения D для заданий с различным процентом правильных ответов. В тех случаях, когда 100 % или 0 % всей выборки справились с заданием, никакого различия в процентах справившихся с этим заданием в группах В и Н просто не может быть, — и потому D = 0. С другой стороны, если с заданием справились 50 % членов выборки, не исключено, что все они принадлежат к группе В, и тогда D = 100 (100 — 0 = 100). Если же справившихся оказалось 70 %, то максимальное значение, которое индекс D мог бы принять в этом случае, можно пояснить следующим образом: (В) 50/50 •» 100 %; (Н) 20/50 = = 40 %; D = 100 — 40 = 60. Напомним, что для большинства целей тестирования предпочтение отдается заданиям, уровень трудности которых близок к 0,50. Поэтому индексы различительной способности, принимающие максимальные значения при этом уровне трудности, часто более других подходят для отбора заданий.

Таблица 7-4 Связь максимальной величины индекса D с трудностью задания

КоэффициентФ. Многие индексы различительной способности заданий выражают связь между заданием и критерием в виде коэффициента корреляции. Одним из них является коэффициент ф (фи). Вычисляемый по четырехпольной таблице, ф основан на соотношении долей справившихся и не справившихся с заданием в верхней (В) и нижней (Н) критериальных группах. Подобно всем коэффициентам корреляции, ф принимает значения в интервале от +1,0 до -1,0 и предполагает подлинную дихотомию как ответов на задание, так и критериальной переменной. Следовательно,

Глава 7. Анализ заданий

он применим лишь к тем дихотомическим условиям, при которых был найден, и не может быть обобщен на какие-то глубинные, скрывающиеся за ними отношения между измеряемыми данным заданием свойствами и критерием. Как и индекс D, коэффициент ф принимает наибольшие значения для заданий средних уровней трудности, когда дихотомия близка к соотношению 50 : 50.

Уровень значимости коэффициента ф нетрудно определить благодаря его связи и с критерием x², и с Z-критерием (критическим отношением). С помощью последнего можно найти минимальное значение ф, достигающее статистической значимости на уровне 0,05 или 0,01, по следующим формулам:

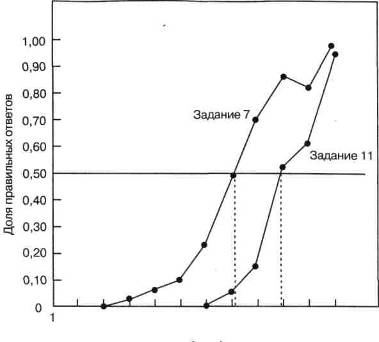
В этих формулах N— суммарное число испытуемых в обеих критериальных группах. Так, если бы группы В и Я содержали по 50 человек, то Мбыло бы равно 100, и минимальное значение коэффициента ф, значимое на уровне 0,05, равнялось бы

1,96: Vl00 = 0,196. Следовательно, любое задание с коэффициентом ф, равным или превышающим 0,196, коррелировало бы с критерием на уровне значимости 0,05.

Бисериальная корреляция.В качестве последнего примера широко используемой меры различительной способности задания можно рассмотреть бисериальную корреляцию (rbis), отличающуюся от ф в двух важных отношениях. Во-первых, rbis предполагает непрерывное и нормальное распределение свойств, лежащих в основе дихотомической формы ответа на задание и критериальной переменной. Во-вторых, rbisкак мера связи между заданием и критерием не зависит от трудности задания.

Для оценки бисериальной корреляции нужно знать средние критериальных показателей справившихся и не справившихся с заданием и соответствующее SD, вычисленное по показателям всех членов критериальной группы, а также долю лиц, справившихся (либо не справившихся) с заданием в этой группе. Формулы для вычисления r_bis приведены в большинстве учебников по статистике (например, Guilford, & Fruchter, 1978, pp. 304-306). Стандартную ошибку rbisможно вычислить с помощью простой формулы, включающей выражения из формулы для вычисления r_his. Следует Добавить, что наличие вычислительной техники позволяет сразу получать значения rbisи их стандартных ошибок.

Теория «задание — ответ»

Регрессия «задание — тест».Трудность и различительную способность задания можно одновременно отобразить в виде линии регрессии «задание — тест». В целях Иллюстрации рассмотрим гипотетический тест из 12 заданий, требующих коротких ответов в свободной форме, наподобие словарных тестов в проводимых индивидуально шкалах интеллекта. В табл. 7-5 приведены доли лиц с разным суммарным бал-Лом по этому тесту, ответивших правильно на каждое из двух заданий. Эти же данные Представлены в виде графиков на рис. 7-5.

Часть 2. Технические и методологические принципы

Уровень трудности каждого задания можно определить как его 50 %-ный порог, так же как это обычно делается при установлении сенсорных порогов в психофизике. Это сделано на рис. 7-5 с помощью простейших геометрических построений: из точек пересечения кривых двух заданий с горизонтальной линией, соответствующей 50 % правильных ответов, опускают два перпендикуляра на ось абсцисс, по которой отложены суммарные тестовые показатели (баллы). Из этих построений хорошо видно, что у тех, кто набрал по этому тесту в сумме примерно 8 баллов, шансы справиться с заданием 7 равны 50:50, а у набравших примерно 10 баллов такие же шансы справиться с заданием 11. На различительную силу каждого задания указывает крутизна соответствующей кривой: чем круче кривая, тем выше корреляция выполнения задания с суммарным показателем по тесту и больше величина индекса различительной способности задания. Судя по внешнему виду кривых, различительная способность заданий 7 и 11 примерно одинакова.

Изучение регрессий «задание—тест», подобных изображенным на рис. 7-5, дает возможность наглядно представить, насколько эффективно работает то или иное задание теста. Такие графики не только объединяют информацию о трудности и различительной способности задания, но также дают полную картину отношений между выполнением каждого задания и суммарным тестовым показателем. Например, задание 7 обнаруживает инверсию, поскольку те, кто набрал в сумме 10 баллов, справляются с этим заданием лучше тех, кто набрал 11 баллов по данному тесту. Когда подобные результаты получены на малой выборке, этой инверсией можно было бы пренебречь; однако она иллюстрирует вид информации, которую могут выявить данные такого анализа заданий.

Несмотря на очевидные достоинства, такие графики являются довольно грубыми и мало пригодны для математической обработки, точной оценки и строгого отбора заданий. Этот подход послужил отправной точкой для разработки весьма тонких и сложных типов анализа заданий, которые начали завоевывать внимание в 1970-х и начале 1980-х гг. Причину их растущей популярности, безусловно, следует искать в

Таблица 7-5 Гипотетические данные для построения регрессии «задание—тест»

Глава 7. Анализ заданий

2 3 4 5 6 7 8 9 10 11 12 Суммарный балл

Рис.7-5. Регрессия «задание—тест» для заданий 7 и 11 (по данным табл. 7-5)

стремительном расширении доступа к быстродействующим компьютерам, без которых связанные с такими типами анализа вычислительные задачи потребовали бы несоразмерных затрат времени и средств. С составлением компьютерных программ для целого ряда предложенных моделей анализа заданий, практическое применение этих тонких методов стало легко осуществимым. Важнейшие особенности этого подхода будут охарактеризованы в следующих разделах.

Теория «задание — ответ» (IRT): основные черты.¹Рассматриваемый математический подход — теория «задание — ответ» — также известен под названиями «теория латентных черт» и «теория характеристических кривых задания» (item characteristic curve theory или, сокращенно, ICC теория). Главная особенность этого подхода состоит в том, что выполнение задания ставится в связь с оценкой величины «латентной черты» респондента, обозначаемой греческой буквой (тэта). В этом контексте под «латентной чертой» понимается статистический конструкт, за которым не стоит никакой психологической или физиологической сущности, обладающей независимым существованием. В когнитивных тестах латентной чертой обычно называют измеряемую тестом способность (ability). Суммарный показатель по тесту часто принимают за начальную оценку такой способности.

Ясный обзор методологии IRT и ее приложений см. в Hambleton et al. (1991). Обзоры технических аспектов IRT и ее критические оценки можно найти в Hambleton (1989), Drasgow & Hulin (1990). ⁰ внедрении IRT в психометрику см. Lord (1980), D.J. Weiss (1983), D.J. Weiss & Davidson (1981).

Чисть 2. Технические и методологические принципы

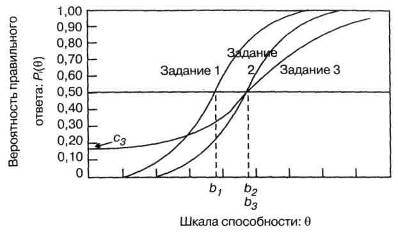
Рис. 7-6. Гипотетические характеристические кривые для трех заданий

Характеристические кривые заданий строятся на основе математически выведенных функций, а не по эмпирическим данным, используемым при построении регрессионных кривых «задание—тест». В различных моделях IRT используются разные математические функции, так как эти модели основаны на разных наборах допущений. В одних моделях — это интегральные кривые нормального распределения; в других — логистические функции, позволяющие использовать некоторые математически удобные свойства логарифмических отношений. Вообще, применение различных моделей этого рода дает по существу сходные результаты, при условии, что лежащие в их основе допущения не нарушаются в конкретных ситуациях. На рис. 7-6 изображены характеристические кривые для трех гипотетических заданий. Осью абсцисс задана шкала способности (9), оцениваемой по суммарному тестовому показателю и другой информации об ответах на тест в конкретной выборке. Ось ординат дает значения Р. (6) — вероятности правильного ответа на f-e задание как функции от положения респондента на шкале способности (6). Эта вероятность находится по данным о доле респондентов, отнесенных к разным уровням изучаемой способности, которые справились с i-м заданием.

В полной, трехпараметрической модели каждая ICC описывается тремя параметрами, выведенными математически из эмпирических данных. Параметр различающей мощности (или различительной способности) задания (а,)свидетельствует о наклоне кривой. Он обратно пропорционально связан с тем расстоянием, на которое нужно переместиться по континууму способности (0), чтобы повысить Р. (0). Чем больше величина а_;, тем круче наклон кривой. На рис. 7-6 задания 1 и 2 имеют одинаковую величину а,, или различающую мощность; задание 3 характеризуется меньшим a_t, так как его кривая поднимается медленнее. Параметр трудности задания Ф) соответствует точке на оси способности, в которой вероятность правильного ответа, Р (0), равна 0,50. Из рисунка хорошо видно, что задания 2 и 3 имеют одинаковый параметр b_f и, значит, одинаковую трудность, а задание 3 легче и, следовательно, требует меньшей способности для достижения вероятности правильного ответа Р. (0) "" = 0,50. Модели IRTдля заданий с множественным выбором часто включают третий

Глава 7. Анализ заданий

параметр — так называемый параметр угадывания (с,).' Он отображает вероятность случайного появления правильного ответа. При использовании заданий с множественным выбором даже у обследуемых с самими низкими уровнями способности вероятность дать правильный ответ выше нуля. На рис. 7-6 это видно на примере задания 3, чья асимптота снизу проходит значительно выше нуля.

В типичных случаях для вычисления оценок параметров задания и оценок способности используют итеративные методы или, как их еще называют, методы последовательного приближения; аппроксимации повторяются до тех пор, пока оценки не становятся устойчивыми. В добавление к получению математически уточненных индексов трудности и различительной способности заданий методы IRT дают ряд других преимуществ. Важной особенностью этого подхода является исследование надежности и ошибки измерения при помощи информационных функций заданий (item information functions). Эти функции, вычисляемые для каждого задания, служат надежной опорой при выборе заданий в процессе конструирования теста. Информационная функция задания учитывает все его параметры и показывает его эффективность как средства измерения на различных уровнях способности.

Наиболее широко разрекламированный вклад моделей /ЙГимеет отношение к получаемым с их помощью результатам, которые не зависят от характера выборки, что в специальной литературе описывается как инвариантность параметров задания (in-variance of item parameters). Основная идея теории «задание — ответ» как раз и состоит в том, что параметры задания не должны изменяться при их вычислении в группах, различающихся по уровню способности. Кроме того, это означает, что как группы, так и отдельных людей можно тестировать с помощью разных наборов заданий, которые соответствуют их уровням способности, а их показатели можно сравнивать напрямую. Тестовый показатель каждого конкретного человека основывается не только на количестве, но и на заранее установленном уровне трудности выполненных им правильно заданий.

Не нашли, что искали? Воспользуйтесь поиском по сайту: