
|
|
Решение нелинейных уравненийЛабораторная работа № 3. Решение линейных и квадратных уравнений Цель работы: изучить возможности Excel для решения математических задач.
Рассмотрим решение следующих типов уравнений: 1) линейных вида 2) квадратных вида В качестве инструмента для решения применяется программа Microsoft Excel. Практическая часть
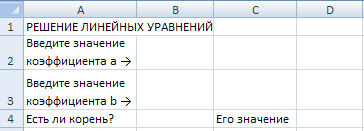
Задание 1. Решение линейных уравнений вида 1.Запустите программу Microsoft Excel. 2.Значения коэффициентов a и b будем водить соответственно в ячейки B2 и B3, а информацию об этом запишем в ячейки A2 и A3 (рисунок 1). В ячейке B4 будем выводить информацию о том, имеет ли заданное пользователем уравнение корень или нет, и в случае положительного ответа значение корня укажем в ячейке D4.
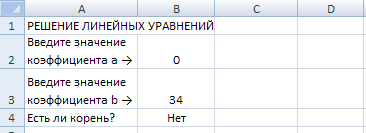
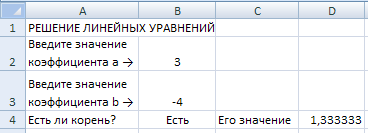
Рисунок 1. Образец заполнения Формула в ячейке B4 должна иметь вид: =ЕСЛИ(B2<>0;"Есть";"Нет") – а в ячейке С4: =ЕСЛИ(B2<>0;"Его значение";"") – а в ячейке D4: =ЕСЛИ(B2<>0;-B3/B2;"") Вид фрагмента листа для двух возможных случаев приведен на рисунке 2 и рисунке 3.
Рисунок 2. Пример работы
Рисунок 3. Пример работы 3.Очевидно, что при представленном оформлении листа в ячейке B4 сообщение Нет будет выводиться даже в случае, когда коэффициент a вообще не задан, что не совсем корректно. Чтобы устранить этот недостаток, можно использовать функцию ЕПУСТО(), возвращающую значение ИСТИНА, если в ячейке, адрес которой указан в качестве аргумента функции в скобках, значение отсутствует. С использованием указанной функции формулы в ячейках A4, B4, C4 и D4 будут иметь вид (соответственно): =ЕСЛИ(ЕПУСТО(B2);"";"Есть ли корень?") =ЕСЛИ(ЕПУСТО(B2);"";ЕСЛИ(B2<>0;"Есть";"Нет")) =ЕСЛИ(ЕПУСТО(B2);"";ЕСЛИ(B2<>0;"Его значение";"")) =ЕСЛИ(ЕПУСТО(B2);"";ЕСЛИ(B2<>0;-B3/B2;"")) 4.Сохраните выполненное задание под именем Лаб_3_Задание_1.
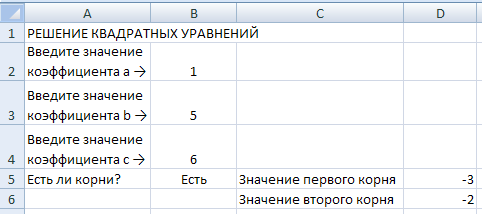
Задание 2. Решение квадратных уравнений вида 1.Запустите программу Microsoft Excel. 2.Значения коэффициентов a, b и c будем задавать соответственно в ячейках B2, B3 и B4, а информацию об этом запишем в ячейки A2, A3, A4 (рисунок 4). В ячейке B5 будем выводить информацию о том, имеет ли заданное пользователем уравнение корень или нет, и в случае положительного ответа значение корней укажем в ячейках D5 и D6.
Рисунок 4. Пример работы 3.Очевидно, что для решения квадратного уравнения следует рассчитывать его дискриминант. Однако значение дискриминанта уравнения является вспомогательным и для пользователя может быть скрыто, например, выведено за пределы страницы, оформлено белым цветом и т.п. Мы вычисляем значение дискриминанта за пределами страницы, например в ячейке M3. Формула для его расчета следующая: =B3^2-4*B2*B4. А формулы в ячейках B5, C5, C6, D5 и D6 соответственно: =ЕСЛИ(M3<0;"Нет";"Есть") =ЕСЛИ(M3>=0;"Значение первого корня";"") =ЕСЛИ(M3>=0;"Значение второго корня";"") =ЕСЛИ(M3>=0;(-B3-M3^0,5)/(2*B2);"") =ЕСЛИ(M3>=0;(-B3+M3^0,5)/(2*B2);"") 4.Сохраните выполненное задание под именем Лаб_3_Задание_2.
Решение нелинейных уравнений Рассмотрим задачу в общем виде. Пусть дано уравнение с одним неизвестным вида При использовании приближенных методов решения уравнений приходится решать две задачи: 1) отделение корней; 2) уточнение корней с заданной точностью. Задача отделения корней заключается в следующем: необходимо найти достаточно малые числовые промежутки, в каждом из которых заключен один и только один корень уравнения. Найти промежутки, в которых содержится один корень уравнения (отделить корни), можно следующими способами: 1. Составить таблицу значений функции 2. Уравнение 3. Построить график функции Перечисленные способы позволяют визуально приблизительно определить корень или корни (если их несколько) уравнения. Если все корни не удалось увидеть на одном графике, то можно построить несколько графиков при разных интервалах варьирования значения переменной в уравнении. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ;
; ;
;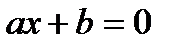
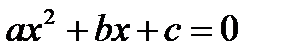
 . Число
. Число  называется корнем уравнения, если при подстановке его вместо х уравнение превращается в верное числовое равенство. Заметим, что корни уравнения могут быть как действительными, так и комплексными. Далее речь пойдет только о нахождении действительных корней.
называется корнем уравнения, если при подстановке его вместо х уравнение превращается в верное числовое равенство. Заметим, что корни уравнения могут быть как действительными, так и комплексными. Далее речь пойдет только о нахождении действительных корней. на определенном промежутке изменения аргумента x, и если окажется, что для соседних значений аргументов значения функции имеют разные знаки, то корень уравнения находится между ними.
на определенном промежутке изменения аргумента x, и если окажется, что для соседних значений аргументов значения функции имеют разные знаки, то корень уравнения находится между ними. заменить равносильным
заменить равносильным  . Построить графики функций
. Построить графики функций  и
и  . Искомый корень будет являться точкой пересечения этих графиков.
. Искомый корень будет являться точкой пересечения этих графиков. точки пересечения графика с осью Ox – корень уравнения, т.е.
точки пересечения графика с осью Ox – корень уравнения, т.е.  .
.