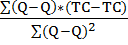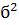Метод наименьших квадратов

Для распределения общих затрат на переменные и постоянные методом наименьших квадратов необходимы стратегические данные за несколько последовательных периодов времени.

Зависимость общих затрат от объема материального потока можно записать в следующем виде:

TC= FC+ AVC * Q (3. 5)

Ставку сумма переменных затрат можно определить по формуле (3. 6)

AVC=

Общая сумма переменных затрат составит:

VC= TC * Q (3. 7)

Тогда постоянные затраты определяются по формуле

FC= TC- VC (3. 8)

Использование метода наименьших квадратов хотя и усложняет процедуру расчетов, но позволяет более точно произвести распределение валовых затрат на переменные и постоянные, так как в расчетах используется исходные данные за весь период работы предприятия, входящего в логистическую систему.

Задача 3.3

На основании данных задачи 3. 1 необходимо распределить общие издержки на постоянные и переменные, используя метод наименьших квадратов.

Решение задачи (Вариант 2)

Последовательность определения коэффициентов уравнения (3. 5) и результаты расчетов представлены в таблице 3. 3.

Таблица 3. 3

Определим ставку переменных затрат в соответствии с формулой (3. 6):

AVC=2889,3/94,53=30,5 руб./т.

Общая сумма переменных затрат составит:

VC=30,5*15,25=465,125 тыс. руб.

Тогда постоянные затраты будут равны:

FC=5004,45-465,125=4539,3 тыс. руб.

В аналитической форме общие расходы на электроэнергию можно представить следующим образом:

а) по методу максимальной и минимальной точки:

ТС=4130,35+45,9*Q;

б) по графическому методу:

ТС=4250+49,5*Q;

в) по методу наименьших квадратов:

ТС=4539,3+30,5*Q.

Незначительные отклонения в величине постоянных расходов произошли из- за округления промежуточных вычислений.

Задача 4. 2

Оценить риск инвестиционных решений для двух логистических проектов А и В на основе исходных данных приведенных в таблице 4. 2

Решения задачи (вариант 2)

Исходные данные для решения примера в виде матрицы денежных потоков для инвестиций А и В (руб.) представим в виде таблицы 4. 3, а их характеристик – в виде таблицы 4. 4

Таблица 4. 2.

Исходные данные

Таблица 4. 3

Матрица денежных потоков

Таблица 4. 4

Расчет характеристик ожидаемых денежных потоков

Распределение вероятностей может быть представлено гистограммой, аналогичной приведённой на рис. 4. 5 высота отрезков прямых отражает вероятность появления денежных потоков. Для проекта А денежные потоки лежат в интервале от 300 до 900 долл. Со средним значением (или математическим ожиданием) 600 долл. Для проекта В- в интервале от 100 до 1100 долл. Со средним значением (математическим ожиданием) 600 долл.

Вероятность Вероятность

Проект А Проект В

0,5 0,5

0,4 0,4

0,3 0,3

0 300 600 900 Доход 0 100 600 1100 Доход

Рис. 4. 5. Гистограмма ожидаемых денежных потоков для проектов А и В.

На основе гистограмм построим кривые распределения доходов (рис. 4. 6).

Как видно из рисунка денежные потоки (доходы) подчиняются нормальному закону распределения. Из кривых распределения следует, что ожидаемая прибыль для проекта А меньше отличается от среднего значения ( математического ожидания) 600 руб., чем для проекта В.

Вероятность

Проект А

Проект В

100 300 600 900 1100 денежные потоки

Рис. 4. 6. Распределение денежных потоков (доходов)

Рассчитаем математическое ожидание М(х) по формуле (4. 14), дисперсию

И стандартное отклонение б для проекта А и проекте В по формуле (4. 15). Полученные данные занесем в таблицу 4. 5.

Таблица 4.5

Стандартное отклонение для проектов А и В*

Проект В оказывается более рискованным, чем проект А, поскольку стандартное отношение для проекта В (316,2руб.) больше, чем для проекта А (189,7руб.). Так как ожидаемые денежные потоки идентичны, следует предпочесть менее рискованную инвестицию – проект А (если только мы не стремимся к рискованным мероприятиям). В данном примере проекты А и В имели различные стандартные отклонения, и проект А, для которого это Значение меньше, оказался менее рискованным.

Не нашли, что искали? Воспользуйтесь поиском по сайту: