
|
|
ЗАНИМАТЕЛЬНАЯ МАТЕМАТИКА, МАТЕМАТИКА, СПОСОБЫ УМНОЖЕНИЯРАБОЧАЯ ПРОГРАММА ФАКУЛЬТАТИВА «ЗАНИМАТЕЛЬНАЯ МАТЕМАТИКА» Пояснительная записка Цель программы: формирование мотивации к изучению математики в соответствии возрастными особенностями, Задачи программы: 1. Расширение и углубление запаса знаний учащихся и формирование математической компетенции; 2. Выявление и поддержка математически одаренных детей; 4. Развитие и совершенствование мыслительных операций, психологических качеств личности (любознательности, инициативности, трудолюбия, воли) и творческого потенциала; Форма организации - факультатив Курс рассчитан на 34 часа. Занятия проводятся 1 раз в неделю. Особенности программы:Соблюдение принципов взаимосвязи между классными и внеклассными занятиями, научной углубленности, практической направленности, занимательности и индивидуального подхода к каждому ученику. В основе создания данной программы лежат: · общедидактические принципы научности, доступности, систематичности и последовательности, связи теории с практикой, сознательности и активности, наглядности, преемственности и перспективности. · принцип занимательности. Занимательность достигается главным образом путем использования материалов занимательной математики - игр, кроссвордов, загадок, логических задач, а также путем привлечения средств наглядности - картинок, слайдов, презентаций. Это удовлетворяет интеллектуальные запросы учащихся и имеет практическое значение для учащихся начальной школы. · принцип разнообразия форм и видов работы. Интерес учащихся поддерживается не только содержанием проводимых занятий, но и их разнообразием, необычностью их форм и видов, отличных от уроков, а также необычностью формулировки тем занятий, формы преподнесения материала. Основные виды деятельности учащихся: · решение занимательных задач; · участие в математической олимпиаде, международной игре «Кенгуру», «Ак Бота» · знакомство с научно-популярной литературой, связанной с математикой; · самостоятельная работа; · работа в парах, в группах; · творческие работы Предполагаемые результаты:Занятия должны помочь учащимся: · усвоить основные базовые знания по математике; её ключевые понятия; · помочь учащимся овладеть способами исследовательской деятельности; · формировать творческое мышление; · практиковаться в решении задач различного уровня сложности учащимися; · успешному выступлению на олимпиадах, играх, конкурсах.
Литература: · А.Б.Акпаева, Л.А.Лебедева, М.Ж.Мынжасарова. Занимательная математика. Алматыкытап,2015 год · А.Б.Акпаева, Л.А.Лебедева, М.Ж.Мынжасарова. Сборник задач и упражнений по математике. Алматыкытап,2015 год · Линник Р.Р. Сборник тестовых заданий по математике, Кокшетау · О.А. Ефремушкина «Школьные олимпиады для начальных классов». Ростов –на- Дону «Феникс» - 2006 · О.В.Узорова, Е.А.Нефедова. Уникальный рабочий материал по математике.Москва,2005 год · В.И.Кузнецов. Задачник по математике. Москва,1999
Интернет- ресурсы: · Портал Внеурока.ru ( http://vneuroka.ru)
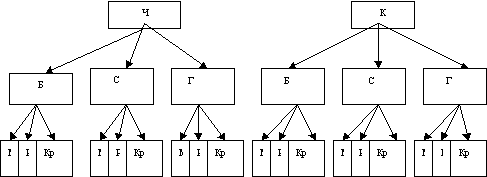
Элементы комбинаторики. Методы решения некоторых задач · Красавина Юлия Константиновна, учитель математики · Тевосова Каринэ Амбарцумовна, учитель математики Разделы: Математика Немного истории. В математике и ее приложениях часто приходится иметь дело с различного рода множествами и подмножествами: устанавливать их связь между элементами каждого, определять число множеств или их подмножеств, обладающих заданным свойством. Такие задачи приходится рассматривать при определении наиболее выгодных коммуникаций внутри города, при организации автоматической телефонной связи, работы морских портов, при выявлении связей внутри сложных молекул, генетического кода, а также в лингвистике, в автоматической системе управления, значит и в теории вероятностей, и в математической статистике со всеми их многочисленными приложениями. Поговорим об одном из разделов теории вероятности – комбинаторике. Комбинаторика - ветвь математики, изучающая комбинации и перестановки предметов. Еще комбинаторику можно понимать как перебор возможных вариантов. Комбинаторика возникла в 17 веке. Долгое время она лежала вне основного русла развития математики. ЗАДАЧИ 1. В школьной столовой на первое можно заказать борщ, солянку, грибной суп, на второе - мясо с макаронами, рыбу с картошкой, курицу с рисом, а на третье - чай и компот. Сколько различных обедов можно составить из указанных блюд? 1 способ. Перечислим возможные варианты
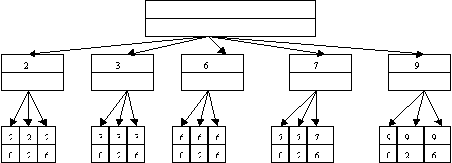
18 вариантов. 3 способ. Используя правило умножения, получаем: 3х3х2=1 2. Свете на день рождения подарили 4 плюшевых игрушки, 2 мяча и 5 кукол. Мама положила все игрушки в большую коробку. Сколькими способами Света сможет достать из коробки 1 плюшевую игрушку, 1 мяч и 1 куклу? 1 способ. Обозначим мячи - М1, М2, игрушки- И1,И2,И3, И4, куклы- К1,К2, К3, К4, К5. М1-И1-К1, М1-И1-К2, М1-И1-К3, М1-И1-К4, М1-И1-К5, Ответ: 40 вариантов. 3. Сколько четных двузначных чисел можно составить из цифр 0, 2, 3, 6, 7, 9? 1 способ. 2 способ. Дерево возможностей.
3 способ. Используя правило умножения, получаем: 5х3=15 . 4. Мисс Марпл, расследуя убийство, заметила отъезжающее от дома мистера Дэвидсона такси. Она запомнила первую цифру “2”. В городке номера машин были трехзначные и состояли из цифр 1,2,3,4 и 5. Скольких водителей, в худшем случае, ей придется опросить, чтобы найти настоящего убийцу? 1 способ. Перечислим возможные варианты номеров такси: Ответ: 25 человек. 2 способ. Используя правило умножения, получаем: 5х5=25 5. Саша, Петя, Денис, Оля, Настя часто ходят в кафе. Каждый раз, обедая там, они рассаживаются по-разному. Сколько дней друзья смогут это сделать без повторения? 1 способ. Пронумеруем стулья, на которых должен сесть каждый, и будем считать, что они рассаживаются поочередно: №1 - Саша - есть возможность выбрать из 5 вариантов (стульев) Используя правило умножения, получаем: 5х4х3х2х1=120 2 способ. Решаем, используя понятие факториала: 5!=120 6. Из учащихся пяти 11 классов нужно выбрать двоих дежурных. Сколько пар дежурных можно составить (ученики в паре не должны быть из одного класса)? 1 способ. Перечислим возможные варианты состава пары: 11А-11Б, 11А-11В, 11А-11Г, 11А-11Д, Ответ: 10 пар. 2 способ. Из пяти классов нужно выбрать 2 дежурных. 7. В 8 “а” классе лучше всех математику знают 5 учеников: Вася, Дима, Олег, Катя и Аня. На олимпиаду по математике нужно отправить пару, состоящую из 1 мальчика и 1 девочки. Сколькими способами учительница может эту пару выбрать? 1 способ. Обозначим имена детей первыми заглавными буквами. Ответ: 6 пар. 2 способ. Мальчиков 3, из них 1 можно выбрать 8. В соревнованиях по фигурному катанию принимали участие россияне, итальянцы, украинцы, немцы, китайцы и французы. Сколькими способами могут распределится места по окончании соревнований? 2 способ. Используя понятие факториала, получаем: 6!=720 9. В 9 “б” классе 6 человек (Галя, Света, Катя, Оля, Максим, Витя) учатся на все пятерки. Департамент образования премировал лучших учащихся путевками в Анапу. Но, к сожалению, путевок всего четыре. Сколько возможно вариантов выбора учеников на отдых? Обозначим первыми заглавными буквами имен учащихся. 2 способ. Из 6 человек нужно выбрать 4, число элементарных событий равно 10. Пете на день рождения подарили 7 новых дисков с играми, а Вале папа привез 9 дисков из командировки. Сколькими способами они могут обменять 4 любых диска одного на 4 диска другого? Вычислим, сколько четверок из 7 дисков можно составить у Пети: 11. Войсковое подразделение состоит из 5 офицеров, 8 сержантов и 70 рядовых. Сколькими способами можно выделить отряд из 2 офицеров, 4 сержантов и 15 рядовых? Из 5 офицеров выбрать 2 можно с помощью числа сочетаний 12. В ювелирную мастерскую привезли 6 изумрудов, 9 алмазов и 7 сапфиров. Ювелиру заказали браслет, в котором 3 изумруда, 5 алмазов и 2 сапфиров. Сколькими способами он может выбрать камни на браслет? Из 6 изумрудов 3 он может выбрать 13. На выборах победили 9 человек - Сафонов, Николаев, Петров, Кулаков, Мишин, Гусев, Володин, Афонин, Титов. Из них нужно выбрать председателя, заместителя и профорга. Сколькими способами это можно сделать? Здесь речь идет о размещениях 14. В районе построили новую школу. Из пришедших 25 человек нужно выбрать директора школы, завуча начальной школы, завуча среднего звена и завуча по воспитательной работе. Сколькими способами это можно сделать? На должность директора выбираем из 25 человек, на завуча начальной - из 24, завуча среднего звена - из 23, завуча по воспитательной работе - 22. По правилу умножения получаем: 15. В студенческом общежитии в одной комнате живут трое студентов Петя, Вася и Коля. У них есть 6 чашек, 8 блюдец и 10 чайных ложек (все принадлежности отличаются друг от друга). Сколькими способами ребята могут накрыть стол для чаепития (так, что каждый получит чашку, блюдце и ложку)? Для Пети набор можно набрать 6х8х10=480 способами, для Васи - 5х7х9=315, для Коли - 4х6х8=192. По правилу умножения получаем 16. В кабинете заведующего ювелирного магазина имеется код, состоящий из двух различных гласных букв русского алфавита, за которой следуют 3 различные цифры. Сколько вариантов придется перебрать мошеннику, чтобы раздобыть драгоценности, которые там хранятся? В русском языке 9 гласных букв - а, е, е, и, о, у, э, ю, я. Выбрать из них 2 можно 17. Сколькими способами можно составить трехцветный флаг из полос разной ширины, если имеются материи из 8 тканей? Другой способ решения. 18. В 9 классе 15 предметов. Завучу школы нужно составить расписание на субботу, если в этот день 5 уроков. Сколько различных вариантов расписания можно составить, если все уроки различные? Из 15 предметов 5 любых можно выбрать 19. В огороде у бабушки растут 3 белые, 2 алые и 4 чайных розы. Сколькими различными способами можно составить букет из трех роз разного цвета? 1 способ. Обозначим белые - Б1, Б2, Б3, алые - А1,А2, чайные - Ч1, Ч2, Ч3,Ч4 Ответ: 24 варианта. 2способ. Дерево возможностей
3 способ. Используя правило умножения, получаем: 2х3х4=24 20. К 60-летию Победы группа школьников отправилась по местам боевых действий в Смоленской области. Они планировали осуществить поход по маршруту деревни Сосновка-Быковка- Масловка- Видово. Из С в Б можно проплыть по реке или пройти пешком, из Б в М- пешком или на автобусе, из М в В - по реке, пешком или автобусе. Сколько вариантов похода есть у щкольников? 1 способ. Обозначим СБ - путь из Сосновки в Бытовку, ВГ - путь из Быковки в Масловку, МВ - путь из Масловки в Видово. 2 способ. Дерево возможностей
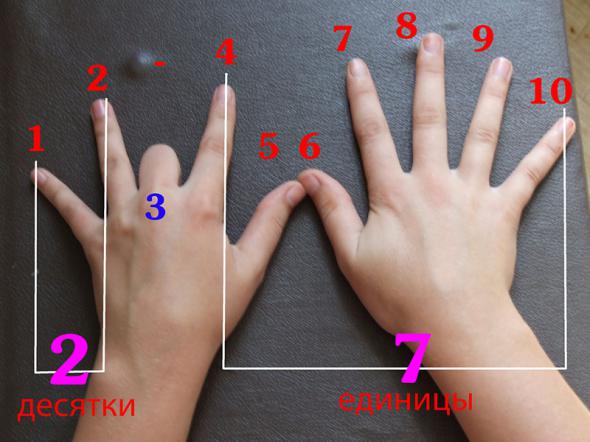
ЛИТЕРАТУРА 1) Еженедельное учебно-методическое приложение “Математика” Изд. Пресса. Москва.1999 г 2) Ю.Н.Макарычев и др. Алгебра 9. Учебник для класса с углубленным изучением математики. Изд. Мнемозина, Москва.2005 год. 3) Л.Г. Петерсон. Математика 4 класс. Изд. Баласс. Москва.1999 г. 4) Ю.Н. Тюрин и др. Теория вероятностей и статистика. МЦНМО. Москва. 2004 год. ЗАНИМАТЕЛЬНАЯ МАТЕМАТИКА, МАТЕМАТИКА, СПОСОБЫ УМНОЖЕНИЯ ХИТРАЯ ТАБЛИЦА УМНОЖЕНИЯ НА ПАЛЬЦАХ. ДЛЯ ДЕТЕЙ В жизни люди, способные вычислять в уме, смотрятся как «суперумники», хотя в этом ничего сложного нет. Калькулятор калькулятором, а считать в уме полезно! Умножение на 2 или удваивание. Удваивать довольно легко, достаточно что-то сложить с самим собой. Вначале я показал на своей левой и правой руке одновременно по одному, двум, трем, четырем, пяти пальцам – так мы получили 2, 4, 6, 8, 10. Вместе с пальцами моего ученика мы дошли до двадцати, а потом я показывал на разные штуки в комнате, и предлагал сосчитать и удвоить – число букв в плакате, число символов на циферблате часов, сосчитать число спиц на одной стороне колеса велосипеда, и проверить, сойдется ли общее число с удвоенным и так далее. Умножение на 4 и 8, 3 и 6 Когда умеешь умножать на два, это сущие пустяки. Умножить на четыре это то же, что удвоить ответ для того, что уже удвоено, например 7×4 это 7×2х2, а что 7×2 это 14 мы уже хорошо запомнили на предыдущем уроке про удваивания, так что и само 14 превратить в 28 не составит труда. Когда разобрался с четверкой, не так уж сложно разобраться и с большими числами восьмерки. По пути мы заметили, что, например, 16 это и 2×8, и 4×4. Так мы узнали, что есть числа, сплошь состоящие из двоек: 2, 4, 8, 16, 32, 64. Умножая на 3 и 6, мы выучили старый пиратский метод «дележки на три». Если сложить цифры в числе, умноженном на 3, 6 или любом другом, которое делится на тройку, то результат сложения цифр ответа всегда кратен трем. Например, 3×5 = 15, 1+5 = 6. Или 6×8 = 48, а 4+8 = 12, кратно трем. А можно и в 12 цифры сложить, получится тоже 3, так что, если так дойти до конца, то всегда получается одно из трех чисел: 3, 6 или 9. Так мы превратили это в еще одну игру. Я задавал какое-нибудь число, даже трех- или четырехзначное, и спрашивал, делится ли оно на 3. Для ответа достаточно сложить цифры, что довольно просто. Если число делилось на 3, то я спрашивал — «а на 6?» – и тогда нужно было просто посмотреть четное ли оно. А потом (в специальном случае небольших чисел из таблицы) иногда еще хотел узнать, что же получится при таком делении на 3 или 6. Это было очень веселое занятие. Умножение на 5 и 7, простые числа Мы увидели, что 60 удобно делить на 1, 2, 3, 4, 5, 6, а на 7 делить неудобно. Поэтому было самое время присмотреться к этому числу. Из умножения на семерку оставалось запомнить лишь 7×7 и 7×9. Теперь мы знали почти все, что нужно. Я объяснил, что семь просто очень гордое число – такие числа называются простые, они делятся только на 1 и на себя. Математика может быть веселой и легкой. Познакомтесь с этой симпатичной таблицей. Итак, поехали. Для начала положим свои руки на стол и мысленно пронумеруем пальчики слева направо от 1 до 10. Чтобы выполнить действие умножения, допустим 9 х 3 = ?, загибаем третий слева пальчик. Всё! Ответ готов: оставшиеся не загнутыми пальчики слева образуют количество десятков в ответе, а не загнутые справа — количество единиц. Считаем, и говорим ответ: 27!
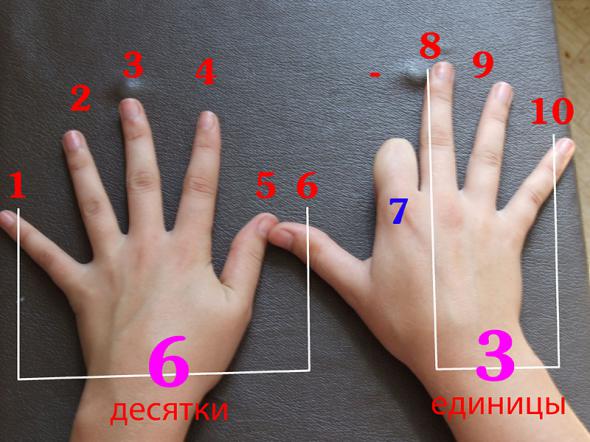
Таким образом можно получить ответ для любого числа. Вот здесь, допустим, пример 9 х 7 = 63

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
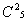 = 10
= 10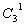 , девочек 2, из них можно 1 выбрать
, девочек 2, из них можно 1 выбрать 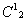 , используя правило умножения, получаем:
, используя правило умножения, получаем: = 15
= 15 =35, число четверок у Вали из 9 дисков -
=35, число четверок у Вали из 9 дисков - 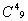 = 126
= 126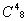 =70, из 70 рядовых 15 -
=70, из 70 рядовых 15 -  . По правилу умножения находим число выбора отряда:
. По правилу умножения находим число выбора отряда: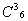 =20 способами, из 9 алмазов 5 -
=20 способами, из 9 алмазов 5 - 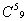 =126, из 7 сапфиров 2 -
=126, из 7 сапфиров 2 - 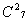 =21. По правилу умножения находим число вариантов 20х126х21=52920
=21. По правилу умножения находим число вариантов 20х126х21=52920
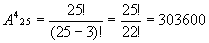
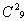 =36 способами. Из 10 цифр выбрать 3 можно
=36 способами. Из 10 цифр выбрать 3 можно 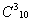 =120 способами. Применяя правило умножения, получаем:
=120 способами. Применяя правило умножения, получаем:



 На многих людей математика может наводить ужас. Этот список, возможно, улучшит общие знания о математических приемах и ускорит выполнение математических вычислений в уме.
1. Умножение на 11
Все мы знаем, что при умножении на 10 к числу добавляется 0, а знаете ли вы, что существует такой же простой способ умножения двузначного числа на 11? Вот он:
Возьмите исходное число и представьте промежуток между двумя знаками (в этом примере мы используем число 52): 5_2
Теперь сложите два числа и запишите их по середине: 5_(5+2)_2
Таким образом, ваш ответ: 572.
Если при сложении чисел в скобках получается двузначное число, просто запомните вторую цифру, а единицу прибавьте к первому числу: 9_(9+9)_9 (9+1)_8_9 10_8_9 1089 – Это срабатывает всегда.
2. Быстрое возведение в квадрат
Этот прием поможет быстро возвести в квадрат двузначное число, которое заканчивается на 5. Умножьте первую цифру саму на себя +1, а в конце допишите 25. Вот и все! 252 = (2x(2+1)) & 25 2 x 3 = 6 625
3. Умножение на 5
Большинство людей очень просто запоминает таблицу умножения на 5, но, когда приходится иметь дело с большими числами, сделать это становится сложнее, или нет? Этот прием невероятно прост.
Возьмите любое число, разделите на 2 (другими словами, поделите пополам). Если в результате получилось целое число, припишите 0 в конце. Если нет, не обращайте внимание на запятую и в конце добавьте 5. Это срабатывает всегда: 2682 x 5 = (2682 / 2) & 5 или 0 2682 / 2 = 1341 (целое число, поэтому добавьте 0) 13410
Давайте попробуем другой пример: 5887 x 5 2943,5 (дробное число (пропустите запятую, добавьте 5) 29435
На многих людей математика может наводить ужас. Этот список, возможно, улучшит общие знания о математических приемах и ускорит выполнение математических вычислений в уме.
1. Умножение на 11
Все мы знаем, что при умножении на 10 к числу добавляется 0, а знаете ли вы, что существует такой же простой способ умножения двузначного числа на 11? Вот он:
Возьмите исходное число и представьте промежуток между двумя знаками (в этом примере мы используем число 52): 5_2
Теперь сложите два числа и запишите их по середине: 5_(5+2)_2
Таким образом, ваш ответ: 572.
Если при сложении чисел в скобках получается двузначное число, просто запомните вторую цифру, а единицу прибавьте к первому числу: 9_(9+9)_9 (9+1)_8_9 10_8_9 1089 – Это срабатывает всегда.
2. Быстрое возведение в квадрат
Этот прием поможет быстро возвести в квадрат двузначное число, которое заканчивается на 5. Умножьте первую цифру саму на себя +1, а в конце допишите 25. Вот и все! 252 = (2x(2+1)) & 25 2 x 3 = 6 625
3. Умножение на 5
Большинство людей очень просто запоминает таблицу умножения на 5, но, когда приходится иметь дело с большими числами, сделать это становится сложнее, или нет? Этот прием невероятно прост.
Возьмите любое число, разделите на 2 (другими словами, поделите пополам). Если в результате получилось целое число, припишите 0 в конце. Если нет, не обращайте внимание на запятую и в конце добавьте 5. Это срабатывает всегда: 2682 x 5 = (2682 / 2) & 5 или 0 2682 / 2 = 1341 (целое число, поэтому добавьте 0) 13410
Давайте попробуем другой пример: 5887 x 5 2943,5 (дробное число (пропустите запятую, добавьте 5) 29435
 4. Умножение на 9
Это просто. Чтобы умножить любое число от 1 до 9 на 9, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например 9х3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9х3 – это 2), затем посчитайте после загнутого пальца (в нашем случае – 7). Ответ – 27.
5. Умножение на 4
Это очень простой прием, хотя очевиден лишь для некоторых. Хитрость в том, что нужно просто умножить на 2, а затем опять умножить на 2: 58 x 4 = (58 x 2) + (58 x 2) = (116) + (116) = 232
6. Подсчет чаевых
Если вам нужно оставить 15% чаевых, есть простой способ сделать это. Высчитайте 10% (разделите число на 10), а потом добавьте получившееся число к его половине и получите ответ: 15% от $25 = (10% от 25) + ((10% от 25) / 2) $2.50 + $1.25 = $3.75
7. Сложное умножение
Если вам нужно умножать большие числа, причем одно из них — четное, вы можете просто перегруппировать их, чтобы получить ответ: 32 x 125 все равно, что: 16 x 250 все равно, что: 8 x 500 все равно, что: 4 x 1000 = 4,000
4. Умножение на 9
Это просто. Чтобы умножить любое число от 1 до 9 на 9, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например 9х3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9х3 – это 2), затем посчитайте после загнутого пальца (в нашем случае – 7). Ответ – 27.
5. Умножение на 4
Это очень простой прием, хотя очевиден лишь для некоторых. Хитрость в том, что нужно просто умножить на 2, а затем опять умножить на 2: 58 x 4 = (58 x 2) + (58 x 2) = (116) + (116) = 232
6. Подсчет чаевых
Если вам нужно оставить 15% чаевых, есть простой способ сделать это. Высчитайте 10% (разделите число на 10), а потом добавьте получившееся число к его половине и получите ответ: 15% от $25 = (10% от 25) + ((10% от 25) / 2) $2.50 + $1.25 = $3.75
7. Сложное умножение
Если вам нужно умножать большие числа, причем одно из них — четное, вы можете просто перегруппировать их, чтобы получить ответ: 32 x 125 все равно, что: 16 x 250 все равно, что: 8 x 500 все равно, что: 4 x 1000 = 4,000
 8. Деление на 5
На самом деле делить большие числа на 5 очень просто. Все, что нужно, - просто умножить на 2 и перенести запятую: 195 / 5 Шаг1: 195 * 2 = 390 Шаг2: Переносим запятую: 39,0 или просто 39.
2978 / 5 Шаг1: 2978 * 2 = 5956 Шаг2: 595,6
9. Вычитание из 1000
Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом: Отнимите от 9 все цифры, кроме последней. А последнюю цифру отнимите от 10: 1000 -648 Шаг1: от 9 отнимите 6 = 3 Шаг2: от 9 отнимите 4 = 5 Шаг3: от 10 отнимите 8 = 2 Ответ: 352
10. Систематизированные правила умножения
· Умножение на 5: Умножьте на 10 и разделите на 2.
· Умножение на 6: Иногда проще умножить на 3, а потом на 2.
· Умножение на 9: Умножьте на 10 и отнимите исходное число.
· Умножение на 12: Умножьте на 10 и дважды прибавьте исходное число.
· Умножение на 13: Умножьте на 3 и 10 раз прибавьте исходное число.
· Умножение на 14: Умножьте на 7, а затем — на 2.
· Умножение на 15: Умножьте на 10 и 5 раз прибавьте исходное число, как в предыдущем примере.
· Умножение на 16: Если хотите, 4 раза умножьте на 2. Или умножить на 8, а потом на 2.
· Умножение на 17: Умножьте на 7 и 10 раз прибавьте исходное число.
· Умножение на 18: Умножьте на 20 и дважды отнимите исходное число.
· Умножение на 19: Умножьте на 20 и отнимите исходное число.
· Умножение на 24: Умножьте на 8, а потом на 3.
· Умножение на 27: Умножьте на 30 и 3 раза отнимите исходное число.
· Умножение на 45: Умножьте на 50 и 5 раз отнимите исходное число.
· Умножение на 90: Умножьте на 9 и припишите 0.
· Умножение на 98: Умножьте на 100 и дважды отнимите исходное число.
· Умножение на 99: Умножьте на 100 и отнимите исходное число.
Бонус: Проценты
Yanni в 23-м комментарии дал отличный совет, как высчитать проценты. Поэтому я взял на себя смелость повторить его здесь:
Вычислить 7% от 300. Кажется сложным?
Проценты: Сперва нужно понять значение слова «Процент» (Percent). Первая часть слова — ПРО (PER) , как 10 пунктов на страницу сайта listverse. PER = ДЛЯ КАЖДОГО. Вторая часть — ЦЕНТ (CENT), как 100. Например, СТОлетие = 100 лет. 100 ЦЕНТов в 1 долларе и так далее. Итак, ПРОЦЕНТ = ДЛЯ КАЖДОЙ СОТНИ.
Итак, получается, что 7% от 100 будет 7. (7 для каждой сотни, только одной сотни). 8% от 100 = 8. 35,73% от 100 = 35,73
Но как это может быть полезным?? Вернемся к задачке 7% от 300. 7% от первой сотни равно 7. 7%, от второй сотни — то же 7, и 7% от третьей сотни - все те же 7. Итак, 7 + 7 + 7 = 21. Если 8% от 100 = 8, то 8% от 50 = 4 (половина от 8).
Дробите каждое число, если нужно вычислить проценты из 100, если же число меньше 100, просто перенесите запятую влево.
ПРИМЕРЫ: 8%200 = ? 8 + 8 = 16. 8%250 = ? 8 + 8 + 4 = 20, 8%25 = 2,0 (Передвигаем запятую влево). 15%300 = 15+15+15 =45, 15%350 = 15+15+15+7,5 = 52,5
Также полезно знать, что вы всегда можете поменять числа местами: 3% от 100 — то же самое, что 100% от 3. 35% от 8 — то же самое, что и 8% от 35
8. Деление на 5
На самом деле делить большие числа на 5 очень просто. Все, что нужно, - просто умножить на 2 и перенести запятую: 195 / 5 Шаг1: 195 * 2 = 390 Шаг2: Переносим запятую: 39,0 или просто 39.
2978 / 5 Шаг1: 2978 * 2 = 5956 Шаг2: 595,6
9. Вычитание из 1000
Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом: Отнимите от 9 все цифры, кроме последней. А последнюю цифру отнимите от 10: 1000 -648 Шаг1: от 9 отнимите 6 = 3 Шаг2: от 9 отнимите 4 = 5 Шаг3: от 10 отнимите 8 = 2 Ответ: 352
10. Систематизированные правила умножения
· Умножение на 5: Умножьте на 10 и разделите на 2.
· Умножение на 6: Иногда проще умножить на 3, а потом на 2.
· Умножение на 9: Умножьте на 10 и отнимите исходное число.
· Умножение на 12: Умножьте на 10 и дважды прибавьте исходное число.
· Умножение на 13: Умножьте на 3 и 10 раз прибавьте исходное число.
· Умножение на 14: Умножьте на 7, а затем — на 2.
· Умножение на 15: Умножьте на 10 и 5 раз прибавьте исходное число, как в предыдущем примере.
· Умножение на 16: Если хотите, 4 раза умножьте на 2. Или умножить на 8, а потом на 2.
· Умножение на 17: Умножьте на 7 и 10 раз прибавьте исходное число.
· Умножение на 18: Умножьте на 20 и дважды отнимите исходное число.
· Умножение на 19: Умножьте на 20 и отнимите исходное число.
· Умножение на 24: Умножьте на 8, а потом на 3.
· Умножение на 27: Умножьте на 30 и 3 раза отнимите исходное число.
· Умножение на 45: Умножьте на 50 и 5 раз отнимите исходное число.
· Умножение на 90: Умножьте на 9 и припишите 0.
· Умножение на 98: Умножьте на 100 и дважды отнимите исходное число.
· Умножение на 99: Умножьте на 100 и отнимите исходное число.
Бонус: Проценты
Yanni в 23-м комментарии дал отличный совет, как высчитать проценты. Поэтому я взял на себя смелость повторить его здесь:
Вычислить 7% от 300. Кажется сложным?
Проценты: Сперва нужно понять значение слова «Процент» (Percent). Первая часть слова — ПРО (PER) , как 10 пунктов на страницу сайта listverse. PER = ДЛЯ КАЖДОГО. Вторая часть — ЦЕНТ (CENT), как 100. Например, СТОлетие = 100 лет. 100 ЦЕНТов в 1 долларе и так далее. Итак, ПРОЦЕНТ = ДЛЯ КАЖДОЙ СОТНИ.
Итак, получается, что 7% от 100 будет 7. (7 для каждой сотни, только одной сотни). 8% от 100 = 8. 35,73% от 100 = 35,73
Но как это может быть полезным?? Вернемся к задачке 7% от 300. 7% от первой сотни равно 7. 7%, от второй сотни — то же 7, и 7% от третьей сотни - все те же 7. Итак, 7 + 7 + 7 = 21. Если 8% от 100 = 8, то 8% от 50 = 4 (половина от 8).
Дробите каждое число, если нужно вычислить проценты из 100, если же число меньше 100, просто перенесите запятую влево.
ПРИМЕРЫ: 8%200 = ? 8 + 8 = 16. 8%250 = ? 8 + 8 + 4 = 20, 8%25 = 2,0 (Передвигаем запятую влево). 15%300 = 15+15+15 =45, 15%350 = 15+15+15+7,5 = 52,5
Также полезно знать, что вы всегда можете поменять числа местами: 3% от 100 — то же самое, что 100% от 3. 35% от 8 — то же самое, что и 8% от 35