
|
|
Метод цепных подстановок.Практическое занятие № 0 (15) к разделу 3 Комплексный экономический анализ Экономико-математические методы экономического анализа. Метод дифференциального исчисления. Теоретической основой для количественной оценки роли отдельного фактора в динамике обобщающего показателя является метод дифференциального исчисления, при применении которого предполагается, что общее приращение функции (обобщающего, результирующего показателя) раскладывается на составляющие и значение каждого из них определяется как произведение соответствующей частной производной на приращение переменной, по которой вычислена данная производная. Пусть задана функция
Влияние факторов Х и У на изменение показателя Z определяется как:
а их сумма представляет собой главную, линейную относительно приращения факторов часть приращения дифференцируемой функции. Следует отметить, что остаток
Интегральный метод оценки факторных влияний. Интегральный метод факторного анализа является дальнейшим логическим развитием метода дробления приращения факторных признаков и основывается на суммировании приращений функции, определенной как частная производная, умноженная на приращение аргумента на бесконечно малом промежутке. При этом должны соблюдаться следующие условия: 1) непрерывная дифференцируемость функции, где в качестве аргумента используется экономический показатель; 2) функция между начальной и конечной точками элементарного периода изменятся по гладкой прямой; 3) постоянства соотношения скоростей изменения факторов. Пусть задана функция изменения результирующего показателя от факторов
где xi - значения факторов (i = 1,2,3,...,m); y - значение результирующего показателя. Факторы изменяются во времени и известны значения каждого фактора в n точках m-го пространства
…………….
Точки М1 и Мn соответствуют значениям факторов на начало и конец анализируемого периода соответственно. Можно показать, что изменение функции на рассматриваемом интервале определяется выражением
где i=1,2,3,…,n-1; у=1,2,3,…,m. Вычислив все интегралы, получим матрицу:
Каждый элемент этой матрицы характеризует вклад соответствующего фактора в изменение результирующего показателя за i-ый период. Сумма всех элементов матрицы составляет полное приращение результирующего показателя. Интегральный метод целесообразно использовать, если отсутствуют данные об изменениях факторов внутри анализируемого периода или когда от них можно абстрагироваться, например, в статистических задачах, характеризующихся постоянством положения факторов по отношению к одному фактору и постоянством условий анализа измеряемых факторов независимо от нахождения их в модели факторной системы. Важной особенностью интегрального метода является то, что оно дает общий подход к решению задач самого различного вида независимо от количества элементов, входящих в модель факторной системы, и формы связей между ними. Метод цепных подстановок. Метод заключается в вычислении ряда промежуточных значений обобщающего показателя путем последовательной замены базисных значений факторов на фактические. Разность двух промежуточных значений обобщающего показателя в цепи подстановок равна изменению обобщающего показателя, вызванного изменением соответствующего фактора. В общем виде имеет следующую систему расчетов по методу цепных подстановок:
………………
Общее абсолютное отклонение обобщающего показателя определяется формулой:
Общее отклонение обобщающего показателя раскладывается на факторы: - за счет изменения фактора А:
- за счет изменения фактора В:
и так далее. Недостатком метода цепных подстановок, как и индексного метода, являются: - результаты расчетов зависят от последовательности замены факторов; - активная роль в изменении обобщающего показателя необоснованно часто приписывается влиянию изменения качественного показателя. Обычно весь прирост обобщающего показателя за счет совместного изменения факторов приписывается влиянию качественного фактора. Поэтому задача точного определения роли каждого фактора в изменении обобщающего показателя обычным методом цепных подстановок не решается. Поиск путей совершенствования точного определения роли отдельных факторов ведется с двух позиций: - экономического обоснования определенной последовательности подстановок путем исследования сущности хозяйственных процессов и связей экономических факторов, при котором порядок расчетов определяется не порядком расположения показателей в расчетной формуле, а их конкретным содержанием с выделением количественных и качественных факторов; - нахождением рациональной вычислительной процедуры (метода факторного анализа), при которой устраняются условности и допущения, и достигается получение однозначного результата влияния факторов. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . Если функция дифференцируема, то ее приращение можно определить как:
. Если функция дифференцируема, то ее приращение можно определить как: .
. ;
;  ,
, мал при относительно малых изменениях факторов, но его значение может существенно отличаться от нуля при больших изменениях факторов. Так как этот метод дает однозначное разложение влияния факторов на изменение результирующего показателя, то это разложение может привести к значительным ошибкам в оценке влияния факторов при исключении из рассмотрения остаточного члена, значение которого равно произведению изменений значений факторов
мал при относительно малых изменениях факторов, но его значение может существенно отличаться от нуля при больших изменениях факторов. Так как этот метод дает однозначное разложение влияния факторов на изменение результирующего показателя, то это разложение может привести к значительным ошибкам в оценке влияния факторов при исключении из рассмотрения остаточного члена, значение которого равно произведению изменений значений факторов .
. ,
, ,
, ,
, .
. ,
,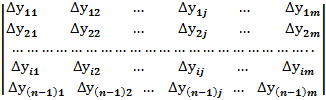 .
. ,
, ,
,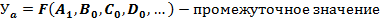 ,
, ,
, ,
, .
. .
. ,
, ,
,