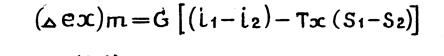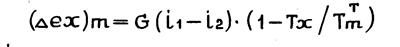Основные определения и соотношения эксергетического метода анализа

При анализе термодинамических систем необходимо учитывать на ряду с первым, второй закон термодинамики. Согласно второму закону термодинамики любой теплопроцесс характеризуется ростом энтропии системы. Следовательно, приращение энтропии системы может явиться абсолютным критерием термодинамического совершенства анализируемого теплопроцесса. Сумма приращений энтропии по всем теплоиспользующим элементам будет определять подвод энергии от внешнего источника. Приращение энтропии в локальном теплоиспользующем элементе пропорционально перерасходу химической энергии топлива, например, в котле ТЭЦ или другой организованной формы подведенной энергии. Задачей термодинамического анализа является определение перерасхода топлива в каждом локальном теплопроцессе сложной термотехнологической системы, определение КПД этого локального теплопроцесса и его связь с КПД системы.

Метод термодинамического анализа, учитывающий при анализе технологических систем как первый, так и второй закон термодинамики называется эксергетическим.

В процессе энергетического взаимодействия потоков друг с другом и с окружающей средой имеет место передача энергии материальных потоков с наинизшей температурой в системе окружающей среде. Действительно, согласно второму закону термодинамики эта энергия не может быть передана остальным рабочим телам с большей температурой, т. е. является бесполезной в данной системе и переходит в окружающую среду.

Эксергия теплового потока Еq при температуре Т определяется количеством работы, которое может быть получено или должно быть затрачено в обратимом процессе переноса энтропии, характеризующей данный тепловой поток, на уровень температуры окружающей среды.

Эта термодинамическая функция характеризует не энергию теплового потока, а его максимально возможную работу, которую этот поток может совершить вне рассматриваемой системы. Следует подчеркнуть, что возможная работа теплового потока не является материальной величиной, поэтому для нее закон сохранения энергии не справедлив. Однако учет потерь от необратимости процессов (эксергетических потерь) позволяет составлять ее баланс и, следовательно, открывает возможность определения эксергетического КПД.

Математическое выражение для эксергии теплового потока в условиях изобарического процесса имеет вид

Выразим приращение энтропии через среднетермодинамическую температуру потока по формуле, тогда

где i₁, S₁, ix, Sx, ex - удельная энтальпия, энтропия, эксергия потока при заданных параметрах и параметрах окружающей среды;

Т^Т - среднетермодинамическая температура потока;

Тх – температура холодильника (окружающая среда).

Одним из основных параметров в расчетах по определению эксергетического КПД теплопередачи является среднетермодинамическая температура нагрева (охлаждения) материальных потоков в процессе их энергетического взаимодействия. Среднетермодинамическая температура (по определению) равна отношению изменения (приращения) энтальпии нагреваемого (охлаждаемого) потока к соответствующему приращению энтропии этого потока.

В большинстве практических случаев при термодинамическом анализе тепловых схем технологических процессов среднетермодинамические температуры отдельных потоков могут быть выражены через их истинные температуры следующими приближенными формулами:

для процессов без фазовых превращений

для процессов при фазовом переходе первого рода (конденсация пара)

где Тн, Тк — температуры потока в начале и конце теплового процесса; Т s— температура фазового перехода.

Для анализа термодинамической системы удобно пользоваться приращением эксергии, полученным при термическом взаимодействии материальных потоков.

или

где i₁, S₁, i₂, S₂, - энтальпия и энтропия подвода и отвода энергии от материальных потоков в анализируемом блоке системы;

G – массовый расход потока; Тm^T - среднетермодинамическая температура потока (отвода) теплового потока в m – ом блоке термодинамической системы. Абсолютная оценка термодинамического совершенства выражается через эксергетические потери.

Эксергетические потери можно получить вычитанием всех входящих и выходящих в узел эксергий.

.

В качестве относительной характеристики термодинамического совершенства процесса выступает эксергетический КПД. Составленный на основе классических законов термодинамики (первого и второго), эксергетический к.п.д. характеризует степень необратимости процессов. Определение эксергетичеоких к.п.д. теплоиспользующих элементов системы позволяет выявить процессы, характеризующие большой необратимостью, наметить пути по уменьшению или ликвидации этой необратимости.

Эксергетический к.п.д. определяется как отношение воспринятой в теплопроцессе пригодной для дальнейшего технического использования энергии к подводимой, при годной для технического использования энергии т.е. как отношение приращения эксергий.

Эксергетический к.п.д. теплообменного аппарата можно выразить

где Δех_н , Δех⁰ - приращение эксергии нагреваемого и охлаждаемого потока при энергетическом взаимодействии;

Тт, Тт^I – среднетермодинамическая температура нагреваемого и охлаждаемого потока.

В теплообменниках рекуперативного типа при определении эксергетического к. п. д. определение приращения эксергии нагреваемых и охлаждаемых потоков не представляет труда.

Эксергетический КПД процесса в рекуперативном теплообменнике.

Пример14. Определить эксергетический КПД и эксергетические потери для парового калорифера вторичного подогрева воздуха в кондиционере для холодного периода года . Пусть воздух с расходом G = 20000 кг / час нагревается в калорифере от tн = 16 ⁰C до tк = 19 ⁰C паром при температуре tп = 100 ⁰C. Теплоёмкость воздуха Св = 0,92 кДж / кг∙ град. Тх = 245 К.

Процесс адиабатический (без отвода теплоты в окружающую среду).

Тепловой баланс калорифера

Qо = Qн =G ∙ Св ∙ (tк - tн) = 20000 ∙ 0,92 ∙ (19 - 16) = 55308 кДж / час

Эксергетический баланс калорифера

Переданная эксергия водяным паром в калорифере

ΔЕо = Qо ∙ (1 – Тх / То ) = 55308 ∙ (1 – 245 / 373) = 18980 кДж / час,

где То - среднетермодинамическая температура конденсации водяного пара То = tп = 373 К

Воспринятая эксергия воздухом в калорифере

ΔЕн = Qн ∙ (1 – Тх / Тн ) = 55308 ∙ (1 – 245 / 290,5 ) =8663 кДж / час, где

Тн - среднетермодинамическая температура нагрева воздуха в калорифере

Тн = [(tк + tн) / 2] + 273 = 290,5 К

Эксергетический КПД калорифера

η = ΔЕн / ΔЕо =( 8663 / 18980) ∙ 100 = 45,6 %

Эксергетические потери в паровом калорифере

П = ΔЕо - ΔЕн = 18980 – 8663 = 10317 кДж / час.

Термодинамический анализ процесса в калорифере показывает, что он характеризуется низким эксергетическим КПД и большими эксергетическими потерями. Одним из возможных вариантов для повышения степени термодинамического совершенства процесса в калорифере - замена теплоносителя на воду или на газообразный теплоноситель. Не смотря на низкий эксергетический КПД такой процесс может быть экономически целесообразен, например, в случае использования в качестве теплоносителя отработанного водяного пара, который в альтернативном варианте отводится в окружающую среду . Некоторое затруднение вызывает определение приращения эксергии в процессах, осложненных массообменом. Можно привести тепловой процесс с массообменом к процессу в рекуперативном теплообменнике и идеальном смесителе (разделителе), которые работают последовательно. Эта условная схема (при сохранении материальных и энергетических балансов) позволяет относительно просто рассчитать приращения эксергий материальных потоков в тепловом процессе, осложненном массообменом.

Рассмотрим процессы в типичных теплоиспользующих установках систем вентиляции и кондиционирования.

Эксергетический КПД процесса в теплообменнике смешения.

Пример 15.в условиях примера 13 пусть в теплообменнике смешения нагревается воздух (рис.5) с параметрами в точке 1 воздухом с параметрами в точке 2. На рис.5 приняты следующие обозначения: для точки 1 - G₁, i₁ Т₁ — соответственно расход, удельная энтальпия, и температура нагреваемого воздуха на входе в теплообменник; для точки 2 - G₂, i₂, Т₂ — расход, удельная энтальпия, температура воздуха на входе в теплообменник; G₃, i₃ ,Т₃ - расход, удельная энтальпия, температура потока воздуха на выходе из теплообменника смешения. Для приведения рассматриваемого процесса теплообмена (рис. 1 - а) к процессу в рекуперативном (поверхностном) теплообменнике условно разобьем выходной (нагретый) поток (рис.1 - 1 б) на два: один по массе, равной нагреваемому потоку, другой - по массе, равной охлаждаемому. При этом для обоих потоков температура воздуха на выходе из теплообменника смешения Т₃ - idem. Процесс в теплообменнике адиабатический.Численные величины взаимодействующих потоков при принятых обозначениях:

G₁ = 1000 кг / час, i₁ = 41 кДж / кг, Т₁ = 295 К;

G₂ = 800 кг / час, i₂ =68 кДж / кг, Т₂ = 301 К;

G₃ = 1800 кг / час, i₃ = 53 кДж / кг, Т₃ = 297.7 К.

Рис. 5. Тепловые схемы теплообменника смешения:

а - структурная; б — эквивалентная

Тепловой баланс теплообменника смешения

Qн =G₁ ∙ (i₃ - i₁) = 1000 ∙ (53,0 - 41,0) = 12000 кДж / час

Qо = G₁ ∙ (i₂ - i₃) = 800 ∙ (68 – 53) = 12000 кДж / час

Эксергетический баланс теплообменника смешения

Переданная эксергия горячим воздухом в теплообменнике смешения

ΔЕо = Qо ∙ (1 – Тх / То ) = 12000 ∙ (1 – 273 / 299,35) = 1056,3 кДж / час,

где То - среднетермодинамическая температура охлаждения воздуха от температуры Т₂ до температуры Т₃

То = (Т₂ + Т ₃) / 2 = (301 + 297,7) /2 = 299,35 К

Воспринятая эксергия воздухом в теплообменнике смешения

ΔЕн = Qн ∙ (1 – Тх / Тн ) = 12000 ∙ (1 – 273 / 296,35 ) = 945,5 кДж / час, где

Тн - среднетермодинамическая температура нагрева воздуха в теплообменнике смешения

Тн = (T₁ + T₃) / 2 = ( 295 + 297,7) / 2 = 296,35 К

Эксергетический КПД теплообменника смешения

η = ΔЕн / ΔЕо =( 945,5/ 1056,3 ) ∙ 100 = 89,5 %

Эксергетические потери в теплообменнике смешения

П = ΔЕо - ΔЕн = 1056,3 – 945,5 =1108 кДж / час.

Анализ теплопроцесса в теплообменнике смешения показывает, что эксергетический КПД процесса достаточно высок (89,5%).

Эксергетический КПД процесса в адиабатическом самоиспарителе.

Другим типичным теплоиспользующим элементом, нашедшим применение в схемах регенерации теплоты является адиабатический самоиспаритель (рис. 6).

Процесс в этом элементе относится к процессу дросселирования перегретого раствора с внутренним энергообменом. Для приведения теплопроцесса

(рис.6 а) к процессу в рекуперативном теплообменнике разобьем (условно) выходящий поток на два: один по массе равен нагреваемому потоку (пару), другой - охлаждаемому.

К. П. Д. такого процесса

где Т_Т, Т_Т ¹ - среднетермодинамическая температура нагрева воды при превращении ее в водяной пар и охлаждения нагретого потока.

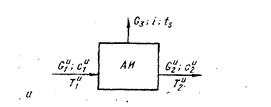
Рис. 6. Тепловые схемы адиабатического самоиспарителя:

а — структурная; б - эквивалентная .

а/и — адиабатический испаритель; т/о — рекуперативный теплообменник; G₁^и ,с₁^и ,Т₁^и — соответственно расход, удельная теплоемкость и температура перегретого раствора на входе в испаритель; G₂^и ,с₂^и ,Т₂^и — то же, на выходе из испарителя; G₃^и , i, Ts - _соответственно расход, удельная энтальпия и температура пара вскипания.

Пример 16.Рассмотрим (рис. 6) процесс в адиабатическом самоиспарителе (в водоотделителе) третьей ступени сушильной части бумагоделательной машины.

Численные величины взаимодействующих потоков при принятых обозначениях:

G₁^И = 8480 кг / час, С₁^И = 4.19 кДж / кг ∙ град, Т₁^И = 404 К;

G₂ ^И = 8338 кг / час, С₂^И = 4.19 кДж / кг ∙ град, Т₁^И = 404 К;

G₃ ^И = 142 кг / час Св = 4.19 кДж / кг ∙ град, Т₁^И = 404 К;

G₃ ^И = 142 кг / час i = 2757,6 кДж / кг, ts = 395 К

G₂^И = 8338 кг / час, С₂^И = 4.19 кДж / кг ∙ град, Т2^И = ts = 395 К

G₃ ^И = 141,9 кг / час i = 2757,6 кДж / кг, ts = 395 К

Тепловой баланс адиабатического самоиспарителя

Qо = Qн =G₂ ∙ С₂ ∙ (T₁^И - T₂^И) = 8338 ∙ 4,19 ∙ (404 - 395) = 314426 кДж / час

Эксергетический баланс адиабатического самоиспарителя

Переданная эксергия перегретой водой при ее фазовом превращении в самоиспарителе

ΔЕо = Qо ∙ (1 – Тх / То ) = 314426 ∙ (1 – 300 / 399,5 ) = 78311 кДж / час,

где То - среднетермодинамическая температура охлаждения перегретой воды

(T₁^И + T₂^И ) / 2 = 399,5 К

Воспринятая эксергия при фазовом переходе части перегретого раствора в водяной пар

ΔЕн = Qн ∙ (1 – Тх / Тн ) = 314426 ∙ (1 – 300 / 395 ) = 75621 кДж / час, где

Тн - среднетермодинамическая температура фазового перехода (температура водяного пара)

Тн = ts = 395 К

Эксергетический КПД теплообменника смешения

η = ΔЕн / ΔЕо =( 75621 / 78311 ) ∙ 100 = 96,6 %

Эксергетические потери в теплообменнике смешения

П = ΔЕо - ΔЕн = 78311 – 75621 = 1690 кДж / час.

Термодинамический анализ теплопроцесса в адиабатическом самоиспарителе показывает, что степень термодинамического совершенства этого процесса очень высока. Эксергетический КПД равен 96,6%, что свидетельствует о том, что практически все возможности по совершенствованию процесса исчерпаны.

Библиографический список

1. Альтшуль А.Д. Гидравлические сопротивления. М.: Недра, 1982.

Бельский А.П., Лотвинов М.Д. Вентиляция бумагоделательных машин. М.: Лесная промышленность, 1990.

2. Голубков Б.Н., Пятачков Б.И., РомановаТ.М. Кондиционирование воздуха, отопление и вентиляция. М.: Энергоиздат, 1982.

3. Голубков Б.Н., Романова Т.М., Гусев В.А. Проектирование и эксплуатация установок кондиционирования воздуха и отопления. М.: Энергоатомиздат, 1988.

4. Левитан Б.М. Вентиляция на предприятиях целлюлозно-бумажной промышленности. Л.: Лесная промышленность, 1972.

5. Мурзич А.Ф., Чайка М.Н. Системы вентиляции и кондиционирования воздуха: Учебное пособие / ГОУ ВПО СПб ГТУ РП. СПб., 2004.92 с. ил.40.

6. Мурзич А.Ф. Энергетические системы обеспечения жизнедеятельности человека. Методические указания по выполнению контрольной работы для студентов заочной формы обучения. / ГОУ ВПО СПб ГТУ РП. СПб., 2001.45 с.

7. Сребницкий Б.М. Примеры расчета систем кондиционирования воздуха. Киев, «Будiвельник», 1970, 158с.

8. Строительные нормы и правила. Отопление, вентиляция и кондиционирование воздуха. СНиП. М.: Стройиздат, 1994.

Не нашли, что искали? Воспользуйтесь поиском по сайту: