
|
|
Элементы теории разностных системУРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ Ранее мы рассматривали обыкновенные дифференциальные уравнения. Их решения зависят от одной переменной. Во многих практических задачах искомые функции зависят от нескольких переменных, и описывающие такие задачи уравнения могут содержать частные производные искомых функций. Они называются уравнениям с частными производными. Полная математическая постановка задачи наряду с дифференциальным уравнениями содержит также некоторые дополнительные условия. Если решение ищется в ограниченной области, то задаются условия на границе, называемые граничными (краевыми) условиями. Такие задачи называются краевыми задачами для уравнений с частными производными. Если одной из независимых переменных в рассматриваемой задаче является время t, то задаются некоторые условия в начальный момент t0, называемые начальными условиями. Задача, которая состоит в решении уравнения при заданных начальных условиях, называется задачей Коши для уравнения с частными производными. При этом задача решается в неограниченном пространстве и граничные условия не задаются. Задачи, при формулировке которых ставятся граничные и начальные условия, называются нестационарными (или смешанными) краевыми задачами. Получающиеся при этом решения меняются с течением времени. В дальнейшем будем рассматривать лишь корректно поставленные задачи, т.е. задачи, решение которых существует и единственно в некотором классе начальных и граничных условий и непрерывно зависит от как от этих условий, так и от коэффициентов уравнений. Решение простейших задач для уравнений с частными производными в ряде случаев может быть проведено аналитическими методами. Однако основным классом применяемых методов, являются численные. Среди численных методов широко распространенными являются разностные методы. Как и в случае ОДУ они основаны на введении некоторой разностной сетки в рассматриваемой области. Значения производных, начальные и граничные условия выражаются через значения функций в узлах сетки, в результате чего получается система алгебраических уравнений, называемых разностной схемой. Решая эту систему уравнений, можно найти в узлах сетки значения сеточных функций, которые приближенно считают равными значениям искомых функций. Мы будем рассматривать достаточно узкий круг задач для уравнений первого и второго порядков, линейных относительно производных. В случае двух независимых переменных эти уравнения можно записать в следующем виде:
Здесь Существуют различные виды уравнений в зависимости от соотношения между коэффициентами. 1) При a = b = c = f = 0, d¹ 0, с ¹ 0 получается уравнение первого порядка следующего вида
называемое уравнением переноса. На практике в этом уравнении одной из переменных может быть время. Тогда его называют также эволюционным уравнением. 2) Если хотя бы один из коэффициентов a, b отличен от нуля, то является уравнением второго порядка. В зависимости от знака дискриминанта Приведем некоторые примеры, которые мы будем рассматривать в дальнейшем: волновое уравнение (гиперболическое)
eравнение теплопроводности или диффузии (параболическое)
уравнение Лапласа (эллиптическое)
Если правая часть уравнения (5) отлична от нуля, то оно называется уравнением Пуассона.
Уравнение ФПК относится к уравнениям параболического вида
a=0.5; b = 0; c = 0; d =1. Таким образом D = 0 – параболическое уравнение.
Уравнение ФПК – линейное дифференциальное уравнение в частных производных параболического типа и к нему применимы методы решений, разработанные в математической физике. Суть численных методов сводится к замене дифференциального уравнения его конечно-разностным аналогом, например:
где i и j – номер расчетного шага времени и расхода воды соответственно (рис. 3.6 а). Граничными условиями могут быть, например, условия поглощения
 и и  . .
или более сжато
где
Левое граничное условие аппроксимируется так:
или
При j = 0
Подставив (3.28) в (3.27), получим:
Сравнивая (3.28) и (3.29), получаем рекуррентные формулы для расчета
Значения Зная Численно реализовать уравнения для моментов легко, если они решаются последовательно. Для нелинейной функции 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (1)
(1) - искомая функция. Коэффициенты a, b, c, d, e, f и правая часть g могут зависеть от переменных x, y и искомой функции u. В связи с этим уравнение может быть: 1) с постоянными коэффициентами; б) линейным, если g линейно зависит от u, а коэффициенты зависят только от x, y; в) квазилинейным, если коэффициенты зависят от u. Уравнение (1) – это самый общий вид.
- искомая функция. Коэффициенты a, b, c, d, e, f и правая часть g могут зависеть от переменных x, y и искомой функции u. В связи с этим уравнение может быть: 1) с постоянными коэффициентами; б) линейным, если g линейно зависит от u, а коэффициенты зависят только от x, y; в) квазилинейным, если коэффициенты зависят от u. Уравнение (1) – это самый общий вид.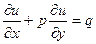 , (2)
, (2) оно может принадлежать к одному из трех типов: гиперболическому (D > 0), параболическому (D = 0) или эллиптическому (D < 0).
оно может принадлежать к одному из трех типов: гиперболическому (D > 0), параболическому (D = 0) или эллиптическому (D < 0). (3)
(3) , a>0 (4)
, a>0 (4) (5)
(5)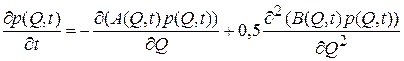
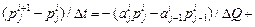
 ,
, . В качестве начального условия берется гистограмма (см. рис. 3.6 б) с условием нормировки
. В качестве начального условия берется гистограмма (см. рис. 3.6 б) с условием нормировки  . Расчет производится последовательно по временным шагам в соответствии с алгоритмом
. Расчет производится последовательно по временным шагам в соответствии с алгоритмом .
.
 От указанных недостатков свободна неявная схема, хотя сам алгоритм расчета по ней существенно усложняется. Рассмотрим метод прогонки. Конечно-разностная аппроксимация уравнения ФПК имеет вид:
От указанных недостатков свободна неявная схема, хотя сам алгоритм расчета по ней существенно усложняется. Рассмотрим метод прогонки. Конечно-разностная аппроксимация уравнения ФПК имеет вид: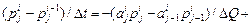
 ,
, , (3.27)
, (3.27) ,
,  ,
, .
. ,
, . (3.28)
. (3.28) ,
,  .
. . (3.29)
. (3.29) и
и  :
: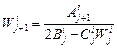 ,
,  . (3.30)
. (3.30) берутся из начального условия. Формулы (3.30) реализуют прогонку левого граничного условия в прямом направлении.
берутся из начального условия. Формулы (3.30) реализуют прогонку левого граничного условия в прямом направлении. находим по (3.28), начиная с правого граничного условия (обратная прогонка).
находим по (3.28), начиная с правого граничного условия (обратная прогонка). возникают проблемы физического характера, связанные с замыканием системы.
возникают проблемы физического характера, связанные с замыканием системы.