
|
|
Критерии оптимальности многофакторных12 Построение регрессионных моделей статических объектов В условиях неопределённости В.Э. Дрейзин The building multimeasured regression models of static objects In conditions of indefinite V. E. Dreizin The different strategies building of regression models complicated static objects in conditions of indefinite factors space is present. Necessity used the strategy inclusion step by step is showed. Analysis of possible criterions optimal of models is conducted and use of D-criterion on selection best model of every step and model optimal complication is based one’s arguments on facts. The possible of building non linear model on used that criterion is considered. The general procedure building of models complicated objects in conditions of indefinite factors space and form of model is described. Рассмотрены различные стратегии построения регрессионных моделей сложных статических объектов в условиях неопределённости факторного пространства. Показана необходимость использования пошаговой стратегии включения. Проведён анализ возможных критериев оптимальности моделей и обосновано использование D-критерия при выборе наилучшей модели каждого шага и модели оптимальной сложности. Рассмотрена возможность построения нелинейных моделей с использованием того же критерия и описана общая процедура построения моделей сложных объектов в условиях неопределённости исходного факторного пространства и вида модели. 1. Выбор стратегии построения регрессионной модели в условиях неопределённости факторного пространства
Для построения математических моделей сложных статических объектов при неизвестном механизме их функционирования широко применяется метод многофакторного регрессионного анализа, при котором математическая модель строится по опытным данным, т.е. измеренным в процессе нормального функционирования объекта значениям результативных и факторных признаков, характеризующих данный объект [1]. В большинстве реальных задач отсутствуют чёткие априорные сведения о перечне факторных признаков, от которых зависит выходная величина (результативный признак) исследуемого объекта. Особенно это относится к задачам построения математических моделей социально-экономических объектов. В этих условиях, исходя из требований информационной полноты, всегда стремятся включить в исходное факторное пространство все факторы, от которых может зависеть выходная величина. Т.е. из боязни упустить хотя бы один существенный фактор мы готовы идти на значительную избыточность исходного факторного пространства, с тем, чтобы факторы, оказавшиеся несущественными, отсеять потом, уже при построении математической модели объекта. При этом многие факторные признаки, включённые в исходное факторное пространство могут существенно коррелировать друг с другом, что дополнительно осложняет построение регрессионной модели. В отличие от классической регрессионной задачи для полностью определённого факторного пространства, независимых факторных признаках и линейного вида математической модели, в математической статистике не существует однозначного метода решения регрессионной задачи в условиях неопределённости мерности факторного пространства и вида математической модели [2]. При избыточной мерности факторного пространства на первый взгляд наиболее логичным представляется метод решения, базирующийся на стратегии исключения. Он подразумевает построение наиболее полной регрессионной модели по всем факторным признакам, учитываемым в исходном факторном пространстве, а затем уже анализ каждого члена модели на существенность и отбрасывание всех несущественных членов модели (для чего математическая статистика имеет достаточно надёжные критерии). Такой метод был бы безупречен, если бы все факторные признаки были бы независимыми или хотя бы слабокоррелированными. Но в реальных задачах это требование не выполняется, а при существенной взаимной корреляции хотя бы части факторных признаков матрица исходных данных ХТХ (или построенная по ней матрица дисперсий-ковариаций), по которой вычисляются коэффициенты уравнения регрессии, становится плохообусловленной, т.е. её определитель стремится к нулю. А при этом обращение матрицы (что необходимо для вычисления коэффициентов регрессии) становится невозможным. Более того, даже если матрицу удаётся обратить, то построенная модель становится неустойчивой. Это означает, что при небольших изменениях факторов могут происходить большие изменения выходной величины. Такая модель будет иметь очень плохую предсказательную способность, и пользоваться ей практически нельзя. Кроме того, при больших мерностях задачи даже при независимых факторах обращение матрицы высокого порядка становится затруднительным даже для современных ЭВМ, требуя огромного объёма вычислений. Все эти причины при большой начальной мерности задачи исключают возможность применения алгоритмов, базирующихся на методе исключения. Остается ещё два возможных пути. Первый из них состоит в том, чтобы ещё до построения регрессионной модели исключить из начального множества факторов все незначимые и сильно коррелирующие между собой факторы. Казалось бы математическая статистика располагает для этого такими весьма мощными методами как дисперсионный, корреляционный и факторный анализы. Однако при детальном рассмотрении оказывается, что все эти методы применительно к данной задаче имеют существенные ограничения. В самом деле, дисперсионный анализ вообще практически не применим в условиях пассивного эксперимента, поскольку для его успешного применения необходимо для каждого исследуемого фактора иметь такие группы наблюдений, в которых изменялся бы только данный фактор при постоянстве всех остальных. Совершенно очевидно, что при большом количестве факторов в условиях пассивного эксперимента даже из очень большого объёма наблюдений выделить такие группы для каждого из факторов совершенно нереально. Корреляционный анализ тоже имеет серьёзные ограничения. Действительно, парные коэффициенты корреляции при большом числе одновременно меняющихся факторов уже не могут дать надёжного представления о степени взаимосвязи любого из этих факторов с выходной величиной и друг с другом даже при линейных зависимостях. А если ещё моделируемые зависимости существенно нелинейны, то их вообще нельзя использовать в качестве количественных характеристик тесноты связи. От первого из этих ограничений можно было бы избавиться, применяя вместо парных частные коэффициенты корреляции. Однако, для вычисления частных коэффициентов корреляции в многомерных задачах должна быть построена и обращена полная матрица дисперсий-ковариаций для всех исходных факторов, включая и выходную величину. А, следовательно, здесь возникают те же самые трудности, которые не дают возможность использования методов, базирующихся на стратегии исключения. Что же касается второго ограничения, связанного с моделированием нелинейных зависимостей, для преодоления которого, в принципе, можно было бы вместо коэффициентов корреляции использовать корреляционные отношения, то, во-первых, они могут использоваться лишь вместо парных коэффициентов корреляции, а во-вторых, для многомерной задачи их вычисления очень громоздки. Таким образом, обойти ограничения, присущие корреляционному анализу, применительно к данной задаче не удаётся. Что же касается факторного анализа и, в частности, метода главных компонент, то он фактически уводит нас от исходной задачи – сокращения мерности исходного факторного пространства. Действительно, хотя метод главных компонент позволяет так сконструировать новое факторное пространство, что его мерность окажется существенно меньше мерности исходного факторного пространства, а все факторы в этом новом пространстве будут ортогональны (т.е. независимы друг от друга), но все эти новые факторы будут являться линейными комбинациями исходных факторных признаков, мерность пространства которых остаётся неизменной. Более того, все трудности, связанные с обращением исходной матрицы дисперсий-ковариаций (или заменяющей её корреляционной матрицы), а также с неустойчивостью решений, получаемых при плохо обусловленных матрицах, здесь сохраняются в полной мере, только переносятся из модели главных компонент в процедуру вычисления линейного оператора (представляющего собой матрицу коэффициентов размерностью n×n, где n – число факторных признаков в исходном факторном пространстве), преобразующего исходное факторное пространство в факторное пространство главных компонент. Таким образом, ни один из рассмотренных методов статистического анализа не позволяет эффективно решить задачу исключения незначимых и сильно коррелирующих между собой факторных признаков из первоначального избыточного факторного пространства. Поэтому единственной приемлемой стратегией построения оптимальной регрессионной модели при большой начальной мерности факторного пространства и взаимно коррелированных факторных признаках является стратегия включения. Данная стратегия подразумевает пошаговое наращивание мерности пространства учитываемых моделью факторных признаков с анализом на каждом шаге степени оптимальности построенной модели. Таким образом, отсеивание малозначимых и сильно коррелирующих с уже включёнными в модель факторных признаков должно происходить в процессе построения регрессионной модели. Алгоритм построения оптимальной регрессионной модели при использовании стратегии включения будет выглядеть следующим образом. На первом этапе строится оптимальная линейная регрессионная модель. Для этого применяется пошаговая процедура. На первом шаге строится однофакторная линейная модель. Отбор первого наиболее информативного факторного признака не представляет затруднений. Среди однофакторных линейных моделей наилучшей будет та, в которой используется фактор, имеющий максимальный парный коэффициент корреляции с выходной величиной. Но уже на следующем шаге использовать коэффициент корреляции с выходной величиной в качестве критерия для отбора следующего факторного признака (для построения двухфакторной оптимальной модели) не представляется возможным, т.к. вполне вероятным может оказаться случай, что максимальным коэффициентом корреляции с выходной величиной будет обладать фактор, тесно коррелирующий с уже отобранным на первом шаге фактором. В этом случае полученная двухфакторная модель будет немного точнее, чем однофакторная, но окажется уже неустойчивой относительно новых данных. В качестве критерия отбора следующего факторного признака на втором и последующих шагах вполне корректно было бы использовать частные коэффициенты корреляции при условном постоянстве уже отобранных на предыдущих шагах факторов (сначала одного, потом двух и т.д.). Но вычисление этих частных коэффициентов корреляции ничуть не проще, чем вычисление коэффициентов соответствующих регрессионных моделей при поочерёдном включении каждого из оставшихся факторов. Поэтому гораздо проще и надёжней будет на втором шаге поочерёдно включать каждый из оставшихся после первого шага факторов с построением соответствующих двухфакторных моделей и по тому или иному критерию оптимальности модели выбирать среди них оптимальную. После этого можно переходить к третьему шагу и к двум уже выбранным факторам по очереди добавлять каждый из оставшихся, строя трёхфакторные модели и выбирая из них наилучшую и т.д. Причём критерий оптимальности модели, используемый для выбора наилучшей модели на каждом шаге, должен быть пригоден и для сравнения наилучшей модели данного шага с наилучшей моделью предыдущего шага, с тем, чтобы определить: привело ли очередное наращивание мерности факторного пространства к существенному улучшению модели или нет. Тогда появляется возможность остановки алгоритма на том шаге, после которого прибавление следующих факторов уже не приводит к её существенному улучшению. Обсуждение подходящих для этого критериев оптимальности модели проведено ниже.
Критерии оптимальности многофакторных Регрессионных моделей
Математическая статистика в качестве критерия точности построенной регрессионной модели относительно тех выборочных данных, по которым она строилась, предлагает остаточную дисперсию
где Этот критерий показывает, насколько существенно построенная регрессионная модель снижает общую дисперсию выходной величины. При этом сама остаточная дисперсия является характеристикой точности построенной модели относительно тех данных, по которым она была построена. Казалось бы, она вполне пригодна для использования в качестве критерия для отбора наилучшей регрессионной модели. Но здесь возникает две проблемы. Первая из них связана с предсказательной точностью модели, а вторая с её способностью сглаживать “шум” выборки, вызванный неизбежными погрешностями, возникающими при измерении факторных и выходного признаков. Под предсказательной точностью модели понимают её точность относительно новых значений факторных признаков, не участвовавших в построении самой модели. Её можно характеризовать остаточной дисперсией данной модели относительно другой выборки данных, взятой из той же генеральной совокупности. Совершенно понятно, что предсказательная точность модели для всех практически важных случаев является более важной, чем точность модели относительно тех данных, по которым данная модель была построена. Конечно, предсказательная точность модели будет напрямую зависеть от представительности (репрезентативности) той выборки, по которой она была построена. Поэтому для выборок достаточно больших объёмов (N>>n), взятых из генеральной совокупности при одинаковых условиях (т.е. имеющих равную репрезентативность) остаточные дисперсии для обучающей выборки (по которой была построена модель) и для проверочной выборки будут практически одинаковы (конечно, пока число факторов, включённых в модель остаётся много меньше объёма каждой выборки, т.е. пока модель далека от насыщения и хорошо сглаживает “шум” выборки). Но при уменьшении объёмов выборок остаточные дисперсии по обучающей и проверочной выборкам ведут себя совершенно по разному по мере усложнения самих регрессионных моделей (т.е. по мере включения в неё большого числа факторов). Если остаточная дисперсия по обучающей выборке при включении в модель каждого последующего фактора монотонно убывает, то остаточная дисперсия по проверочной выборке убывает лишь на первых шагах усложнения модели, а, начиная с какого-то шага (что зависит от объёма выборок), начинает возрастать, образуя чёткий минимум. Если при этом обе выборки ещё можно считать репрезентативными, то этот минимум будет соответствовать той предельной сложности модели, при которой она ещё хорошо сглаживает “шум” выборки. Если же объём выборок настолько мал, что считать их репрезентативными нельзя, то такой минимум наступит гораздо раньше в силу расхождения самих выборок, т.к. ни та, ни другая не будут адекватно представлять генеральную совокупность. Но хотя оптимальная сложность модели в этом случае ещё не будет достигнута, всё равно дальнейшее усложнение модели становится не только бессмысленным, но и вредным, т.к. предсказательная точность модели будет при этом падать. Таким образом, минимум остаточной дисперсии по проверочной выборке является надёжным критерием для прекращения дальнейшего наращивания мерности модели при любом объёме выборок. А поскольку эта дисперсия характеризует предсказательную точность модели, которая более важна, чем точность модели для обучающей выборки, то, в принципе, остаточную дисперсию по проверочной выборке можно использовать в качестве критерия оптимальности модели и при отборе наилучшей модели каждого шага, и при выборе модели оптимальной сложности. Но для окончательного выбора критерия необходимо рассмотреть ещё одну проблему – проблему устойчивости регрессионных моделей. Как уже упоминалось выше, основной причиной неустойчивости регрессионных моделей является включение в модель неортогональных друг к другу факторов, т.е. взаимная корреляция этих факторов. Следует заметить, что использование в качестве критерия отбора очередного фактора в модель остаточной дисперсии само по себе автоматически приводит к отбору на каждом новом шаге именно того фактора, который, достаточно сильно коррелируя с выходной величиной (результативным признаком), слабо коррелирует с уже включёнными в модель факторными признаками. Это понятно, поскольку, если отбираемый очередной факторный признак будет тесно коррелировать с одним из уже включённых факторов, то данный признак будет нести мало дополнительной информации, а, следовательно, не будет приводить к существенному уменьшению остаточной дисперсии. Однако, такое положение сохраняется лишь на первых шагах стратегии включения, когда ещё остаётся достаточно большой выбор для включения очередного фактора, (т.е. пока соблюдается условие n>>l, где n – начальная мерность факторного пространства, l – число уже отобранных в модель на предыдущих шагах факторных признаков). А когда среди оставшихся факторных признаков будут оставаться только либо несущественные, либо достаточно сильно коррелирующие с факторными признаками, уже включёнными в модель на предыдущих шагах, то среди последних будет отобран фактор, наиболее слабо (по сравнению с оставшимися) коррелирующий с уже включёнными ранее факторными признаками, но тем не менее, эта корреляционная связь окажется уже существенной. Наличие в модели достаточно тесно коррелирующих между собой факторных признаков может приводить к двум нежелательным последствиям. Во-первых, ковариационная матрица становится близкой к вырожденной, т.е. её определитель становится очень близким к нулю, а значит, обращение такой матрицы становится затруднительным. Во-вторых, даже если ЭВМ справится с обращением такой матрицы, то найденное уравнение регрессии становится неустойчивым, т.е. при небольших вариациях исходных данных (которые могут вызываться погрешностями их измерений) вычисленные по этому уравнению значения выходной величины могут изменяться весьма значительно. А это означает, что предсказательная точность такой модели будет очень низкой. Чтобы этого избежать, необходимо при отборе очередного факторного признака исключить возможность получения неустойчивой модели. Такая возможность может появляться лишь в тех случаях, когда и обучающая, и проверочная выборки достаточно представительны и их объём весьма велик. В этом случае, при пошаговом усложнении модели согласно изложенному выше алгоритму, остаточные дисперсии и по обучающей, и по проверочной выборкам будут монотонно убывать и незначительно отличаться друг от друга. Поэтому критерий в виде
где: sм – погрешность математической модели;
k – текущая мерность модели; не будет давать чёткого минимума, даже когда в модель начнут включаться признаки, тесно коррелирующие с уже включёнными ранее. При этом коэффициенты при положительных и отрицательных членах регрессионной модели будут увеличиваться по абсолютной величине, что и будет приводить к неустойчивости решения (результирующая величина Y, вычисляемая как разность между положительными и отрицательными членами модели, окажется по абсолютной величине много меньше самих этих членов). Чтобы этого избежать, необходимо дополнить критерий (1) членом, который бы минимизировал сумму квадратов всех коэффициентов регрессионной модели. Это можно сделать, если интерпретировать определение выходной величины Y, по измеренным значениям факторных признаков, включенных в модель, как косвенное измерение величины Y. Тогда можно воспользоваться известной формулой для погрешности косвенных измерений:
где: sYинс – инструментальная погрешность выходной величины Y, определяемая инструментальными погрешностями измерений факторных признаков sXj ; bj – коэффициенты регрессионной модели, соответствующие учитываемым факторам Xj; l – число факторов, включённых в модель. Совершенно очевидно, что с ростом сложности модели sY.инс будет монотонно возрастать. Но пока модель остаётся устойчивой, каждый вновь добавляемый член модели будет вносить всё меньший вклад в результирующую величину, а коэффициенты при ранее включенных факторах будут изменяться незначительно (в предельном случае, если все факторы независимы, то они вообще не меняются). Но как только в модель начнут включаться факторы, тесно коррелирующие с уже включёнными ранее, положение резко меняется. Все коэффициенты начинают существенно возрастать, а следовательно, и sYинс резко увеличивается. Общую погрешность выходной величины Y, рассчитываемой по построенной модели, можно определить как
Совершенно очевидно, что наилучшей предсказательной способностью будет обладать модель, отвечающая условию min sY при последовательном наращивании её мерности. Поэтому его можно использовать и при подборе наилучшего факторного признака из оставшихся при каждом очередном шаге усложнения модели, и при сравнении наилучшей модели очередного шага с наилучшей моделью предыдущего шага. Выражение (3) справедливо лишь для линейных моделей. Но нетрудно получить аналогичные выражения и для нелинейных моделей. В частности, для широко применяемых полиномиальных моделей второго порядка соответствующее выражение будет иметь вид
где bjj – коэффициенты при квадратичных членах модели; bjq – коэффициенты при попарных произведениях факторов;
Комплексный критерий (3) был впервые введён в [3] применительно к многопараметровому неразрушающему контролю и назван D-критерием. В дальнейших работах [4-6] было исследовано его поведение методом имитационного математического моделирования в зависимости от объёма обучающей и проверочной выборок, степени стохастичности искомых зависимостей, величины инструментальных погрешностей, степени взаимной коррелированности факторных признаков и при различных законах распределения выборочных данных, а также на реальных задачах не только по многопараметровому неразрушающему контролю, но и задачах построения математических моделей различных технологических процессов и социально-экономических объектов и систем. Это исследование убедительно показало, что D-критерий эффективен и как критерий выбора очередного факторного признака для включения в модель, и как критерий прекращения дальнейшего наращивания сложности модели при пошаговой стратегии включения для всех моделируемых условий. При малых объёмах выборок D-критерий начинает расти уже после первых трёх-четырёх шагов. Это определяется начинающимся ростом остаточной дисперсии по проверочной выборке (
где В условиях же представительности обеих выборок с увеличением сложности модели остаточные дисперсии и по обучающей, и по проверочной выборкам будут вести себя примерно одинаково (т.е. монотонно убывать с ростом числа членов модели) до тех пор, пока модель далека от насыщения (т.е. l<<Nоб). Однако, как уже было сказано выше, модель может начать терять устойчивость. Именно от этого предохраняет введение в D-критерий инструментальной погрешности. Действительно, при росте числа членов модели рост величины σYинс резко ускоряется. В это же время σм продолжает монотонно уменьшаться, но скорость уменьшения с каждым новым шагом замедляется. В итоге, когда скорость роста σYинс превысит скорость уменьшения σм, D-критерий начнёт возрастать. В этом случае алгоритм будет остановлен при достижении глобального минимума D-критерия. Причём, это произойдёт задолго до достижения насыщения модели даже при малой степени стохастичности моделируемых зависимостей и высокой точности измерения факторных признаков. Имитационное моделирование показало, что эффективность D-критерия не снижается и в условиях взаимной корреляции факторных признаков, и при существенных отклонениях закона распределения выборочных данных от нормального. В частности, было исследовано его поведение не только для нормального закона распределения выборочных данных, но и для равномерного и двухмодального нормального закона. Поэтому его можно рекомендовать для построения оптимальных регрессионных моделей статических объектов и систем в условиях неопределённости факторного пространства.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 или среднеквадратическую навязку
или среднеквадратическую навязку  . Сам метод наименьших квадратов, лежащий в основе вычислений коэффициентов регрессионной модели, при заданной выборке исходных данных и заданной совокупности факторов минимизирует именно эти величины. Регрессионная модель считается адекватной, если остаточная дисперсия существенно меньше общей исходной дисперсии выходной величины:
. Сам метод наименьших квадратов, лежащий в основе вычислений коэффициентов регрессионной модели, при заданной выборке исходных данных и заданной совокупности факторов минимизирует именно эти величины. Регрессионная модель считается адекватной, если остаточная дисперсия существенно меньше общей исходной дисперсии выходной величины: ,
, табличное значение критерия Фишера для выбранного значения доверительной вероятности P и числа степеней свободы числителя
табличное значение критерия Фишера для выбранного значения доверительной вероятности P и числа степеней свободы числителя  и знаменателя
и знаменателя  , где N – объём выборки, по которой строилось уравнение регрессии, l – число факторов построенной регрессионной модели.
, где N – объём выборки, по которой строилось уравнение регрессии, l – число факторов построенной регрессионной модели. , (1)
, (1) – остаточные дисперсии соответственно по обучающей и проверочной выборкам;
– остаточные дисперсии соответственно по обучающей и проверочной выборкам; , (2)
, (2)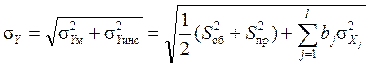 . (3)
. (3) ,
, cредние значения факторов Хj и Хq .
cредние значения факторов Хj и Хq . ) из-за статистической неидентичности обучающей и проверочной выборок при их недостаточном объёме. Это означает, что при дальнейшем усложнении модель становится неадекватной генеральной совокупности. Проверить это легко по критерию Фишера
) из-за статистической неидентичности обучающей и проверочной выборок при их недостаточном объёме. Это означает, что при дальнейшем усложнении модель становится неадекватной генеральной совокупности. Проверить это легко по критерию Фишера (4)
(4) - табличное значение критерия Фишера для доверительной вероятности P и степеней свободы υ1= (Nпр – 1) и υ2 = (Nоб – 1), где Nпр и Nоб – объёмы проверочной и обучающей выборок. Поэтому после каждого очередного шага следует производить проверку по (4) и, если неравенство выполняется, то останавливать алгоритм независимо от того, достигнут ли глобальный минимум D-критерия или нет.
- табличное значение критерия Фишера для доверительной вероятности P и степеней свободы υ1= (Nпр – 1) и υ2 = (Nоб – 1), где Nпр и Nоб – объёмы проверочной и обучающей выборок. Поэтому после каждого очередного шага следует производить проверку по (4) и, если неравенство выполняется, то останавливать алгоритм независимо от того, достигнут ли глобальный минимум D-критерия или нет.