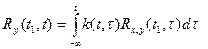|
|
Система случайных функцийДифференцирование и интегрирование случайных функций.
Основные понятия: Для того чтобы могли существовать предельные переходы, входящие в понятия дифференциала и интеграла должно выполнятся условие:
x(t) – предел последовательности функций x1(t), x2(t)…. xn(t) если:
а) б)
x(t) дифференцируема в точке t0 если:
Предел рассматривается в смысле среднего квадрата:
Необходимое условие дифференцируемости
Должно выполняться следующее условие непрерывности / т.к. числитель и знаменатель должны быть одного порядка малости/.
отсюда:
Когда
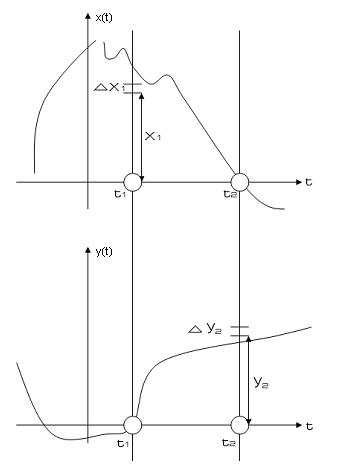
Достаточное условие дифференцируемости: Для разных схем приращений Δ1 и Δ2 должен быть один и тотже предел: Пределы должны быть одинаковы в смысле среднего квадрата:
Выражение под знаком предела :
отсюда предел:
Данное выражение = 0, если существует вторая производная от корреляционных функций при равных значениях аргумента.
Частный случай. Стационарные процессы.
R(t1,t2)=R(t2-t1)
Условие достаточности:
Должна существовать 2-ая производна при
Вычисление характеристик случайной функции x/(t)=v(t) по характеристикам случайного процесса x(t) Известна: Rx(t1,t2) – характеристика процесса x(t) Найти: Rv=?
Считаем По определению:
Интегрируемость
  x(t) y(t) x(t) y(t)
Вычисление характеристик случайных функций y(t), являющихся интегралом от x(t), по характеристикам x(t) Для операции дифференцирования нужно было понятие непрерывность, при интегрировании это не обязательно, тут нет требования соразмерности величин. Здесь будет много слагаемых, следовательно, нужно, чтобы суммы были не бесконечными - это и есть необходимое условие.
Интеграл есть предел частных сумм:
Предел рассматривается в смысле среднего квадрата (l.i.m.)
Самое большое слагаемое должно быть конечным.
Отсюда: интегрирование возможно если, существует(конечный) двойной интеграл от корреляционной функции интегрируемого процесса. Как найти корреляционную функцию процесса на выходе интегратора по корреляционной функции процесса интегрируемого: По определению:
Операция вычисления математического ожидания – это осреднение случайных процессов в фиксированный момент времени (не путать с конкретным алгоритмом нахождения корреляционных функций, где используется гипотеза эргодичности, там вычисления по ансамблю заменяются вычислениями по реализации). Действие на случайный процесс линейных операторов, таких как интегрирование, дифференцирование и т.д. – это действие на процесс в различные моменты времени. Действия линейных операторов и операторов осреднения независимы. Их порядок можно менять местами.
Действие линейного оператора общего вида на случайный процесс
Линейный оператор(пример): y(t)= Ранее были уже рассмотрены частные случаи – интегрирование и дифференцирование
время, в которое действует оператор
Известны Определить а) Система случайных функций
Мы ранее рассматривали каждый процесс сам по себе и у него были собственные свойства, такие характеристики называются автокорреляционными, чтобы не путать с другой характеристикой, взаимокорреляционной функцией, когда рассматривается несколько функций.
Для системы функций: x(t), y(t) вводятся многомерные законы распределения: P(x1,y2,t1,t2) Больше чем двумерными законами в инженерной практике приборных предприятий пока обычно не пользуются. Пользуются, как правило, моментными характеристиками. Взаимнокорреляционная функция:
Если процессы стационарные и эргодические то вычисление оценки
Свойство взаимнокорреляционной функции:
Взаимнокорреляционная функция между x и его производной v(x)
Частный случай для стационарных процессов:
Замечание: если процесс х дифференцируемый, то при
1.8.2.4 Корреляционная взаимосвязь между входным и выходным процессами и импульсно-переходной функцией k(
Решение (выходной сигнал) для устойчивой системы с закончившимися переходными процессами: (нулевое свободное движение) y(t)=
  x(t) y(t) x(t) y(t)
Взаимосвязь входного и выходного сигнала для времени t:
запишем это выражение, помножив левую и правую часть на x(t1):
Вычислим математическое ожидание:
Внутренний интеграл, не что иное как: Отсюда:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
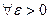

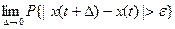 =0
=0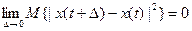
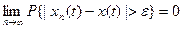 - предел по вероятности.
- предел по вероятности. - предел в смысле среднего квадрата
- предел в смысле среднего квадрата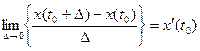 - производная от предела x(t) в точке t0.
- производная от предела x(t) в точке t0.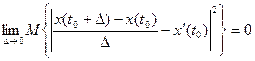

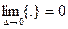 ? – Если корреляционная функция процесса x будет непрерывной функцией своих аргументов
? – Если корреляционная функция процесса x будет непрерывной функцией своих аргументов 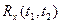
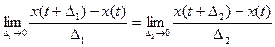
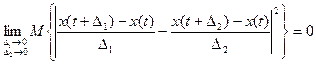
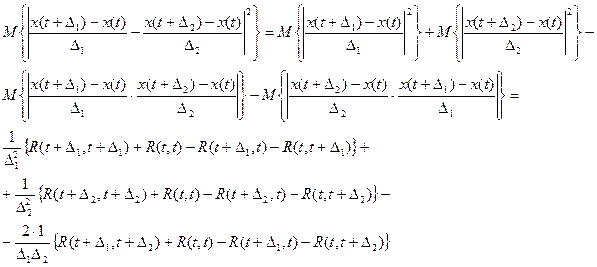
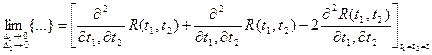
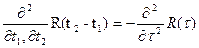 (
( 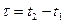 )
)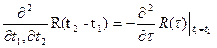
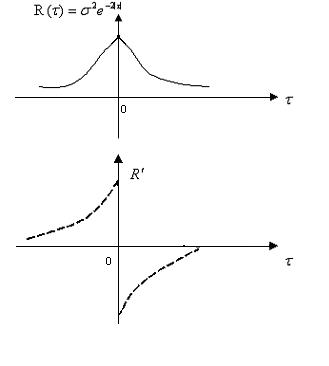
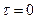
 - существует при
- существует при 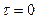


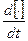
 ;
; 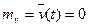

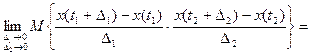
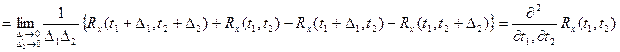 Частный случай для стационарных процессов:
Частный случай для стационарных процессов: 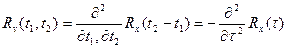
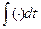
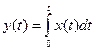
 - интеграл
- интеграл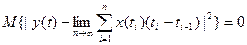
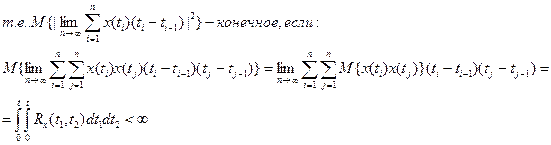
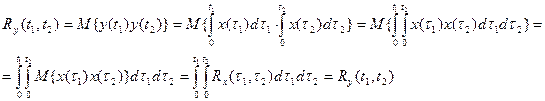
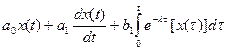
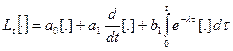
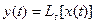

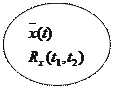




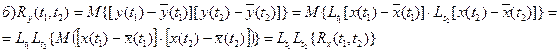
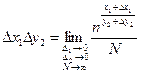
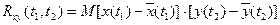 (это осреднение по ансамблю)
(это осреднение по ансамблю)
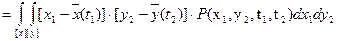
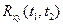 существенно упрощается:
существенно упрощается: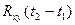 =
= 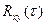 =
= 
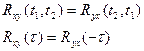
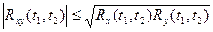
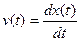
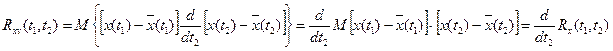
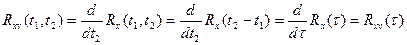
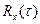 равна нулю т.е.
равна нулю т.е. 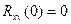
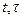 ).
).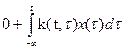
 ;
; ;
;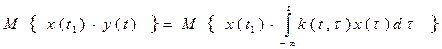 ;
;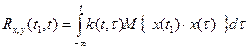 ;
;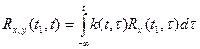 ( выражение очень важное в методах ретроспективной идентификации)
( выражение очень важное в методах ретроспективной идентификации)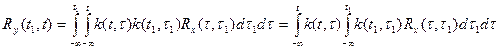 ;
;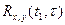 ;
;