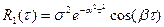|
|
Случайные процессы в системах автоматического управления.12 Как уже отмечалось процессы бывают детерминированными то есть наблюдение дает возможность предсказать дальнейшее поведение. Индетерминированные процессы. Сколько не наблюдаем, не знаем как прогнозировать. Случайные процессы (промежуточные процессы). Точно предсказать не можем. Есть механизм, который не знаем (скрытый параметр), но можем найти некоторые характеристики, которые позволяют описывать общие свойства в поведении процесса. Эти характеристики знает только Господь Бог. У случайных процессов характеристики являются неслучайными. Но мы их находим из экспериментов, поэтому они точно быть выявлены не могут. Говорят, что для описания процессов используются оценки (случайные числа) Теория оценивания занимается нахождением этих характеристик. Там есть требования : - несмещенность - состоятельность - эффективность Наиболее общим описанием случайных параметров является многомерные законы распределения случайных процессов. Случайные процессы в любой момент времени является случайной величиной. Значение процессов в различные моменты времени связанны. Степень взаимосвязи может быть разной. Если задан n-мерный закон распределения, то считается, что случайный процесс полностью задан. К сожалению, пользоваться законами распределения очень затруднительно из-за громоздкости и слабой обозримости. Поэтому в технике, пытаясь сократить громоздкость, не пытаются максимально точно изучать случайные процессы, а используют их для получения оценок в конкретных технических задачах. Одной из самых главных задач для систем управления - это оценить величину ошибки, которая появляется из-за того, что тот процесс является случайным. Как выбрать параметр системы, чтобы ошибка была минимальной? Такие две задачи удается решать и без полного описания. Поэтому есть раздел «Корреляционная теория случайных процессов»
Общие понятия
Наиболее общим и полным описанием является n-мерный закон : P( Являющийся функцией 2-х переменных:
t1 t2 t3 t4 tN
N значений x
Удобнее пользоваться не законами вероятность, а плотностью вероятности. **
Стационарные процессы - это процессы, у которых при описании случайных процессов, то есть при задании законов распределения, существует свойство: абсолютное значение времени на вид закона не влияет. Играет роль только относительное расположение точек t1, t2, …tn.
Наличие стационарности упрощает вид многих форму. Достаточно знать только расстояние между точками (сдвиг). Эргодичность процесса.
При первой возможности пытаются трактовать так: эргодичность означает, что вычисление характеристики по ансамблю можно заменить вычислением характеристики по реализации. Существует тест на эргодичность. Многие процессы не являются стационарными. Их пытаются все описывать как стационарные, а учитывают нестационарность специальными дополнительными вычислениями. Одномерная плотность распределения вероятности.
Двумерный закон распределения
Итого получается, смотри **
Процессы, у которых идет учет значений только для одного предыдущего момента вращения, называются марковскими. Для решения ряда технических задач можно обойтись моментными характеристиками. Самыми важными моментными характеристиками являются первые и вторые, начальные и центральные моменты. Теория, которая оперирует только с первыми и вторыми начальными и центральными моментами, называется корреляционной теорией.
1. Начальный момент – математическое ожидание
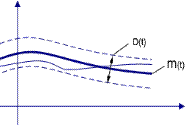
2. Второй момент – дисперсия D(t)= 3. Корреляционная функция
Математическое ожидание оценивает среднее значение процесса. Дисперсия оценивает разброс относительно математического ожидания. Корреляционная функция характеризует степень линейной взаимосвязанности между случайной производной по времени. Если корреляционная функция такова, что она уменьшается у одного процесса для одних и тех же сдвигов момента времени, больше, чем у другого процесса, то это значит, что данный процесс имеет меньшую степень взаимосвязанности. Если выполняется гипотеза эргодичности и процессы стационарные, то получается, что процесс не зависит от абсолютного значения момента времени, одномерная плотность распределения будет одинакова для любого t1 момента времени : p(x1). Двумерная плотность зависит лишь от разности моментов времени (сдвига : 1. Математическое ожидание По гипотезе стационарности : m По гипотезе эргодичности : 2. Не зависит от времени дисперсия (стационарность и эргодичность) :
4. Если процесс стационарный, играет роль только разница между t1 и t2
k – дискретный сдвиг
Если сдвига нет, то получается дисперсия. Примеры: Гауссовы законы плотности распределения случайного процесса
здесь: k1(t2-t1) , k2(t2-t1) , k3(t2-t1) некоторые функции.
Корреляционная теория для гауссовских законов является исчерпывающей. Зная корреляционные функции, можно записать закон распределения. k, k1, k2 соответствуют корреляционным функциям.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 )
)

 x2 x3
x2 x3
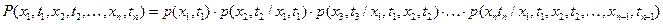
 N моментов времени
N моментов времени 2N
2N =
=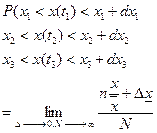
 - операция стационарности в узком смысле слова.
- операция стационарности в узком смысле слова.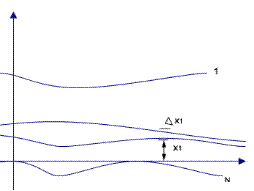
 - вероятность того, сколько траекторий прошло через диапазон
- вероятность того, сколько траекторий прошло через диапазон  , к общему числу траекторий.
, к общему числу траекторий.
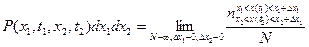
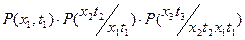

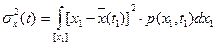
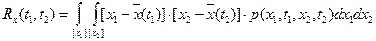
 ) : p(x1,x2,t).
) : p(x1,x2,t).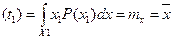

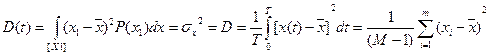
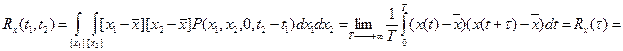
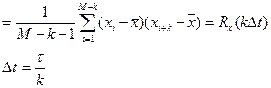
 t- шаг выборки процесса.
t- шаг выборки процесса.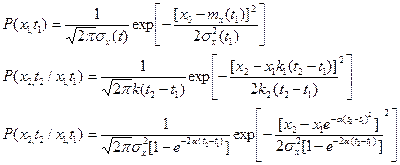
 В последней плотности распределения указан конкретный вид функций k1 , k2 , k3.
В последней плотности распределения указан конкретный вид функций k1 , k2 , k3.
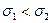
 В следующем примере (3-я строка) уточнение, один из конкретных видов. Если закон не Гаусса, то данная теория является первым приближением и решение является точным до вторых моментов.
В следующем примере (3-я строка) уточнение, один из конкретных видов. Если закон не Гаусса, то данная теория является первым приближением и решение является точным до вторых моментов.

 ;
; 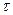

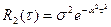 ;
;