
|
|
Расчетно-графическая работапо основам теории колебаний для студентов ФМФ
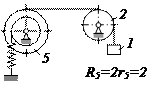
Механическая система с одной степенью свободы совершает малые колебания вблизи устойчивого положения равновесия. Учитывая силу сопротивления Схемы систем показаны на рис. 1, а необходимые данные приведены в табл. 1 и 2. В задании приняты следующие обозначения: 1 – груз массой m1; 2 – блок массой m2 и радиусом r2 (однородный сплошной диск); 3 – блок массой m3 и радиусом инерции Системы тел показаны в положении покоя при статической деформации пружин (рис. 1). В вариантах 5, 6, 14 и 23 стержень 6 жестко соединен с диском 4. Пример выполнения задания.Дано: m1 = 1 кг, m2 = 2 кг, m4 = 1 кг, m6 = 3 кг, 1 = 0,6 м, с = 2000 Н/м, b = 200 Н·с/м, Н = 50 Н. Определить амплитуду B вынужденных колебаний механической системы, а также найти ее максимальное значение
Рис. 1
Рис. 1
Рис. 1 Таблица 1
Таблица 2
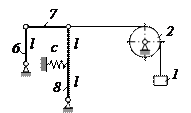
Решение. Выберем в качестве обобщенной координаты перемещение центра масс груза 1 из положения статического равновесия. Тогда уравнение Лагранжа 2 рода для механической системы, изображенной на рис. 2, можно записать в виде
Кинетическую T и потенциальную П энергию системы вычислим с точностью до величин второго порядка малости относительно величин y и Кинетическая энергия 1 тела
Блок 2 – однородный сплошной диск радиуса
Так как стержень 6 жестко соединен с блоком 2,
Учитывая, что
Тело 4 – однородный сплошной диск, совершающий плоскопараллельное движение. Его кинетическая энергия равна
где
Таким образом, кинетическая энергия рассматриваемой механической системы равна
Из последнего равенства определяем коэффициент инерции механической системы
Обобщенная сила, соответствующая потенциальным силам, может быть вычислена по формуле
где
а потенциальная энергия силы тяжести стержня –
где
Таким образом,
Потенциальная энергия пружины
где Потенциальная энергия всей системы
Статическую деформацию пружины определим из условия
Отсюда
Тогда
С другой стороны
При Обобщенная сила, соответствующая возмущающим силам
Обобщенная сила, соответствующая силам сопротивления
Подставляя выражения кинетической энергии и обобщенных сил в уравнение Лагранжа 2 рода, получим дифференциальное уравнение
Частное решение полученного уравнения, которое описывает вынужденные колебания, имеет вид
где
Так как параметры k и n найдены, величины B и ε являются функциями p – частоты возмущающей силы. Максимальное значение амплитуды B достигается при значениях p, удовлетворяющих условиям
где
Определим критические точки функции
Отсюда
Таким образом, функция
При резонансе
Анализируя полученные результаты, можно сделать вывод, что при малом сопротивлении

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и возмущающую силу
и возмущающую силу  , действующие на тело 1, пренебрегая другими силами сопротивления и массами нитей, определить амплитуду B вынужденных колебаний механической системы как функцию частоты возмущающей силы, а также найти ее максимальное значение
, действующие на тело 1, пренебрегая другими силами сопротивления и массами нитей, определить амплитуду B вынужденных колебаний механической системы как функцию частоты возмущающей силы, а также найти ее максимальное значение  и значение этой амплитуды при резонансе
и значение этой амплитуды при резонансе  . За обобщенную координату принять y – смещение тела 1 от положения статического равновесия.
. За обобщенную координату принять y – смещение тела 1 от положения статического равновесия. ; 4 – однородный сплошной диск массой m4 и радиусом r4; 5 – диск массой m5 и радиусом инерции
; 4 – однородный сплошной диск массой m4 и радиусом r4; 5 – диск массой m5 и радиусом инерции  ; 6 – тонкий однородный стержень массой m6 и длиной l; 7 – стержень, масса которого не учитывается; с – коэффициент жесткости пружины.
; 6 – тонкий однородный стержень массой m6 и длиной l; 7 – стержень, масса которого не учитывается; с – коэффициент жесткости пружины. 1
1
 2
2
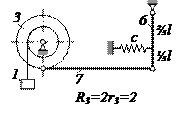 3
3
 4
4
 5
5


 6
6
 7
7
 8
8
 9
9
 10
10
 11
11
 12
12
 13
13
 14
14
 15
15
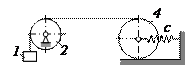 16
16
 17
17
 18
18

 19
19
 20
20
 21
21
 22
22
 23
23
 24
24
 25
25
 26
26
 27
27
 28
28

 29
29
 30
30
 м
м

 .
. .
.
 .
. , поэтому его кинетическая энергия определяется равенством
, поэтому его кинетическая энергия определяется равенством .
. ,
, .
. , получим
, получим .
. ,
, . Подставляя эти выражения в
. Подставляя эти выражения в  , получим
, получим .
. .
. кг.
кг. ,
, – потенциальная энергия сил тяжести, а
– потенциальная энергия сил тяжести, а  – потенциальная энергия пружины. Если принять в равновесном положении системы
– потенциальная энергия пружины. Если принять в равновесном положении системы  ,
, ,
, – угол поворота стержня. При малых y угол
– угол поворота стержня. При малых y угол  .
. .
. ,
, – статическая деформация пружины в равновесном положении системы (т.е. при y = 0);
– статическая деформация пружины в равновесном положении системы (т.е. при y = 0);  – дополнительная деформация пружины при перемещении тела 1 на y. Анализируя рис. 19, нетрудно доказать, что
– дополнительная деформация пружины при перемещении тела 1 на y. Анализируя рис. 19, нетрудно доказать, что  .
. .
. . Подставляя это значение в выражение для П, окончательно получим
. Подставляя это значение в выражение для П, окончательно получим .
. .
. . Приравнивая между собой правые части двух последних равенств, определяем коэффициент жесткости механической системы:
. Приравнивая между собой правые части двух последних равенств, определяем коэффициент жесткости механической системы: .
. положение равновесия механической системы устойчиво (в этом положении потенциальная энергия системы имеет минимум). Если
положение равновесия механической системы устойчиво (в этом положении потенциальная энергия системы имеет минимум). Если  , то положение равновесия неустойчиво.
, то положение равновесия неустойчиво. .
. .
. , где
, где – собственная частота колебаний;
– собственная частота колебаний;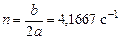 – коэффициент затухания;
– коэффициент затухания;  – относительная амплитуда возмущающей силы.
– относительная амплитуда возмущающей силы. ,
, – амплитуда;
– амплитуда;  – сдвиг по фазе вынужденных колебаний по отношению к фазе возмущающей силы.
– сдвиг по фазе вынужденных колебаний по отношению к фазе возмущающей силы. ,
, .
. :
: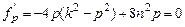 .
. (значение
(значение 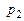 имеет физический смысл при
имеет физический смысл при  ). Знаки второй производной:
). Знаки второй производной: .
. и минимальное значение при
и минимальное значение при 
 . Тогда
. Тогда м.
м. , поэтому
, поэтому м.
м. .
.