
|
|
Расчет тепловой скорости движения электронов
Свободные электроны в металле образуют электронный газ. Рассчитаем скорость беспорядочного движения электронов в газе V , предполагая, что они подчиняются обычным газовым законам. Тогда кинетическая энергия движения электронов равна
где me – масса электрона, Эта энергия равна энергии теплового движения, которая определяется абсолютной температурой газа T
где k– постоянная Больцмана. Приравнивая (17) и (18) находим
Подставив значения для комнатной температуры t = 20 oC и справочные данные k = 1,38*10-23 Дж/К , me= 9*10-31 кг получим
Полученную скорость называют тепловой скоростью электронов Vтепл.
Задачи для самостоятельного решения 14. Рассчитать скорость теплового движения электронов в проводнике электронагревательной спирали из нихрома при температуре 600 оС по модели электронного газа. Справочные данные Постоянная Больцмана 1,38*10–23 Дж/К. Масса электрона 9,1*10–31 кг. Молярная масса никеля 59 г/моль.
15. Рассчитать скорость теплового движения электронов в медном проводнике, охлажденом до температуры жидкого азота –195 оС. Справочные данные Постоянная Больцмана 1,38*10–23 Дж/К. Масса электрона 9,1*10–31 кг. Молярная масса меди 64 г/моль.
Расчет электрической проводимости металлов Запишем закон Ома
Подставим в него выражение для сопротивления проводника
где l – длина проводника, S – его сечение , r – удельное сопротивление материала. Тогда
или
Учтя , что I / S = j есть плотность тока, U / l = E напряженность электрического поля, 1/ r = s удельная проводимость, получим закон Ома в локальной формулировке
Удельная проводимость s является свойством материала, которое, в свою очередь, зависит от характеристик движения электронов в металле. Найдем эти соотношения. Так как
из (25) и (26) получим
Обозначим
Величина m называется подвижностью носителей заряда. Тогда
Для расчета дрейфовой скорости электронов vдр воспользуемся моделью свободного движения электронов в промежутках между столкновениями с ионами кристаллической решетки. Среднее время свободного движения называется временем релаксации tрел , расстояние l преодолеваемое электроном за это время – длиной свободного пробега. Они связаны соотношением
За время движения между столкновениями, за счет действия силы со стороны электрического поля, электрон приобретает импульс p
с другой стороны этот импульс пропорционален приобретенной дрейфовой скорости
Приравнивая его к (31) находим
Подставим полученное выражение в (27) , получим
или, учтя (30),
В данную формулу входит неизвестная величина длины свободного пробега l . В качестве приблизительной оценки выберем ее равной десяти периодам кристаллической решетки металла.
Тогда подставив другие известные величины, получим, например, для меди величину удельной электрической проводимости
или для удельного электрического сопротивления
Сравнивая полученную величину с табличным значением
Задачи для самостоятельного решения 16. Как изменяется длина свободного пробега электронов в металлическом проводнике при его нагревании? 17. Во сколько раз изменится длина свободного пробега электронов при нагревании серебряного проводника от 300 до 1000 К? Удельное электрическое сопротивление серебра при комнатной температуре равно 0,015 Ом*м, температурный коэффициент сопротивления составляет 4,1*10–3 К–1. 18. Почему удельное электрическое сопротивление ферромагнитных металлов существенно выше неферромагнитных? 19. Рассчитать электропроводность медного проводника, приняв длину свободного пробега электронов в металле равной 5 нм. Справочные данные для меди Плотность 8,94 г/cм3 . Молярная масса 64 г/моль Число Авогадро 6,02*1023 моль–1. Заряд электрона 1,6*10–19 Кл.
20. Рассчитать электропроводность проводника из никеля, приняв длину свободного пробега электронов в металле равной 2 нм. Справочные данные для никеля: Плотность 8,9 г/cм3 . Молярная масса 59 г/моль Число Авогадро 6,02*1023 моль–1. Заряд электрона 1,6*10–19 Кл.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (18)
(18)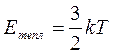 (19)
(19) (20)
(20)
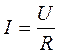 (21)
(21) (22)
(22) (23)
(23) (24)
(24) (25)
(25) (26)
(26) (27)
(27)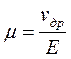 (28)
(28)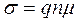 (29)
(29) (30)
(30) (31)
(31)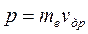 (32)
(32)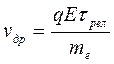 (33)
(33) (34)
(34) (35)
(35)


 , видим хорошее согласие с экспериментальными данными.
, видим хорошее согласие с экспериментальными данными.