|
|
Знакомство с методами измерения физических величин и оценкой погрешностей измеренийМИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОУ ВПО РЫБИНСКАЯ ГОСУДАРСТВЕННАЯ АВИАЦИОННАЯ ТЕХНОЛОГИЧЕСКАЯ АКАДЕМИЯ ИМЕНИ П.А. СОЛОВЬЕВА КАФЕДРА ОБЩЕЙ И ТЕХНИЧЕСКОЙ ФИЗИКИ
Лаборатория «Физические основы механики»
ЛАБОРАТОРНАЯ РАБОТА № ФМ-0 Знакомство с методами измерения физических величин и оценкой погрешностей измерений
Рыбинск 1995
ТРЕБОВАНИЯ ТЕХНИКИ БЕЗОПАСНОСТИ: Необходимо выполнение общих требований безопасности, установленных в лаборатории.
ЦЕЛЬ РАБОТЫ: Ознакомиться с прямыми и косвенными измерениями, методами обработки результатов измерений. Провести измерения линейных размеров тел, объемов, масс, плотностей.
ПРИБОРЫ И ОБОРУДОВАНИЕ: Штангенциркуль, микрометр, измеряемое тело, лабораторные весы.
1. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Введение Измерения – физические действия, заключающиеся в сравнении измеряемых величин с эталоном, принятым за единицу. Измерения разделяются на прямые (непосредственные) и косвенные. Прямые измерения проводятся приборами и инструментами. При косвенных измерениях искомая величина находится на основе функциональной зависимости между непосредственно измеренными величинами. Всегда следует помнить, что при любых измерениях нет возможности найти истинное значение измеряемых величин. Чтобы найти значение как можно более близкое к истинному, нужно проводить большее число измерений и на их основе вычислить среднее арифметическое значение. Чем больше число измерений, тем ближе среднее значение к истинному. Единицы измерения различных физических величин образуют систему единиц, построенную на основе ряда основных единиц и производных, полученных из функциональных зависимостей между величинами. Обязательной к употреблению является Международная система единиц СИ.
1.1 КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ Трудности учета всех побочных явлений при измерениях, неполнота наших знаний, неточности измерительных приборов, приводят к неизбежным погрешностям измерений. Задача всех измерений заключается не в определении истинного значения, а в нахождении интервала, внутри которого находится истинное значение. Погрешности или ошибки измерений делятся на систематические, случайные, промахи. Систематические погрешности повторяются от измерения к измерению, причина их, как правило, известна и поэтому они могут быть учтены при измерениях (Например, стрелка амперметра при отсутствии тока не стоит на нуле). Случайные погрешности вызываются целым рядом неизвестных или случайным образом действующих причин. Их никогда не удается узнать полностью или устранить. Можно сказать, что эти погрешности обусловлены возможностями измерительных приборов, наших органов чувств и общими условиями измерений. Промахи – это ошибочные измерения или наблюдения. Результаты измерений в этих случаях не принимают во внимание при обработке.
2. СРЕДНЕЕ ЗНАЧЕНИЕ ИЗМЕРЯЕМОЙ ВЕЛИЧИНЫ При многократных измерениях какой-то величины, истинное значение которой a, проделывают n измерений. В результате получают ряд приближенных значений
Истинные абсолютные погрешности представим как
Тогда можем записать:
Складывая почленно, имеем:
Отсюда
Истинное значение а, выразится
Задача нахождения случайных погрешностей была решена Гауссом. В основе рассмотрения лежат две аксиомы: 1. Погрешности равной абсолютной величины и противоположных знаков равновероятны. 2. Чем больше абсолютная величина погрешности, тем она менее вероятна. Из первой аксиомы следует, что при бесконечном числе измерений (при
Но практически осуществить можно лишь конечное число измерений. И этого оказывается достаточно, так как на основе второй аксиомы маловероятны большие погрешности. Отсюда следует, что
3. ПОГРЕШНОСТИ ПРЯМЫХ ИЛИ НЕПОСРЕДСТВЕННЫХ ИЗМЕРЕНИЙ Если в результате измерения величины b получены значения
Абсолютные погрешности отдельных измерений
Результат измерения представляют так:
Расчеты проводятся с учетом правил приближенных вычислений. Относительная погрешность показывает, какую долю составляет абсолютная погрешность от среднего значения и выражается обычно в процентах
Наименьшая погрешность измерения не может быть меньше погрешности прибора. Последняя указывается в паспорте, либо за нее принимаем половину цены деления прибора. Если измерение проведено один раз или при многократных повторениях получается один и тот же результат, то погрешностью измерения считают погрешность прибора (по паспорту или классу точности прибора) или ее принимают равной половине цены наименьшего деления прибора. Класс точности прибора определяется максимальной погрешностью прибора, выраженной в процентах от полной величины шкалы. Например, класс точности 0,5 означает погрешность 0,5% при отклонении стрелки на всю шкалу. При отклонении стрелки на половину шкалы погрешность возрастает в два раза, при отклонении стрелки на треть шкалы – втрое.
4. ПОГРЕШНОСТИ КОСВЕННЫХ ИЗМЕРЕНИЙ При косвенных измерениях величину x находят как функцию непосредственно измеренных величин а, b, с. Абсолютные погрешности 1. Абсолютная погрешность суммы (разности) равна сумме абсолютных погрешностей слагаемых (уменьшаемого и вычитаемого)
2. Абсолютная погрешность произведения равна сумме произведений первого сомножителя на абсолютную погрешность второго и второго сомножителя на абсолютную погрешность первого
3. Абсолютная погрешность частного равна сумме произведений делимого на абсолютную погрешность делителя и делителя на абсолютную погрешность делимого, деленной на квадрат делителя
Относительная погрешность В математическом анализе показано, что
При этом x – есть какая-то функция Если заменить в полученном выражении все дифференциалы малыми конечными разностями
для конечных разностей
Если Формула для нахождения относительной погрешности будет записана так: (все члены берутся по абсолютной величине)
Для выражения в процентах нужно правую и левую части умножить на 100%. Эту формулу удобно использовать и для нахождения абсолютной погрешности. Действительно,
Результаты представляют так: Если функция x представляет сложную сумму или разность, то погрешности находятся для каждого члена отдельно, а затем суммируются. В тех случаях, когда в формулы для нахождения величины x входят физические или математические справочные величины, выраженные приближенными числами, их погрешностями считают половину единицы низшего ряда. Например,
4.1 СРЕДНЯЯ КВАДРАТИЧНАЯ ОШИБКА, КРИВАЯ ГАУССА, ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ Выше нами указано, что среднее арифметическое значение измеряемой величины равно
Средняя абсолютная погрешность
где n – число измерений. Часто, обрабатывая результаты, находят среднее квадратичное отклонение от среднего значения
По закону Гаусса функция распределения случайных величин (в нашем случае значений
и имеет вид
Точки Задача обработки серии измерений сводится к нахождению параметров кривой Зная функцию распределения случайных величин можно вычислить вероятности, с которыми истинное значение будет находиться в том или ином интервале значений. Этот интервал называется доверительным. Например,
Это значит, что истинное значение непосредственно измеренной величины с вероятностью около 0,7 находится в указанном интервале. С расширением интервала вероятность возрастает. При интервале Исходя из сказанного найденное значение величины
5. ПРИБОРЫ ДЛЯ ИЗМЕРЕНИЯ ЛИНЕЙНЫХ РАЗМЕРОВ И ПРАВИЛА ПОЛЬЗОВАНИЯ Для измерения линейных размеров тел используют мерные плиты, линейки, штангенциркули, катетометры, длинномеры, микромеры и т.д. Рассмотрим устройство штангенциркуля и микрометра. Штангенциркуль состоит из штанги с губкой. На штанге нанесена миллиметровая линейка (масштаб). По штанге движется рамка с другой губкой. На рамке находится дополнительная линейка – нониус. Нониус изготавливается так, что число его делений на одно меньше, чем совпадающее с ним число делений масштаба. Например,
Если губки штангенциркуля сжаты, то нуль нониуса и нуль масштаба совпадают. Если совместить штрих первого деления нониуса со штрихом первого деления масштаба, то между губками и будет расстояние 0,1 мм. Если совместить штрих второго деления нониуса со вторым штрихом линейки, то между губками будет 0,2 мм и т.д. При совмещении десятого деления нониуса с десятым деление линейки между губками расстояние будет 1 мм. Фактически, указанными действиями мы измеряли расстояние (размеры) 0,1 мм, 0,2 мм, 0,3 мм и т.д. Если у штангенциркуля 10 делений нониуса совпадают с 19 делениями линейки, то В этом случае расстояние между губками будет 0,1 мм при условии, что штрих первого деления нониуса совпадает со штрихом второго деления линейки. При измерении реального объекта его размеры определяют так: отсчитывают целое число миллиметров по линейке до нуля нониуса, затем смотрят, которое деление нониуса точно совпадает с делением линейки. Номер этого деления и показывает число десятых долей. За погрешность штангенциркуля принимается наименьшая измеряемая им величина. Микрометр состоит из полого стержня со шкалой, соединенного со скобой. В полом стержне помещается микровинт с прикрепленным к нему барабаном. Измеряемый предмет помещают между стержнем скобы и торцем микрометрического винта. По горизонтальной шкале на стержне ведут отсчет в миллиметрах, а самые доли отсчитывают по круговой шкале барабана.
6. ВЗВЕШИВАНИЕ НА ТЕХНИЧЕСКИХ ВЕСАХ ПРАВИЛА ВЗВЕШИВАНИЯ Взвешивание на расчетных технических весах позволяет определять массы тел путем сравнения их с эталонами. Для каждых весов указывается предельная масса, которая может быть определена. Весы – точный прибор, требующий осторожного обращения. Основная часть весов – равноплечное коромысло. К нему подвешиваются сережки с чашками. На концах коромысла укреплены регулирующие грузы, перемещая которые по винтам, можно осуществить регулировку весов. К центру коромысла прикреплена длинная стрелка, показывающая отклонение коромысла от равновесного положения. Установка платформы весов производится по отвесу с помощью опорных винтов. Для предохранения ребер призм от износа весы снабжены арретиром, который приводится в действие ручкой, расположенной на передней части платформы. В том случае, когда весами не пользуются или при изменении нагрузки, весы должны быть арретированы (остановлены, заперты). Чтобы не повредить весы и быстро получить правильные результаты нужно соблюдать правила пользования. 1. Разарретировать весы и убедиться, уравновешены ли они. Если стрелка выходит за пределы шкалы, то весы нужно арретировать и переместить регулирующие грузы. 2. Если колебания стрелки происходят в пределах шкалы, то следует по ее отклонениям определить нулевую точку. 3. Определить цену деления шкалы. Для этого на правую чашку весов кладут известный малый перегрузок (равновесок) и определяют, на сколько делений отклоняется стрелка от найденной нулевой точки. 4. Арретировать весы, положить тело на левую чашку, а гири на правую. 5. Плавно открывая арретир, убедиться, уравновешивают ли гири тело. Если нет, то снова арретировать и прибавить или убавить массу гирь. Так действовать до тех пор, пока стрелка при открытом арретире не будет колебаться в пределах шкалы. 6. Если не удается привести стрелку в найденное нулевое положение, то нужно учесть отклонение и, зная цену деления, определить окончательный результат взвешивания. 7. Нельзя взвешивать тела большей массы, чем указано на весах. 8. Разновес брать пинцетом, после снятия с весов класть в футляр на свое место. 9. Подготовку весов к работе должен проводить лаборант. 7. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Измерить линейные размеры некоторых тел 2. Определить массы тел на рычажных весах m (прямые измерения) и вычислить плотности этих тел 3. Вычислить абсолютные и относительные погрешности прямых и косвенных измерений и представить результаты измерений
4. Результаты измерений и расчетов занести в таблицу.
Таблица
ТРЕБОВАНИЯ К ОТЧЕТУ Отчет должен содержать краткие сведения об измерениях, нахождении средних значений, нахождении абсолютных и относительных погрешностей и результаты измерений и вычислений.
8. КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Что такое измерение? Какие измерения бывают? 2. Как находят погрешности прямых и косвенных измерений? 3. Какова наименьшая погрешность при прямых измерениях? При косвенных измерениях?
9. ЛИТЕРАТУРА 1. Лабораторный практикум по физике. Под ред. А. С. Ахматова. М., Высшая школа, 1980.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
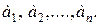
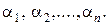
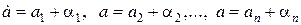
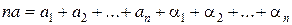
 ,
, среднее арифметическое отдельных измерений.
среднее арифметическое отдельных измерений.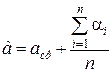
 истинная абсолютная погрешность, которая остается неизвестной.
истинная абсолютная погрешность, которая остается неизвестной. )
) и тогда
и тогда 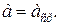
 многих измерений, и встает задача оценить степень приближения среднего значения к истинному.
многих измерений, и встает задача оценить степень приближения среднего значения к истинному. то среднее арифметическое значение
то среднее арифметическое значение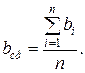
 равны по модулю разностям среднего значения
равны по модулю разностям среднего значения 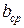 и результатов отдельных измерений
и результатов отдельных измерений 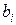
 ,
,  ,…,
,…, 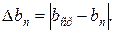
 средняя абсолютная погрешность измерений.
средняя абсолютная погрешность измерений.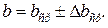
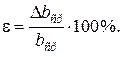
 непосредственных измерений обуславливают абсолютную погрешность
непосредственных измерений обуславливают абсолютную погрешность  При нахождении
При нахождении  используют следующие теоремы:
используют следующие теоремы:
 ,
, 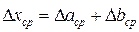

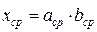 ,
, 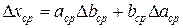

 ,
, 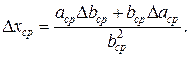
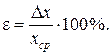
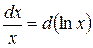
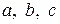 и т. д. в явном виде, и, следовательно, можно вычислить ее дифференциал от логарифма, который будет содержать
и т. д. в явном виде, и, следовательно, можно вычислить ее дифференциал от логарифма, который будет содержать  и т. д.
и т. д. и т.д., то получим формулу для относительной погрешности
и т.д., то получим формулу для относительной погрешности
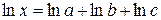
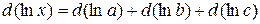
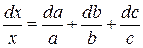
 .
. есть абсолютные погрешности при непосредственных измерениях а, b, с, то
есть абсолютные погрешности при непосредственных измерениях а, b, с, то  .
. .
. .
.
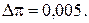
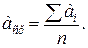
 ,
,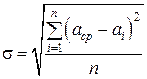
 ) записывается
) записывается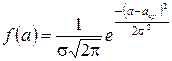

 соответствуют точкам перегиба на кривой Гаусса.
соответствуют точкам перегиба на кривой Гаусса. и
и  .
. <
< 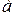 <
< 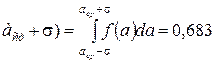
 Р=0,955.
Р=0,955. (с вероятностью 0,683)
(с вероятностью 0,683) (с вероятностью 0,955).
(с вероятностью 0,955).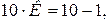
 , где К – цена деления нониуса.
, где К – цена деления нониуса. наименьшая величина, измеряемая штангенциркулем.
наименьшая величина, измеряемая штангенциркулем.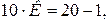
 , т.е. цена деления нониуса другая, а наименьшая величина, измеряемая штангенциркулем
, т.е. цена деления нониуса другая, а наименьшая величина, измеряемая штангенциркулем  .
. (прямые измерения) и вычислить их объемы
(прямые измерения) и вычислить их объемы 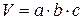 или
или 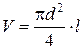 (косвенные измерения).
(косвенные измерения). (косвенные измерения).
(косвенные измерения).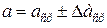

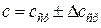

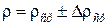 .
.