
|
|
Линейная регрессия и метод наименьших квадратов.БИОСТАТИСТИЧЕСКИЙ АНАЛИЗ доц. Е.Б. Яровая для студентов 3-6 курсов и аспирантов факультета фундаментальной медицины Курс рассчитан на слушателей, планирующих использование статистических методов в медико-биологических исследованиях. Изложение ориентировано на применение пакетов прикладных статистических программ и проиллюстрировано примерами из области биологии и медицины. Осенний семестр. Первая часть курса включает основные понятия теории вероятностей и математической статистики, а также наиболее распространенные методы статистической обработки данных. Введение. 1. Задачи прикладной статистики. 2. Статистика в клинической практике. Основные понятия теории вероятностей. 1. Вероятностная модель эксперимента с дискретным числом исходов. Примеры. 2. События и их вероятности. 3. Случайные величины. Функции распределения. 4. Характеристики распределения: математическое ожидание, дисперсия, медиана, мода, асимметрия, эксцисс, моменты, квантили. 5. Независимые и зависимые случайные величины. 6. Понятие о совместной функции распределения случайных величин. Законы распределения вероятностей, Распространенные в практике статистических исследований 1. Дискретные распределения. · 1.1. Биномиальное распределение. · 1.2. Распределение Пуассона. 2. Непрерывные распределения. · 2.1. Равномерное распределение. · 2.2. Экспоненциальное распределение. · 2.3. Нормальное распределение. · 2.4. Распределения, связанные с нормальным. 3. Многомерное нормальное распределение. Основные результаты теории вероятностей. 1. Закон больших чисел. 2. Центральная предельная теорема. Выборочные оценки. 1. Случайный выбор. · 1.1. Генеральная совокупность и выборка. · 1.2. Репрезентативность выборки. · 1.3. Основные способы организации выборки. 2. Эмпирическая функция распределения. Гистограмма. 3. Оценивание параметров распределения по выборке. Свойства оценок: несмещенность, состоятельность, эффективность. Примеры. 4. Выборочные характеристики. Выборочное среднее и выборочная дисперсия, их несмещенность. 5. Ранги и ранжирование. Доверительные интервалы. 1. Понятие доверительного интервала. Метод построения доверительных интервалов. 2. Доверительные интервалы для параметра a в случае выборки из нормального распределения 3. Доверительные интервалы для параметра Проверка статистических гипотез. 1. Понятие статистической гипотезы. Проверка гипотез. Критическое множество. Простые и сложные гипотезы. Ошибка 1 рода. 2. Теорема Пирсона. Непараметрический критерий согласия Пирсона. Проверка гипотезы 3. Понятие о проверке основной простой гипотезы Обработка данных. Элементарные статистические выводы. Примеры. 1. Выбор статистической модели. · 1.1. Параметрические и непараметрические критерии. · 1.2. Проверка нормальности. Критерии согласия. 2. Анализ парных наблюдений. · 2.1. Парный t-критерий. · 2.2. Критерий Уилкоксона. 3. Анализ двух независимых выборок. · 3.1. Непарный t-критерий (случаи равных и неравных дисперсий). · 3.2. Критерий Манна-Уитни. 4. Таблицы сопряженности признаков. · 4.1. Точный критерий Фишера для таблиц сопряженности признаков · 4.2. Критерий 5. Анализ повторных измерений. · 5.1. Дисперсионный анализ повторных измерений с использованием параметрических критериев. · 5.2. Ранговый критерий Фридмана. 6. Анализ нескольких независимых выборок. · 6.1. Дисперсионный анализ по одному признаку для проверки равенства средних. · 6.2. Непараметрический дисперсионный анализ по одному признаку с применением критерия Краскала-Уоллиса. · 6.3. Множественный t-критерий, критерии Шеффе и Тьюки. Линейная регрессия и метод наименьших квадратов. 1. Метод наименьших квадратов. 2. Критерий значимости линии регрессии. 3. Точечные оценки, доверительные интервалы и проверка гипотез o параметрах линии регрессии. 4. Сравнение двух простых линейных регрессионных уравнений. 5. Множественная линейная регрессия, множественная и частная корреляции. 6. Пошаговая регрессия. 7. Нелинейная регрессия. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
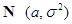 : (a) при известном
: (a) при известном 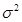 ; (b) при неизвестном
; (b) при неизвестном 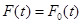 .
.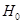 :
:  при альтернативе
при альтернативе  :
: 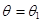 . Ошибки 1-го и 2-го рода. Критерий, основанный на отношении правдоподобия.
. Ошибки 1-го и 2-го рода. Критерий, основанный на отношении правдоподобия. .
.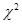 .
.