
|
|
Состав и основные параметры влажного воздухаСмесь сухой части воздуха с некоторым количеством водяных паров называется влажным воздухом. Атмосферный воздух также представляет собой влажный воздух или воздушно-паровую смесь. Сухая часть влажного воздуха (без водяных паров), в свою очередь, является смесью нескольких типовых газов, а также может содержать характерные для данного района компоненты. Типовой состав сухой части атмосферного воздуха приведен в табл. 2.1.
Таблица 2.1 Типовой состав сухой части воздуха
С достаточной для технических расчётов точностью, рассматривая воздух как бинарную смесь сухой части и водяного пара, можно считать, что как отдельные компоненты (сухой воздух, водяной пар), так и их смесь (влажный воздух) подчиняются законам идеальных газов. Тогда, на основании уравнения Клапейрона-Менделеева, можно записать: для сухого воздуха
для водяного пара
В выражениях (2.1) и (2.2), соответственно: Газовая постоянная может быть определена из универсальной газовой постоянной и составляет соответственно: для сухого воздуха
для водяного пара
В выражениях (2.3) и (2.4) соответственно: Представляют практический интерес численные значения плотности сухого воздуха и водяного пара при нормальных условиях, т.е. при барометрическом давлении для сухого воздуха
для водяного пара
В выражениях (2.5) и (2.6) соответственно: 0,76 - барометрическое давление, м рт.ст.; 13600 - плотность ртути, кг/м3; 9,81 – ускорение свободного падения, м/с2; 273 - абсолютная температура по шкале Кельвина, соответствующая температуре 0 °С. Барометрическое давление атмосферного воздуха в соответствии с законом Дальтона равно сумме парциальных давлений сухой части воздуха и водяного пара
Смесь, которая состоит из сухого воздуха и перегретого водяного пара, называют ненасыщенным влажным воздухом, а смесь, состоящую из сухого воздуха и насыщенного водяного пара, насыщенным влажным воздухом. Абсолютной влажностью воздуха
где Абсолютная влажность в насыщенном состоянии при данной температуре называется влагоёмкостью воздуха
где Относительная влажность воздуха представляет собой отношение концентрации водяного пара в ненасыщенном воздухе к концентрации водяного пара в насыщенном состоянии при одинаковых температурах и давлениях. Величина относительной влажности определяется в долях или процентах и может быть выражена
Парциальное давление водяного пара в насыщенном состоянии при данной температуре может быть определено по справочным таблицам, с помощью специальной диаграммы или аналитически по известным эмпирическим зависимостям. Влагосодержание влажного воздуха
Подставив в выражение (2.11) значения
Выразив величину парциального давления сухого воздуха
Если массу водяного пара выразить в кг, то влагосодержание принято обозначать буквой
Теплосодержание влажного воздуха представляют как сумму теплосодержания сухой части воздуха и водяного пара
При этом теплосодержание сухой части воздуха при известной температуре
где Теплосодержание водяного пара при известной температуре
где Для практических инженерных расчётов можно приблизительно принять:
1.2. Принципы построения
Л. К. Рамзин, используя выражение (2.18), предложил Общий вид диаграммы приведен на рис.1.1. По оси ординат в соответствующем масштабе откладывают значения теплосодержаний. Через полученные точки проводятся линии постоянных теплосодержаний На полученной таким образом сетке, состоящей из параллелограммов, строятся линии изотерм Анализ выражения (2.18) показывает, что при Соединив плавной кривой точки, соответствующие состоянию полного насыщения влажного воздуха при различных значениях температур, получим линию относительной влажности Для построения кривых относительной влажности при других значениях
где Для построения линии парциального давления пара с правой стороны диаграммы на линии, параллельной оси ординат, наносится шкала парциальных давлений, начиная с На вертикалях по линии Кроме этого, на поле
1.3. Угловой коэффициент и изображение основных процессов изменения состояния влажного воздуха в Изменение состояния влажного воздуха характеризуется термовлажностным соотношением или угловым коэффициентом. Осуществляемый процесс в Рассмотрим произвольный процесс, изображённый на рис. 2.2.
Рис. 2.2. Графическая интерпретация выражения углового коэффициента.
Предположим, что начальное состояние влажного воздуха характеризуется точкой М1 с параметрами
Тригонометрическое выражение углового коэффициента состоит в следующем. Проведя через точку М1 линию
Применив теорему синусов, выражение (2.21) можно записать в следующем виде:
Так как
Подставив (2.23) в (2.22), окончательно можно записать
Наиболее характерные процессы изменения состояния влажного воздуха и изображение их на Процесс 1-2 характеризуется нагревом влажного воздуха при постоянном влагосодержании
Процесс 1-3 характеризуется нагревом влажного воздуха и его дополнительным увлажнением, т.е. протекает при одновременном поглощении теплоты и влаги. Величина углового коэффициента при
Процесс 1-4 протекает при постоянном теплосодержании
Рис. 2.3. Характерные процессы изменения состояния влажного воздуха Процесс 1-5 характеризуется охлаждением влажного воздуха при постоянном влагосодержании
Процесс 1-6 характеризуется охлаждением воздуха и его осушением, т.е. протекает при одновременном выделении теплоты и влаги. Величина углового коэффициента при

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 или зная, что
или зная, что 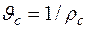
 , откуда
, откуда 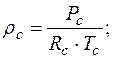 (2.1)
(2.1)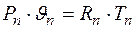 или зная, что
или зная, что 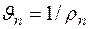
 , откуда
, откуда 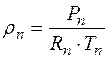 . (2.2)
. (2.2)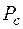 и
и  ,
, 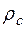 и
и 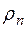 ,
,  и
и 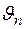 ,
,  и
и 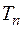 ,
, 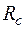 и
и 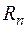 - парциальное давление, плотность, удельный объём, температура и газовая постоянная сухого воздуха и водяного пара.
- парциальное давление, плотность, удельный объём, температура и газовая постоянная сухого воздуха и водяного пара.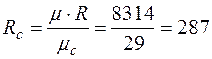 , Дж/(кг К); (2.3)
, Дж/(кг К); (2.3) , Дж/(кг К). (2.4)
, Дж/(кг К). (2.4)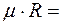 8314 Дж/(кмоль·К) - универсальная газовая постоянная;
8314 Дж/(кмоль·К) - универсальная газовая постоянная;  кг/кмоль и
кг/кмоль и 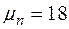 кг/кмоль - молекулярная масса сухого воздуха и водяного пара.
кг/кмоль - молекулярная масса сухого воздуха и водяного пара.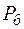 = 760 мм.рт.ст. и температуре t = 0 °С. Расчёт производится на основании выражений (2.1) и (2.2) и их значения составляют:
= 760 мм.рт.ст. и температуре t = 0 °С. Расчёт производится на основании выражений (2.1) и (2.2) и их значения составляют: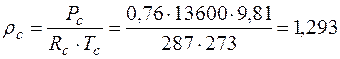 , кг/м3; (2.5)
, кг/м3; (2.5) , кг/м3 . (2.6)
, кг/м3 . (2.6)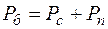 . (2.7)
. (2.7)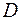 называется масса водяного пара, содержащаяся в 1 м3 влажного воздуха
называется масса водяного пара, содержащаяся в 1 м3 влажного воздуха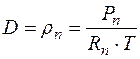 , кг/м3 , (2.8)
, кг/м3 , (2.8)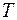 - абсолютная температура влажного воздуха, К.
- абсолютная температура влажного воздуха, К.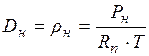 , кг/м3 , (2.9)
, кг/м3 , (2.9) - плотность водяного пара в насыщенном состоянии, кг/м3;
- плотность водяного пара в насыщенном состоянии, кг/м3;  - парциальное давление водяного пара в насыщенном состоянии (упругость водяных паров) , Па.
- парциальное давление водяного пара в насыщенном состоянии (упругость водяных паров) , Па.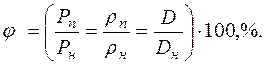 (2.10)
(2.10) представляет собой отношение массы водяного пара к единице массы сухого воздуха, содержащегося в смеси
представляет собой отношение массы водяного пара к единице массы сухого воздуха, содержащегося в смеси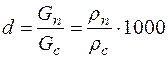 , г/кг . (2.11)
, г/кг . (2.11) , г/кг. (2.12)
, г/кг. (2.12)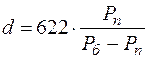 , г/кг . (2.13)
, г/кг . (2.13)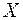 , и тогда выражение (2.13) принимает вид
, и тогда выражение (2.13) принимает вид , кг/кг . (2.14)
, кг/кг . (2.14)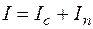 , кДж/кг . (2.15)
, кДж/кг . (2.15)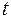 , °С можно выразить
, °С можно выразить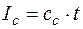 , кДж/кг , (2.16)
, кДж/кг , (2.16) - теплоёмкость сухого воздуха, кДж/(кг °С).
- теплоёмкость сухого воздуха, кДж/(кг °С). , кДж/кг , (2.17)
, кДж/кг , (2.17)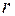 - скрытая теплота парообразования водяного пара, кДж/кг; Сп- теплоёмкость водяного пара, кДж/(кг °С).
- скрытая теплота парообразования водяного пара, кДж/кг; Сп- теплоёмкость водяного пара, кДж/(кг °С).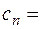 1,8 кДж/(кг °С);
1,8 кДж/(кг °С); 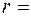 2500 кДж/кг. Тогда выражение (1.17) можно записать
2500 кДж/кг. Тогда выражение (1.17) можно записать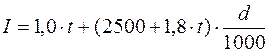 , кДж/кг . (2.18)
, кДж/кг . (2.18)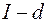 диаграммы влажного воздуха
диаграммы влажного воздуха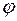 ,
, 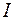 при заданном барометрическом давлении.
при заданном барометрическом давлении.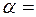 135°. На оси абсцисс в соответствующем масштабе откладываются значения влагосодержаний
135°. На оси абсцисс в соответствующем масштабе откладываются значения влагосодержаний .
.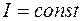 под углом
под углом  = 135° к линиям
= 135° к линиям 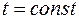 и кривые постоянных относительных влажностей
и кривые постоянных относительных влажностей 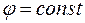 .
.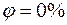 и
и 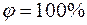 . При соответствующих значениях температуры по уравнениям (2.18) и (2.13) для принятого барометрического давления
. При соответствующих значениях температуры по уравнениям (2.18) и (2.13) для принятого барометрического давления 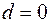 ), крайние правые точки (при
), крайние правые точки (при  , (2.19)
, (2.19)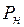 - парциальное давление водяного пара в насыщенном состоянии при данной температуре, определяемое по справочным таблицам.
- парциальное давление водяного пара в насыщенном состоянии при данной температуре, определяемое по справочным таблицам. до величины возможного значения
до величины возможного значения 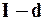 диаграмме
диаграмме
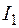 и
и  , а конечное - точкой М2 с параметрами
, а конечное - точкой М2 с параметрами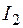 и
и 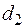 . Тогда отношение разности теплосодержаний к разности влагосодержаний в указанных точках обозначается
. Тогда отношение разности теплосодержаний к разности влагосодержаний в указанных точках обозначается  и называется угловым коэффициентом
и называется угловым коэффициентом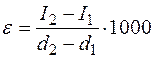 , кДж/кг влаги . (2.20)
, кДж/кг влаги . (2.20)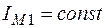 , а через точку М2 линию
, а через точку М2 линию 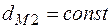 , получим треугольникМ1М2К. В этом случае величину углового коэффициента можно выразить
, получим треугольникМ1М2К. В этом случае величину углового коэффициента можно выразить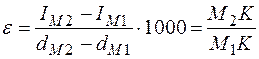 . (2.21)
. (2.21)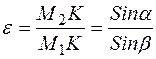 . (2.22)
. (2.22) 135° , то угол
135° , то угол 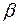 можно выразить через угол
можно выразить через угол  . (2.23)
. (2.23)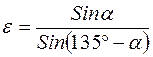 . (2.24)
. (2.24)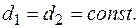 Величина углового коэффициента при
Величина углового коэффициента при  составит
составит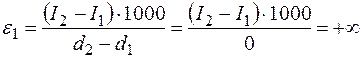 . (2.25)
. (2.25) и
и 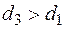 составит
составит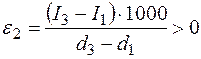 . (2.26)
. (2.26)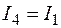 с одновременным поглощением влаги
с одновременным поглощением влаги 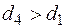 . Луч этого процесса проходит по линии
. Луч этого процесса проходит по линии 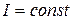 , а сам процесс называется адиабатическим. Величина углового коэффициента составит
, а сам процесс называется адиабатическим. Величина углового коэффициента составит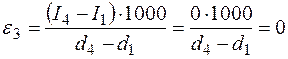 . (2.27)
. (2.27)
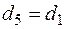 . Величина углового коэффициента при
. Величина углового коэффициента при 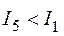 составит
составит . (2.28)
. (2.28) и
и  составит
составит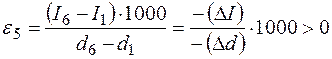 . (2.29)
. (2.29)