
|
|
Знакопеременные, знакопостоянные и знакоопределенные квадратичные формы.Линейные пространства. Замена базиса. Линейные системы. Критерий совместности системы (теорема Кронекера-Капелли). 1.1. Закон преобразования координат вектора при переходе к новому базису. Матрица перехода от старого базиса к новому базису, ее невырожденность. 1.2. Повторение основных понятий, терминов и методов решений, связанных с линейными системами ( совместность, несовместность, эквивалентные системы, элементарные преобразования, однородные и неоднородные системы, вырожденные и невырожденные системы, правило Крамера, матричный метод, метод Гаусса). 1.3. Критерий совместности линейной системы (теорема Кронекера-Капелли). Условия единственности и не единственности решения. Однородные и неоднородная системы линейных уравнений. 2.1. Однородная система линейных уравнений, ее совместность. 2.2. Теорема о структуре общего решения линейной однородной системы (множество всех решений - линейное пространство). Базис (фундаментальная система решений) и размерность пространства решений линейной однородной системы. 2.3. Неоднородная система линейных уравнений, соответствующая ей однородная система. Теорема о структуре совместной линейной неоднородной системы. Отображения множеств. Линейные операторы и их матрицы. 3.1. Отображения множеств. Образ и прообраз. Однозначное и взаимно однозначное отображения, примеры. Композиция отображений. Обратное отображение. Линейное отображение множеств. 3.2. Линейный оператор, его свойства, примеры линейных операторов. 3.3. Матричная запись действия линейного оператора в заданном базисе. Матрица линейного оператора и ее преобразование при переходе к новому базису. Действия с линейными операторами. 4.1. Умножение линейного оператора на число, сложение линейных операторов, перемножение линейных операторов. Связь указанных действий с соответствующими операциями над матрицами линейных операторов. 4.2. Условие существования обратного отображения к линейному оператору, его свойства. Матрица обратного оператора, ее нахождение по матрице оператора. Критерий обратимости линейного оператора в терминах его матрицы. 4.3. Ядро и образ линейного оператора, их свойства. Ранг и дефект линейного оператора. Критерий обратимости линейного оператора в терминах его ядра, образа, ранга, дефекта. Собственные значения и собственные векторы линейного оператора. 5.1. Определение собственного вектора и собственного значения линейного оператора, их геометрический смысл. Главные направления линейного оператора. Нахождение собственных векторов и собственных значений на примере оператора 5.2. Линейная независимость собственных векторов с различными собственными значениями. Нахождение собственных значений и собственных векторов линейного оператора. 6.1. Характеристическая матрица, характеристический многочлен и характеристическое уравнение. Инвариантность характеристического многочлена и определителя матрицы линейного оператора. 6.2. Нахождение собственных значений из характеристического уравнения и собственных векторов из однородной системы с характеристической матрицей. Линейный оператор простого типа. 7.1. Определение линейного оператора простого типа, диагонализуемость его матрицы. Достаточные условия оператора простого типа. 7.2. Геометрический смысл определителя матрицы линейного оператора в пространстве геометрических векторов. Линейные, билинейные и квадратичные функции в линейном пространстве. 8.1. Линейная функция в линейном пространстве и ее представление в заданном базисе. 8.2. Билинейная функция в линейном пространстве и соответствующая ей билинейная форма в заданном базисе. Векторно-матричная запись билинейной формы. Матрица билинейной формы, закон ее изменения при переходе к новому базису и инвариантность ранга этой матрицы. 8.3. Квадратичная функция в линейном пространстве. Симметричные билинейные функции и соответствующие им квадратичные функции. Квадратичные функции и соответствующие им квадратичные формы. Матрица квадратичной формы и закон ее изменения при переходе к новому базису. Приведение квадратичной формы к каноническому и нормальному виду. 9.1. Канонический и нормальный вид квадратичной формы. 9.2. Метод Лагранжа приведения квадратичной формы к каноническому и нормальному виду. 9.3. Положительный и отрицательный индексы, ранг квадратичной формы. Закон инерции. Три инварианта квадратичной формы. Знакопеременные, знакопостоянные и знакоопределенные квадратичные формы. 10.1. Знакопеременные, знакопостоянные квадратичные формы (определения, примеры). Их канонический и нормальный вид, индексы и ранг. 10.2. Знакоопределенные (положительно и отрицательно определенные) квадратичные формы. Их канонический и нормальный вид. Индексы и ранг знакоопределенной формы. 10.3. Критерий Сильвестра положительной (отрицательной) определенности квадратичной формы. Евклидово пространство. 11.1. Определение евклидова пространства. Евклидово скалярное произведение. Примеры евклидовых пространств. 11.2. Неравенство Коши-Буняковского. 11.3. Длина вектора и угол между векторами в евклидовом пространстве. 11.4. Неравенство треугольника. Матрица Грама. 12.1. Координатная и векторно-матричная запись скалярного произведения в заданном базисе. Матрица Грама и ее свойства. Примеры матриц Грама. 12.2. Преобразование матрицы Грама при переходе к новому базису. 12.3. Нахождение матрицы Грама скалярного произведения в базисе Ортонормированный базис. 13.1. Ортогональная система векторов, ее линейная независимость. 13.2. Ортогональный и ортонормированный базисы. Матрица Грама, запись скалярного произведения векторов и длин векторов в этих базисах. Теорема Пифагора в произвольном и ортонормированном базисах евклидова пространства. 13.3. Метод ортогонализации базиса. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 зеркального отражения векторов от заданной плоскости
зеркального отражения векторов от заданной плоскости 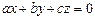 .
. пространства
пространства  геометрических векторов в случае, когда скалярное произведение в каноническом (ортонормированном) базисе
геометрических векторов в случае, когда скалярное произведение в каноническом (ортонормированном) базисе 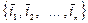 этого пространства задается стандартным образом.
этого пространства задается стандартным образом.