|
|
Определение проходной осадки суднаПЛАВАНИЕ НА МЕЛКОВОДЬЕ И В УЗКОСТЯХ Движение судна на мелководье существенно отличается от условий плавания на глубокой воде. Это связано с перераспределением гидродинамических давлений на корпусе судна из-за: 1) изменения структуры волнообразования; 2) уменьшения проходного сечения для тока жидкости из-за наличия дна; 3) уменьшения проходного сечения для тока жидкости из-за наличия внешних стенок (при плавании в каналах); 4) изменения характера работы вито-рулевого комплекса и др. Теоретические исследования изменения поля давлений и гидродинамических сил, действующих на корпус судна при движении в условиях мелководья и стесненного фарватера делятся на два направления: - гидравлическое; - гидродинамическое. В соответствии с первым направлением, которое развивается уже более 80 лет используется физическая модель движения судна, которая дает возможность получить приближенное решение задачи путем применения уравнения Бернулли совместно с уравнением неразрывности жидкости. Пусть судно движется с постоянной скоростью V по мелководному участку параллельно стенкам канала (пролива). Жидкость считается идеальной и несжимаемой, а ее возмущенное движение – потенциальным. Введем и рассмотрим прямоугольную систему координат Оxyz, жестко связанную с судном, начало которой находится в точке пересечения плоскости мидель-шпангоута, диаметральной плоскости и плоскости действующей ватерлинии судна. Обратим движение, наложив на судно равномерный поток, движущийся со скоростью V в отрицательном направлении оси Х. В соответствии с уравнением Бернулли, полная энергия материальной частицы движущейся жидкости Мi есть величина постоянная и определяется выражением:
В соответствии с уравнением неразрывности для установившегося одномерного движения идеальной жидкости количество жидкости перетекающей через сечения S0 и S1 за время Δt есть величина постоянная и которая определяется выражением:
Определяя из выражения (2.) значение скорости V1 после подстановки значения V1 в уравнение (1.), получим:
с учетом подстановки
Левая часть выражения (4.) определяет величину динамической просадки судна из-за уменьшения сечения S1 для тока жидкости. Анализируя выражение (4.) необходимо отметить, что величина динамической просадки какой-либо точки судна или рассматриваемого сечения корпуса судна, квадратично зависит от скорости движения и соотношения площадей сечения В первом приближении конфигурацию, размеры и границы сечений можно связать с такими параметрами как: - глубина водной акватории H; - ширина судна Вс; - ширина канала Вк; - статическая осадка судна на глубокой воде dгл и др. Анализируя работы по исследованию гидравлических процессов [15], следует отметить, что методы основаны на рассмотрении одномерного течения идеальной жидкости базируются на ряде существенных упрощающих допущений. Так в вышеприведенном примере к таким допущениям следует отнести: 1) неучет влияния свободной поверхности; 2) неучет влияния системы волнообразования; 3) отсутствие строгой теории по учету формы корпуса; 4) потенциальное движение идеальной жидкости и др. В работе [20], на основе обобщения различных методик по определению величины просадки, предлагается простая зависимость для определения безопасного запаса воды под килем:
где
В результате обобщения различных формул, графиков, номограмм, рассчитаны коэффициенты аппроксимации с использованием метода наименьших квадратов
На рис. 1 представлены графики величины просадки судна в зависимости от длины корпуса судна и скорости установившегося движения. Анализ показывает, что для диапазона длин 250-300 м и скоростей движения 9-11 уз – величина просадки находится в пределах от 1,8 до 2,5 метров.
Рис. 1. Максимальная просадка судна
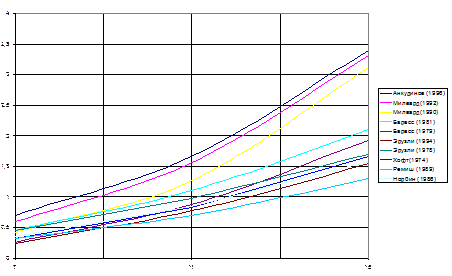
Рис. 2. Величина просадки судна по зарубежным методикам На рис. 2. представлены расчеты величины просадки по некоторым зарубежным методикам. В качестве расчетного принято судно с размерениями: L = 250 м, Т=18 м, Н = 26 м. Анализ рис. 2. показывает, что для диапазона скоростей 10-11 уз, величина просадки находится в пределах 0,7-1,7 метра.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , (1.)
, (1.) . (2.)
. (2.)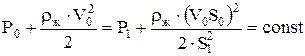 , (3.)
, (3.) преобразуем уравнение (3.) к виду:
преобразуем уравнение (3.) к виду: . (4.)
. (4.)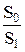 , через которые осуществляется ток жидкости.
, через которые осуществляется ток жидкости.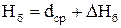 , (5.)
, (5.)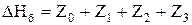
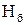
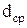


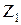
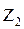

 , (6.)
, (6.)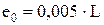 ,
,  ,
, 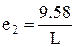 ,
,  .
.