
|
|
Гипотеза о равенстве вектора средних значений постоянному векторуЛабораторная работа №3 Тема: Проверка статистических гипотез
Проверка гипотез. Проверка статистической гипотезы предполагает наличие выборочной совокупности данных, которая параметрически (своей функцией распределения) сравнивается с генеральной совокупностью или другой выборкой. При проверке статистических гипотез используется понятие нулевой (прямой) и альтернативной (обратной, конкурирующей) гипотез. Прямая гипотеза (H0) является основной и обычно содержит утверждение об отсутствии различий между сравниваемыми величинами. Альтернативная гипотеза (Н1) представляется конкурирующей по отношению к нулевой и принимается после того, как отвергнута основная. Суждения об истинности или ложности статистической гипотезы строятся на основе критериальной (тестовой) проверки. Существуют статистические критерии, отражающие результаты сравнений и принимающие наблюдаемые значения по выборочным данным, а также критерии критических значений, установленные теоретическим путем. В ходе сопоставления критериальных величин выясняется: можно принимать или следует отвергнуть нулевую гипотезу. Если наблюдаемое значение критерия не превышает критического, то, по крайней мере, теоретически отсутствуют основания, чтобы отвергнуть прямую (нулевую) гипотезу. В противоположном случае целесообразно предположить справедливость альтернативной гипотезы Н1. Критериальная проверка статистических гипотез допускает определенную вероятность ошибки в выводах. При этом разделяют вероятность ошибки первого рода В экономических и социологических исследованиях из двух вероятностных характеристик ошибок, которые допускаются при проверке гипотез ( Критериальная проверка гипотезы, в сущности, означает сравнительную характеристику параметрических значений или самого распределения случайной величины. Так, значения нормально распределенной величины, расположенные в непосредственной близости от центра распределения (математического ожидания В многомерном случае используются те же статистические критерии соответствия, что и в одномерном, но они изменяются с учетом многовекторной природы случайной величины. Чаще всего это критерии для проверки параметрических гипотез: t-Стьюдента, F-Фишера, проверки непараметрических гипотез ‑
Гипотеза о равенстве вектора средних значений постоянному вектору В многомерном случае имеем дело c m – числом выборочных средних, т.е. вектором средних значений: Согласно двум приведенным гипотезам все Наблюдаемое значение T2-критериявычисляется по формуле:
T2 ‑ критерий известен как критерий Хотеллинга Наблюденное значение
В формуле
В многомерном статистическом анализе проверяется гипотеза о равенстве векторов средних значений для двух выборок имеет вид:
при этом конкурирующая гипотеза может быть записана следующим образом:
или в векторной форме:
Наблюдаемое значение T2-критериявычисляется по формуле:
где
Критические значения для Т2 находятся по формуле, включающей квантиль F-распределения Фишера-Снедекора, определяемый при заданном уровне значимости
При Расчет частных критериев
где Для частных оценок различий средних значений критические величины определяются формулой:
Сравнение ковариационных матриц, отражающих взаимосвязи изучаемых признаков, открывает возможность дополнить и уточнить гипотетические предположения относительно самих признаков. Это приобретает особенное значение, если принять во внимание, что даже специфические индивидуальные признаковые характеристики могут совпадать случайно. Нулевая гипотеза о равенстве дисперсий отклоняется, если Формула расчета статистики где параметры b и
где n – объем выборки; m ‑ число признаков, представляющих многомерную выборочную совокупность;
Величина W-критерия сравнивается с
Задания
№1. На частном предприятии с численностью работников 70–а человек средний уровень выработки одного рабочего составляет 500+10a деталей в день при среднеквадратическом отклонении 16+a деталей. С целью корректировки среднего нормативного уровня выработки в сторону повышения администрацией была отобрана группа наиболее подготовленных рабочих и по ним установлен средний уровень выработки 580+9a деталей. Можно ли вводить новый нормативный уровень выработки, не опасаясь конфликтов с рабочими? Решить задачу при α=0,05 (a – номер варианта).
№2. Чтобы оценить производственную эффективность предложенной к внедрению технологии, проведена проверка качества продукции, выпущенной на старой и новой автоматических линиях, при этом получены следующие данные об удельном весе продукции высшего качества, в %:
Установить, действительно ли новая линия, налаженная на передовую технологию, позволяет получать более высокий уровень качества продукции. Решить задачу при α=0,005 (a – номер варианта).
№3. Для оценки существенности воздействия состояния окружающей среды на здоровье людей в районе с неблагоприятной экологической обстановкой проведены обследования 12 отобранных случайных групп населения и получены данные, представленные в таблице. Известно, что средний по стране уровень продолжительности жизни составляет 69 лет, средняя заболеваемость онкологическими заболеваниями составляет 580 человек на 100 тыс. человек, средний уровень младенческой смертности равен 12%. Определить, действительно ли экологическая обстановка оказывает негативное влияние на уровень здоровья. Найти доверительные интервалы по первому и второму походам. Решить задачу при α=0,01 (a – номер варианта).
№4. Проверить существенность различий уровня эффективности работы предприятий двух отраслей А и Б по следующим данным (проверить гипотезы о равенстве векторов средних значений и равенстве ковариационных матриц):
Решить задачу при α=0,1.
№5. Проверить, оказывает ли влияние на значения показателей муниципальных районов Вологодской области наличие рядом расположенных городов.Проверку проводить для следующихе факторов, представленных в таблице.
Районы, расположенные рядом с городами: Великоустюгский, Вологодский, Грязовецкий, Сокольский, Череповецкий и Шекснинский. Проверить гипотезы о равенстве средних значений в группах. Решить задачу при α=0,005.
№6. Сравните вектора средних и ковариационные матрицы показателей Вологодской области с среднероссийскими значениями. Найти доверительные интервалы по первому и второму подходам. Решить задачу при α=0,01.
№7. Проверить существенность различий показателей 1998 и 2007 годов:
Решить задачу при α=0,1.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ‑ отвергнуть нулевую гипотезу, когда она справедлива, и второго рода
‑ отвергнуть нулевую гипотезу, когда она справедлива, и второго рода 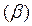 ‑ принять нулевую гипотезу, когда она ложна.
‑ принять нулевую гипотезу, когда она ложна. и
и  ) обычно используется
) обычно используется  ) равную: 0,99; 0,95; 0,90.
) равную: 0,99; 0,95; 0,90. ) и априорно имеющие более высокую степень (вероятность) принадлежности изучаемой совокупности данных, соответственно будут принимать критериальные значения, подтверждающие несущественность их отклонений от
) и априорно имеющие более высокую степень (вероятность) принадлежности изучаемой совокупности данных, соответственно будут принимать критериальные значения, подтверждающие несущественность их отклонений от  .
. . С целью упрощения расчетов, а в последующем и выводов в анализе многомерной случайной величины часто принимается предположение о нормальности ее распределения.
. С целью упрощения расчетов, а в последующем и выводов в анализе многомерной случайной величины часто принимается предположение о нормальности ее распределения. Вектор
Вектор  сравнивается с постоянным вектором
сравнивается с постоянным вектором  Прямая гипотеза имеет вид
Прямая гипотеза имеет вид  при альтернативной
при альтернативной 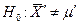
 соответствуют или существенно отличаются от
соответствуют или существенно отличаются от 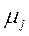
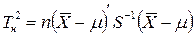
 сопоставляется с критическим, исчисляемым при заранее заданном уровне вероятности а ‑ допустить ошибку в выводах и числе степеней свободы v1 = m и v2 = п - т :
сопоставляется с критическим, исчисляемым при заранее заданном уровне вероятности а ‑ допустить ошибку в выводах и числе степеней свободы v1 = m и v2 = п - т :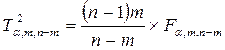
 — табличное значение F-критерия Фишера для известных v1=m и v2=n-m. Многомерная гипотеза подтверждается при
— табличное значение F-критерия Фишера для известных v1=m и v2=n-m. Многомерная гипотеза подтверждается при  и не может быть принята, если
и не может быть принята, если 
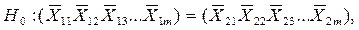
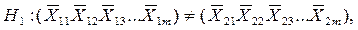
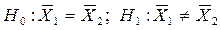
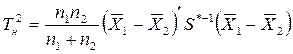
 — векторы средних значений;
— векторы средних значений; – количество объектов в первой и второй выборках;
– количество объектов в первой и второй выборках; ‑ матрица, обратная объединенной ковариационной матрице:
‑ матрица, обратная объединенной ковариационной матрице:  по выборочной совокупности данных, где K ‑ матрица центрированных значений с элементами
по выборочной совокупности данных, где K ‑ матрица центрированных значений с элементами  .
. и с числом степеней свободы
и с числом степеней свободы  :
: .
. нулевая гипотеза
нулевая гипотеза 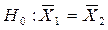 принимается, и вывод о равенстве векторов средних значений следует с вероятностью
принимается, и вывод о равенстве векторов средних значений следует с вероятностью 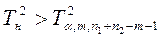 , то гипотеза о равенстве векторов средних значений отвергается.
, то гипотеза о равенстве векторов средних значений отвергается. для сравнений одного или нескольких средних значений из каждой выборочной совокупности осуществляется по формуле:
для сравнений одного или нескольких средних значений из каждой выборочной совокупности осуществляется по формуле: ,
, — вектор, нивелирующий средние значения, не участвующие в сравнении,
— вектор, нивелирующий средние значения, не участвующие в сравнении,  .
. .
. и принимается, когда
и принимается, когда  .
.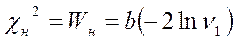 ,
, определяются по формулам:
определяются по формулам: ,
, ,
, ‑ матрица парных корреляций j показателя.
‑ матрица парных корреляций j показателя. — табличными значениями (
— табличными значениями (  ).
).