
|
|
Структура позиционной игры
Лекция 9
Нормализация позиционной игры (продолжение)
Лекция 10
Нормализация позиционной игры (продолжение)
Лекция 11 Позиционные игры с полной информацией
Лекция 12
Биматричные игры
Лекция 13 Смешанные стратеги в биматричных играх
Лекции 14, 15
Лекция 16
Лекция 16
Лекция 18 Игры с природой При решении задач в экономике нередко приходится моделировать ситуации, придавая им игровую схему, в которой один из участников безразличен к результату игры. Такие игры называют играми с природой, или статистическими играми. В статистической игре сознательный игрок А (статистик), заинтересованный в наиболее выгодном для себя исходе, выступает против участника П, безразличного к исходу игры называемого природой. Под природой подразумевается весь комплекс внешних условий, при которых статистику приходится принимать решение. Предположим, что статистик А может использовать m стратегий A1, A2, …,Am. В свою очередь природа может реализовать n состояний П1, П2, …,Пn. Могут быть известны вероятности qj состояний природы Пj ( Таблица 73
При упрощении платёжной матрицы статистической игры следует помнить, что природа может реализовать любое из своих состояний, и поэтому доминируемые столбцы матрицы исключать нельзя. При выборе оптимальной стратегии статистики пользуются обычно различными критериями, основываясь на анализе платёжной матрицы, а также матрицы рисков. Риском rij статистика при использовании им чистой стратегии Аi и состояния природы Пj называется разность между максимальным выигрышем
где Таблица 74
Если вероятности qi состояний Пj природы известны, то можно пользоваться критерием Байеса. В качестве оптимальной, по критерию Байеса, принимается чистая стратегия Аi, при которой максимизируется средний выигрыш статистика, то есть обеспечивается
Если же вероятности состояний природы статистику представляются равновероятными, то по критерию Лапласа, оптимальной считается чистая стратегия Аi, обеспечивающая
Если вероятности qi состояний Пj природы неизвестны, то пользуются критериями Вальда, Сэвиджа и Гурвица. Оптимальной, по критерию Вальда, считается чистая стратегия Аi, при которой наименьший выигрыш
Для смешанных стратегий, по критерию Вальда, оптимальной считается та стратегия, при которой минимальный средний выигрыш статистика будет максимальным, то есть стратегия
По критерию Сэвиджа, оптимальной считается та чистая стратегия Аi, при которой минимизируется величина
Для смешанных стратегий, по критерию Сэвиджа, оптимальной считается та смешанная стратегия, при которой максимальный средний риск статистика
По критерию Гурвица, считается оптимальной чистая стратегия Аi, обеспечивающая
где
Пример 6.7. Банк может приобрести на сумму 18 ден. ед. акции компании K1 начальной стоимостью 6 ден. ед., компании K2 начальной стоимостью 6 ден. ед., компании K3 начальной стоимостью 6 ден. ед. На конец года рынок может оказаться в одном из следующих состояний – П1 и П2. Согласно прогнозам специалистов, дивиденды компании Ki для состояния Пj на конец года составит dij% от номинальной стоимости акции Таблица 75
Требуется: 1. придать описанной ситуации игровую схему, установить характер игры и определить игроков, указав их возможные стратегии; 2. сформировать портфель акций банка, обеспечивающий максимальную прибыль при следующих предположениях: а) известны вероятности q1 = 0.3 и q2 = 0.7 состояний рынка П1 и П2 на конец года ; б) о вероятностях состояний рынка П1 и П2 на конец года ничего определённого сказать нельзя. Решение 1. Используя игровой подход, в качестве игрока А (статистика) примем специалистов банка, принимающих решение о формировании портфеля акций. В качестве второго игрока примем совокупность обстоятельств, обусловливающих то или иное состояние рынка ценных бумаг. Обозначим его через П (природа). Определим возможные стратегии статистика. Пусть банк покупает k1 акций компании K1, k2 акций компании K2 и k3 акций компании K3. Эту стратегию статистика будем обозначать через А(k1, k2, k3). Чтобы вся сумма 18 ден. ед., выделенных банком на приобретение акций, была использована, числа k1, k2, k3 должны удовлетворять условию k1 + k2 + k3 = 18. С учётом этих замечаний возможными чистыми стратегиями игрока А будут В1 = А(3, 0, 0); В2 = А(2, 1, 0); В3 = А(2, 0, 1); В4 = А(1, 2, 0); В5 = А(1, 0, 2); В6 = А(1, 1, 1); В7 = А(0, 3, 0); В8 = А(0, 0, 3); В9 = А(0, 2, 1); В10 = А(0, 1, 2). 2. Задача имеет статистический характер. Вычислим элементы аij платёжной матрицы. Эти коэффициенты выражают суммарную прибыль банка, полученную им в различных ситуациях (Bi, Пi) (
Платёжная матрица игры имеет вид:
Упростим полученную матрицу. Поскольку элементы второй строки не меньше соответствующих элементов третьей, пятой, шестой и десятой строк, то она доминирует над ними. Кроме того, седьмая строка доминирует над девятой. Исключив третью, пятую, шестую, восьмую, девятую и десятую доминируемые строки, придём к следующей платёжной матрице:
Строки этой матрицы соответствуют чистым стратегиям В1 = А(3, 0, 0); В2 = А(2, 1, 0); В4 = А(1, 2, 0); В7 = А(0, 3, 0). Остальные части стратегии игроку А применять невыгодно. Таким образом, можно считать возможными чистыми стратегиями статистика следующие стратегии: А1 = В1 = А(3, 0, 0); А2 = В2 = А(2, 1, 0); А3 = В4 = А(1, 2, 0); А4 = В7 = А(0, 3, 0). Матрица игры будет иметь вид: Таблица 76
3. Найдём нижнюю
Так как А. При известных вероятностях q1 = 0.3 и q2 = 0.7 состояний природы П1 и П2 пользуются критерием Байеса. В качестве оптимальной, по критерию Байеса, принимается чистая стратегия Аi, при которой максимизируется средняя прибыль
Вычисляем среднюю прибыль при использовании каждой из чистых стратегий:
Так как Б. Если оба состояния П1 и П2 представляются статистиком равновероятными, то есть q1 = q2 = 0.5, то можно пользоваться критерием Лапласа, согласно которому оптимальной считается чистая стратегия, обеспечивающая
Находим:
Следовательно, по критерию Лапласа, следует использовать чистые стратегии А3 = А(1,2,0) либо А4 = А(0,3,0). То есть банку рекомендуется приобрести одну акцию компании K1 и две акции компании K2 либо три акции компании K2. Пусть далее о вероятностях состояния рынка ценных бумаг П1 и П2 на конец года ничего не известно. В этом случае можно воспользоваться критериями Вальда, Сэвиджа, Гурвица. В соответствии с критерием Вальда в качестве оптимальной рекомендуется выбрать ту стратегию, которая гарантирует в наихудших условиях максимум выигрыша, т.е. максиминную стратегию:
В нашем случае Согласно критерию Сэвиджа, следует использовать ту стратегию, при которой в наихудших условиях величина риска принимает наименьшее значение:
Построим матрицу рисков
Таблица 77
Следовательно, и по критерию Сэвиджа оптимальной будет чистая стратегия А3. По критерию Гурвица, оптимальной является стратегия, при которой обеспечивается
где Все полученные вычисления представим в таблице (таблица 78). Таблица 78
Следовательно, и по критерию Гурвица оптимальной является чистая стратегия А3 = А(1, 2, 0). Таким образом, наибольшую прибыль банк получит, если его правление приобретёт одну акцию компании K1 и две акции компании K2. Задания для самостоятельной работы Банк может приобрести на сумму b акции компании K1 номинальной стоимостью a1, компании K2 номинальной стоимостью a2, компании K3 номинальной стоимостью a3. На конец года рынок ценных бумаг может оказаться в одном из двух состояний – R1 и R2. Согласно прогнозам специалистов, дивиденды компании Ki для состояния рынка Rj на конец года составят dij% номинальной стоимости ( Требуется: 1. придать описанной ситуации игровую схему, установить характер игры и определить игроков, указав их возможные стратегии; 2. составить платёжную матрицу; 3. сформировать портфель акций банка, обеспечивающий как можно большую прибыль при следующих предположениях: а) известны вероятности q1 и q2 состояний рынка R1 и R2 на конец года; б) о вероятностях состояния рынка R1 и R2 на конец года ничего определённого сказать нельзя. Необходимые числовые данные приведены в таблице. (Варианты 1–14). 1. 2.
3. 4.
5. 6. . 8.
7. 8.
b = 16; γ = 0,7. b = 18; γ = 0,6.
9. 10.
b = 12; γ = 0,6. b = 15; γ = 0,6.
11. 12.
13. 14.
b = 20; γ = 0,6. b = 19; γ= 0,7.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|



























































































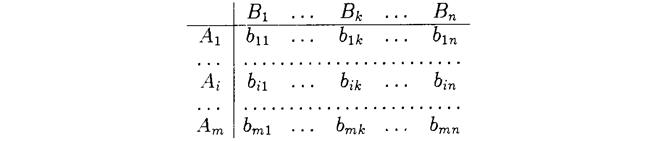































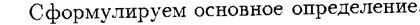
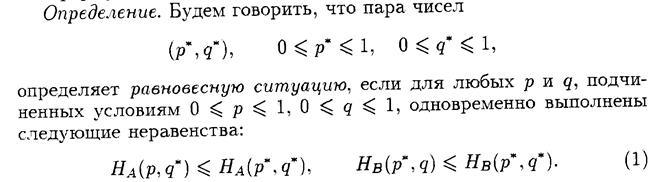


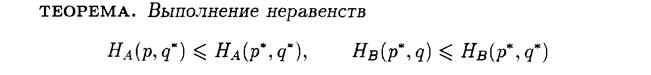


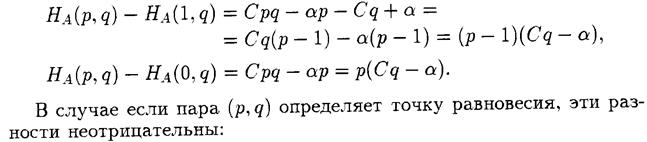









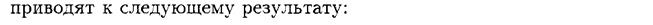




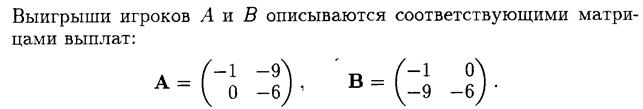































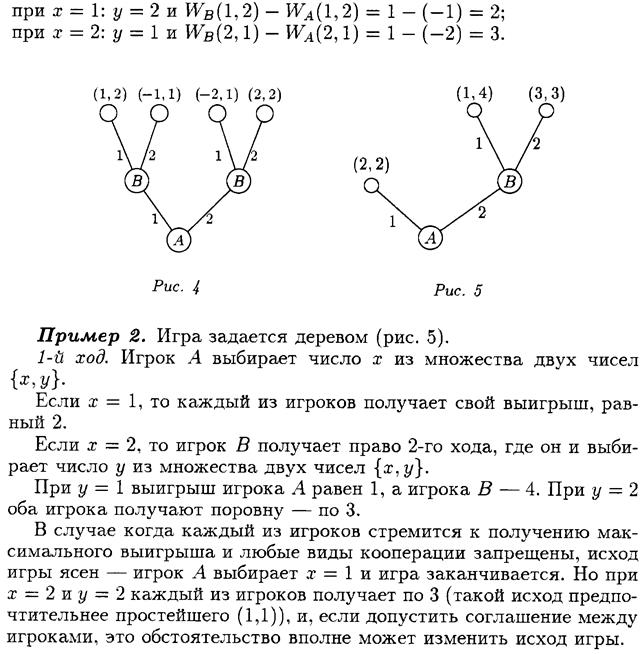















 ). Действуя против природы, статистик может пользоваться как чистыми стратегиями Аi (
). Действуя против природы, статистик может пользоваться как чистыми стратегиями Аi (  ), так и смешанными
), так и смешанными 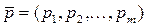 . Если известен численный результат аij для каждой пары стратегий (Аi, Пj), то статистическую игру можно задать платёжной матрицей (таблица 73)
. Если известен численный результат аij для каждой пары стратегий (Аi, Пj), то статистическую игру можно задать платёжной матрицей (таблица 73)
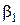
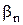
 , который он мог бы получить, зная наверняка, что природой будет реализовано состояние Пj, и тем выигрышем, который он получит, выбрав стратегию Аi. Исходя из этого, элементы матрицы рисков
, который он мог бы получить, зная наверняка, что природой будет реализовано состояние Пj, и тем выигрышем, который он получит, выбрав стратегию Аi. Исходя из этого, элементы матрицы рисков  определяются по формуле
определяются по формуле ,
, – максимально возможный выигрыш статистика при состоянии природы Пj, то есть
– максимально возможный выигрыш статистика при состоянии природы Пj, то есть 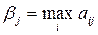 . Очевидно, что все элементы матрицы рисков (таблица 74) неотрицательны.
. Очевидно, что все элементы матрицы рисков (таблица 74) неотрицательны.
 .
. .
. статистика будет максимальным, то есть обеспечивается максимин:
статистика будет максимальным, то есть обеспечивается максимин: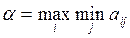 .
. , обеспечивающая
, обеспечивающая .
.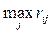 максимального риска, то есть обеспечивающая
максимального риска, то есть обеспечивающая .
.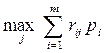 минимизируется, то есть стратегия
минимизируется, то есть стратегия  , обеспечивающая
, обеспечивающая .
.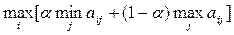 ,
, принадлежит интервалу (0,1) и выбирается из субъективных соображений.
принадлежит интервалу (0,1) и выбирается из субъективных соображений.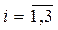 ,
,  (таблица 75)
(таблица 75) ). Например, элемент а11 выражает прибыль банка в ситуации (B1, П1), когда банк приобрёл три акции компании K1 и рынок ценных бумаг на конец года оказался в состоянии П1. Тогда
). Например, элемент а11 выражает прибыль банка в ситуации (B1, П1), когда банк приобрёл три акции компании K1 и рынок ценных бумаг на конец года оказался в состоянии П1. Тогда  . Аналогично находим:
. Аналогично находим: ;
;  ;
; 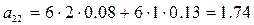 ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
; 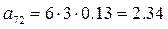 ;
;  ;
; 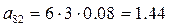 ;
; 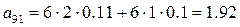 ;
;  ;
;  ;
;  .
. .
. .
.

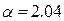
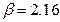
 чистые цены игры:
чистые цены игры: ;
; .
. , то игра не имеет седловой точки.
, то игра не имеет седловой точки. , то есть обеспечивается
, то есть обеспечивается .
.
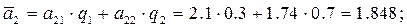

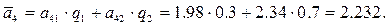
 , то, по критерию Бейеса, оптимальной является чистая стратегия А4 = А(0, 3, 0), то есть правлению банка рекомендуется приобрести три акции компании K2.
, то, по критерию Бейеса, оптимальной является чистая стратегия А4 = А(0, 3, 0), то есть правлению банка рекомендуется приобрести три акции компании K2. .
. ;
;  ;
;  ;
;  .
. .
. .
. , следовательно, по критерию Вальда оптимальной является стратегия А3, то есть рекомендуется приобрести одну акцию компани K1 и две акции компании K2.
, следовательно, по критерию Вальда оптимальной является стратегия А3, то есть рекомендуется приобрести одну акцию компани K1 и две акции компании K2. .
. , где
, где  ,
,  – максимальный возможный выигрыш статистика при состоянии природы Пj (максимальный элемент платёжного столбца, то есть
– максимальный возможный выигрыш статистика при состоянии природы Пj (максимальный элемент платёжного столбца, то есть  )
)

 ,
, . В нашем случае
. В нашем случае  .
.




 ;
; 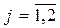 ).
).