
|
|
Сопротивление трения по длине.Потери напора по длине прямой цилиндр трубы опред-тпо ф-ле Дарси-Вейсбаха: hтр=λ В трубах и каналах технических устройств преобладает ткрбулентное движение. Потери напора при турбул-ом движ-ии существенно превышают потери напора при ламинарном движ-ии.
Местные гидравлические сопротивления. Потери напора на местных гидравлических сопротивлениях опред-ся по ф-ле Вейзбаха. Hм – потери напора на мест сопр-ях. Hм=ζ
Установившееся движение ж по трубопроводам. Виды трубопрводов. Трубопровод явл-ся обязат-ым элементом большинства гидросистем и предназначен для транспортирования (перемещения жидкостей). Трубопровод ы изготавливают из ме, пластиков, металл-пластиков, стеклотканей и др материалов. В трубопроводах включается запорная и регулирующая арматура, к-я представляет собой местные гидравлические сопротивления. Арматура: вентили, и др устр-ва. В зависимости от конфигурации различают простые и сложные трубопроводы. 1.Простой трубопровод состоит из труб одинакового диаметра и не имеет ответвлений. 2.Сложный труб-д состоит из простых, соединенных тем или иным способом. К ним относ-ся трубопров-ды с переменным по длине сеч-я. В зависимости от соотношение потерь напора на местных сопротивлениях и потерь напора на прямолин-х участках трубопроводы подраздел-ся на короткие и длинные. Если потери на местных сопротивлениях составляют 10% и более от потерь напора по длине, то такой труб-д наз-т коротким, в противном случае труб-д явл-ся длинным.
Характеристика труб-да. Рассмотрим простой трубопровод произвольно расположенный в пространстве, он состоит из прямых участков одинакового диаметра, между которыми включены местные сопротивления ( поворот, вентиль, фильтр, обратный клапон и т.д. ) рис. d=const, Vср=Q/S=4Q/πd2. Уравнение Бернулли для выделенных сечений: Н1=Н2+h1-2 - разность полных напоров в начальном и конечном сечении трубопровода равна суммарным потерям на трубопроводе. Где Н1 и Н2 – полные напоры в соотствующих сеч-х. h1-2 – суммарные потери напора на трубопроводе. В соответствии с принципом наложения (суперпозиции) суммарные потери напора на простом трубопроводе склад-ся из потерь на прямолинейных участках и потерь на местных сопротивлениях h=h1-2=∑hтр i+∑hм I (1) Подставим соотношение (1) в формулы Дарси – Вейсбаха для потерь на местных сопротивлениях: h=∑λi Зависимость суммарных потерь напора на трубопроводе от расхода жидкости через него h=h(Q)=R(Q)Q2 назыв-ся характеристикой трубопровода, а величина R(Q) – гидравлическим сопротивлениемтрубопровода или просто сопротивление трубопровода. Характеристикой трубопровода, полученная экспериментальным путем выглядит след-им образом: рис. В этом случае говорят о квадратичном законе сопротивления, ему соответствует квадратичная харак-ка трубопровода.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , где l, d – длина и внутр-й диаметр трубы, λ – коэффициент сопротивления трения (коэф-т Дарси). Комплекс λ
, где l, d – длина и внутр-й диаметр трубы, λ – коэффициент сопротивления трения (коэф-т Дарси). Комплекс λ  показывает какую часть от скоростного напора составляет потери напора на преодоление сопротивления по длине. Коэф-т Дарси в общем случае явл-ся функцией от шероховатости внутр-й поверх-ти трубы, ее диаметра, вязкости ж и средней скорости. Λ=λ(Δ,d,υ,Vср)=λ(
показывает какую часть от скоростного напора составляет потери напора на преодоление сопротивления по длине. Коэф-т Дарси в общем случае явл-ся функцией от шероховатости внутр-й поверх-ти трубы, ее диаметра, вязкости ж и средней скорости. Λ=λ(Δ,d,υ,Vср)=λ(  ,Re), Δ – шероховатость, высота неровности,
,Re), Δ – шероховатость, высота неровности, 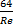 2.При турбулентном режиме коэф-т Дарси опред-ся по ф-ле Альтшуля: λ=0,11(
2.При турбулентном режиме коэф-т Дарси опред-ся по ф-ле Альтшуля: λ=0,11( 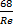 +
+ 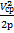 , где Ζ(дзета) безразмерный коэффициент- коэф-т местного сопротив-я. Vср- средняя скорость жидкости в сечении за местным сопротивлением. Коэф-т дзета показывает какую часть от скоростного напора составляют потери напора на местном сопротив-ии. В общем случае дзета зависит от числа Рейнольжса, конфигурации местного сопротив-я и режимов движ-я. 1.При турбул-ом режиме дзета не зависит от числа Рейнолдса, опред-ся толкь формой местного сопротив-я, численне знач-е можно найти в справочниках. 2.При ламинар-ом режиме: ζ=
, где Ζ(дзета) безразмерный коэффициент- коэф-т местного сопротив-я. Vср- средняя скорость жидкости в сечении за местным сопротивлением. Коэф-т дзета показывает какую часть от скоростного напора составляют потери напора на местном сопротив-ии. В общем случае дзета зависит от числа Рейнольжса, конфигурации местного сопротив-я и режимов движ-я. 1.При турбул-ом режиме дзета не зависит от числа Рейнолдса, опред-ся толкь формой местного сопротив-я, численне знач-е можно найти в справочниках. 2.При ламинар-ом режиме: ζ=  +ζкв, где С – постоянная, зависящая от формы местного сопротив-я, ζкв – коэф-ент местного сопротив-я в квадратичной зоне турбулентного режима. Величина С и ζкв можно найти в справочниках.
+ζкв, где С – постоянная, зависящая от формы местного сопротив-я, ζкв – коэф-ент местного сопротив-я в квадратичной зоне турбулентного режима. Величина С и ζкв можно найти в справочниках. = (
= (  ∑li+∑ζi)
∑li+∑ζi)  =(
=(  Q2=R(Q)Q2
Q2=R(Q)Q2