
|
|
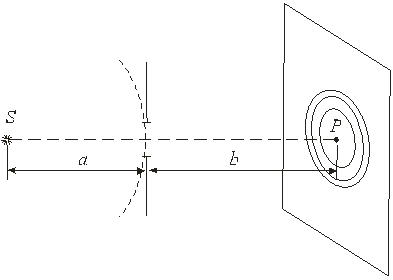
Изучение дифракции Френеля на круглом отверстии и полуплоскостиЛАБОРАТОРНАЯ РАБОТА № 31 Цель работы:освоить методы наблюдения и анализа френелевских дифракционных картин от различных препятствий. Если на пути сферической световой волны поместить небольшой непрозрачный экран с круглым отверстием на расстоянии a от точечного источника S , то на другом сплошном экране, расположенном на расстоянии b от отверстия, будет наблюдаться дифракционная картина в виде чередующихся темных и светлых концентрических колец (рис.1).
Рис.1 Для определения амплитуды (и соответствующей интенсивности) световой волны в точке Р экрана (точка Р находится на прямой, проходящей через источник S и середину отверстия), необходимо сложить амплитуды волн, приходящих от всех открытых зон Френеля, используя метод векторных диаграмм. Радиус m-той зоны Френеля Метод векторных диаграмм позволяет наглядно объяснить распределение интенсивности и при дифракции Френеля на полуплоскости и щели. Остановимся на анализе дифракционной картины от этих преград более подробно.
В этом случае волновой фронт целесообразно разбивать не на кольцевые зоны, как это делалось для круглых препятствий, а на полосатые зоны. Ограничимся случаем, когда волновой фронт плоский. Пусть плоскость волнового фронта АВ перпендикулярна плоскости чертежа (рис.2).
Рис.2 Расстояние от точки наблюдения Р до фронта АВ обозначим через b. Проведем цилиндрические коаксиальные поверхности, ось которых проходит через точку Р перпендикулярно плоскости рисунка, а радиусы увеличиваются на λ/2, т.е. равны b, b+λ/2, b+2λ/2,… Тогда волновой фронт АВ разобьется на прямоугольные полосы, которые называются зонами Шустера. Зоны Шустера отсчитываются вправо и влево от центральной точки О. Таким образом, центральная зона оказывается состоящей из двух зон. Из рис.2 видно:
где rn и хn - расстояния от края n-й зоны до точки Р и точки О, соответственно. Аналогично для зоны с номером n-1 можно записать:
Из этого соотношения следует: Для расчета результирующей амплитуды в точке Р, как и в случае зон Френеля, применим графический метод сложения амплитуд. Каждую зону Шустера разобьем на узкие полоски (подзоны) способом, аналогичным разбиению фронта на зоны Шустера, т.е. внося постоянную разность фаз для волн, идущих от соседних подзон. Колебания, возбуждаемые в точке наблюдения такими подзонами, на векторной диаграмме изобразятся векторами ΔAi , длина которых вначале резко убывает (вследствие значительного отличия площадей первых подзон), а затем становится почти одинаковой. Если перейти к пределу, устремив к нулю ширину каждой подзоны, то вместо ломаной получится плавная кривая, называемая спиралью Корню (рис.3).
Рис.3 Она состоит из двух симметричных ветвей, обвивающихся вокруг фокусов F+ и F-. Верхняя ветвь дает вклад в результирующую амплитуду вторичных волн, идущих от правой половины волнового фронта, а нижняя – от левой. При полностью открытом волновом фронте амплитуда световой волны в т. Р изображается вектором F-F+ . Рассмотрим теперь дифракционную картину на полуплоскости. Обозначим через a0 = ׀F-F+׀ и I0 ~ a02 амплитуду и интенсивность волны при полностью открытом волновом фронте, соответственно. Когда точка Р находится на границе геометрической тени (координата х=0), для нее открыта только правая половина волнового фронта. Колебание в ней представится вектором OF+ = 1/2 F-F+. Ему соответствует амплитуда
Рис.4. При смещении точки Р в область геометрической тени полуплоскость станет закрывать все большее число зон правой половины волнового фронта. Поэтому начало результирующего вектора будет перемещаться по правой ветви, приближаясь к F+. В результате амплитуда и интенсивность колебания в точке Р будет монотонно стремиться к нулю. Если точка Р смещается от границы геометрической тени вправо, в дополнение к правой части волнового фронта будет открываться все возрастающее число зон левой части фронта. При этом начало результирующего вектора амплитуды будет скользить по левой ветви спирали в направлении к F-. В результате амплитуда проходит через ряд максимумов (первый из них равен длине отрезка NF+) и минимумов (первый соответствует длине отрезка LF+) (рис.3). Зависимость интенсивности света I от расстояния x, показана на рис.4. Задание 1. Определение длины волны излучения лазерного источника по дифракционной картине. Принадлежности: лазер, короткофокусная линза Л1, пластина с круглыми отверстиями О, линза Л2, экран Э. Соберите установку на оптической скамье для наблюдения дифракции на круглом отверстии и отъюстируйте ее. Для этого: 1. На одном конце оптической скамьи установите лазер, а на другом - экран Э. Включите лазер и добейтесь, чтобы луч распространялся вдоль оптической скамьи. Отметьте крестиком на листе бумаги, укрепленном на экране, точку падения лазерного луча. 2. Установите перед лазером короткофокусную линзу Л1 (f = 1см) так, чтобы центр светлого пятна на экране совпадал с крестиком. 3. Перед линзой (на расстоянии 10 – 15 см от линзы) поместите пластинку с круглыми отверстиями, предварительно измерив диаметр 3-го и 4-го отверстий с помощью компаратора. Введя в луч одно из указанных отверстий, добейтесь появления дифракционной картины на экране вблизи крестика. После чего закрепите пластинку в рейтере. 4. Перемещая пластинку с отверстиями вдоль оптической скамьи, оставляя неизменным расстояние от линзы до экрана (~ 85см), добейтесь появления в центре картины темного пятна. Для облегчения наблюдения дифракционной картины на экране воспользуйтесь линзой Л2, как лупой. Измерьте расстояния a1 и b1 (см. рис.1, a1 следует отсчитывать от заднего фокуса линзы Л1 до экрана с отверстиями). 5. Продолжайте перемещать отверстие, наблюдая за изменением освещенности в центре экрана, до появления следующего темного пятна (в этом случае число зон Френеля, открываемых отверстием, изменяется на Δm = 2). Измерьте a2 и b2. 6. По формуле 7. Повторите эксперимент для другого отверстия. Задание 2. Наблюдение дифракционной картины на полуплоскости. Принадлежности: лазер, короткофокусная линза Л1, пластина – полуплоскость ППл, экран Э.
1. Для наблюдения дифракции на полуплоскости, соберите установку, оптическая схема которой подобна той, которая использовалась в задании 1, заменив диафрагму с отверстиями на полуплоскость (ППл). Зарисуйте полученную дифракционную картину и объясните ее. Контрольные вопросы 1. Явление дифракции света. 2. Принцип Гюйгенса–Френеля. 3. Классификация дифракционных явлений. Дифракция Френеля и Фраунгофера. 4. Дифракция Френеля на круглом отверстии. Зоны Френеля. Метод векторных диаграмм. 5. Дифракция Френеля на щели и полуплоскости. Зоны Шустера. Спираль Корню. 6. Сформулируйте цель работы, опишите экспериментальную часть и обсудите результаты.
ЛАБОРАТОРНАЯ Работа №32 АМПЛИТУДНАЯ И ФАЗОВАЯ ЗОННЫЕ ПЛАСТИНКИ Цель работы: изучение амплитудной и фазовой пластинок. Рассмотрим дифракцию на круглом отверстии сферической световой волны, испущенной точечным источником S. Интенсивность света в точке наблюдения Р будет существенно зависеть от числа зон Френеля, которое открывает отверстие. Радиус m-ой зоны Френеля rm находится по формуле:
где a и b – расстояния от центра отверстия до источника света S и точки P, соответственно, l - длина волны. Колебания от соседних зон Френеля приходят в точку Р в противофазе и ослабляют друг друга. Если закрыть все четные (или нечетные) зоны Френеля, то световые колебания от открытых зон будут приходить в одной фазе, и в точке P будет наблюдаться яркая освещенная точка, представляющая собой изображение источника S. На практике это достигается с использованием зонных пластинок.
Для того, чтобы избежать потерь на поглощение и увеличить эффективность сбора световой энергии в точке Р, используют фазовую зонную пластинку. Она изменяет фазу колебаний от всех четных зон на p. При этом амплитуда результирующего колебания по сравнению с амплитудной зонной пластинкой увеличивается в точке Р в два раза, а интенсивность, соответственно, в четыре.
Сечение такой пластинки и соответствующая векторная диаграмма показаны на рис.2. Для видимого света величина h приблизительно равна 0,5 мкм. Поскольку оптический путь световой волны зависит от геометрического пути и показателя преломления среды, то фазовую зонную пластинку можно изготовить либо путем изменения рельефа поверхности, либо путем изменения показателя преломления материала подложки. Рельеф может быть нарезан с помощью алмазного резца, что делает этот метод изготовления более доступным для применения, однако он имеет существенный недостаток из-за недостаточной точности нарезки и ограниченности изготовления неосесимметричных элементов. Изменение коэффициента преломления можно достичь, используя процессы диффузии, химические и физические структурные изменения материалов под действием излучения или путем имплантации атомов и ионов. Несмотря на высокую точность изготовления, получаемые таким образом изделия имеют малую механическую прочность. Другим недостатком этого способа является невозможность тиражирования фазовых пластинок. Зонная пластинка, подобно линзе, обладает фокусирующим действием. Формулу (1) можно переписать в виде формулы тонкой линзы:
где параметр f равен:
Расстояние f называется фокусным расстоянием зонной пластинки.
Рис. 3 Оптическая схема установки
Фокусирующее действие зонной пластинки будет наблюдаться и в случае, когда в одной кольцевой зоне будет укладываться по 3, 5, … и.т.д. зон Френеля. Следовательно, в отличие от линзы, для каждой длины волны зонная пластинка имеет несколько фокусов. Это обстоятельство аналогично наличию максимумов различных порядков у дифракционных решеток. В настоящей работе используется амплитудная зонная пластинка, представляющая собой уменьшенную фотографию чертежа зонной пластинки. На рис. 3 приведена фотография экспериментальной установки. Непрозрачный экран D с крестообразным вырезом освещается с помощью собирающей линзы - конденсора О1 ртутной лампой Л. Лучи, прошедшие через крестообразный вырез, попадают на зонную пластинку П. Зонная пластинка создает изображение креста в некоторой плоскости, которое рассматривается с помощью микроскопа О2.
Рис. 4 Измерительный микроскоп МИР 12.
ХОД работы Задание 1. Определение радиусов колец зонной пластинки
Измерьте внешние радиусы первых пяти - шести темных или светлых колец зонной пластинки, нумеруя их нечетными или четными номерами, соответственно. Для измерения используется измерительный микроскоп МИР-12 (Рис. 4). Подготовка микроскопа к измерениям выполняется следующим образом: зонную пластинку с такими же параметрами, как в установке, кладут на предметный столик 1 и освещают светом, отраженным от зеркала 2. Наблюдая в окуляр 3, передвигают рукой окуляр в вертикальном направлении до тех пор, пока изображение зонной пластинки не будет достаточно резким. Точная фокусировка достигается вращением объектива 4 за нижнее накатное кольцо. Верхнее накатное кольцо служит для закрепления объектива. Установка окуляра на резкость нитей выполняется путем вращением оправы глазной линзы 3. Далее приступайте к измерениям. Поскольку визирные линии окуляра не проходят через центр поля зрения, зонную пластинку следует несколько сместить по отношению к центру поля зрения для удобства измерений. Отсчет снимайте по шкале 5 с ценной деления 1 мм и барабану 6 с ценной деления 0,01 мм. При измерениях необходимо учесть наличие «мертвого хода» у микрометрического винта. Чтобы избежать связанной с «мертвым ходом» погрешности, микрометрический винт следует вращать в одну сторону, последовательно снимая отсчеты. Вследствие того, что определить центр пластинки трудно, целесообразно проводить измерения диаметров колец, а не их радиусов. Диаметр кольца находится как разность двух отсчетов, сделанных при совпадении визирной линии с внешним контуром кольца в диаметрально противоположных точках. Задание 2. Определение фокусного расстояния зонной пластинки Фокусное расстояние зонной пластинки может быть определенно двумя способами. Первый способ. Фокусное расстояние можно найти по формуле (3) если известны радиусы зон. Зная радиусы пяти-шести зон из первого упражнения и длину волны света ртутной лампы l=578 нм, вычислите, используя (3), фокусное расстояние зонной пластинки. Сравните насколько точно совпадают значения фокусного расстояния, полученные для различных зон. Результат представите как среднее арифметическое из пяти-шести значений. Второй способ. Фокусное расстояние можно найти по формуле (2), измеряя расстояния a и b. Для этого включите ртутную лампу, перемещением зонной пластинки и окуляра микроскопа добейтесь, чтобы в поле зрения окуляра было отчетливо видно яркое резкое изображение желтого креста в увеличенном масштабе. Измерите с помощью линейки расстояние а от диафрагмы до зонной пластинки и расстояние b от зонной пластинки до фокальной плоскости окуляра. Положение каждого из этих элементов отмечено указателями на рейтерах. Вычислите фокусное расстояние по формуле (2). Сравнить результаты измерений фокусного расстояния этими двумя способами. Задание 3. Определение длины волны зеленной и фиолетовой линии спектра ртути. С помощью зонной пластинки можно определить длину световой волны, воспользовавшись следующим соотношением:
Значения Задание 4. Изучение фазовой зонной пластинки. Снимите с рейтера амплитудную зонную пластинку и установите фазовую зонную пластинку. На расстоянии в несколько десятков сантиметров от пластинки установите лист белой бумаги, который будет служить экраном. Небольшим перемещением пластинки или экрана добейтесь появления хорошего изображения креста на экране. Отъюстируйте пластинку в фокальной плоскости с помощью зажимного винта на ее оправе. Для этого небольшими поворотами пластинки вокруг вертикальной оси и небольшими сдвигами в направлении, перпендикулярном оси, добейтесь наилучшего качества изображения креста. Путем перемещения фазовой зонной пластинки вдоль оптической оси пронаблюдайте несколько цветных изображений креста. КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Принцип Гюйгенса–Френеля. Интерференция вторичных волн. 2. Метод зон Френеля. 3. Дифракция Френеля на круглом отверстии. 4. Метод векторных диаграмм. 5. Амплитудная зонная пластинка. 6. Фазовая зонная пластинка. 7. Зонная пластинка как спектральный прибор.
Литература: 1. И.Е.Иродов. Задачи по общей физике, изд.5, исп., М., ЛБЗ, 2003 2. Д.В. Сивухин. Курс общей физики. Том 4. Оптика. изд. 3, М., Физматлит., 2006. 3. Г.С. Ландсберг. Оптика, изд. 6, М., Физматлит, 2006. 4. И.В. Савельев. Курс общей физики. Книга 4. Волны. Оптика, М., АСТ, 2006 5. А.И. Фишман. Фазовые оптические элементы – киноформы. Соровский образовательный журнал. № 12, С. 76-83, 1999. 6. А.А. Городецкий, А.И. Фишман Синтезированные голографические элементы – киноформы - в курсе общей физики. Журнал Моск. физ. о-ва. Сер. Б, Физическое образование в вузах. Т.1, № 2, С. 71-84, 1995. ЛАБОРАТОРНАЯ Работа №33 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Если радиус отверстия r0 окажется равным радиусу m-й зоны Френеля rm, то можно определить число зон Френеля m, открываемых данным отверстием:
Если радиус отверстия r0 окажется равным радиусу m-й зоны Френеля rm, то можно определить число зон Френеля m, открываемых данным отверстием:  . Видно, что число открытых зон Френеля зависит не только от r0, но и от расстояний а и b. Меняя эти расстояния, можно изменять число зон, открываемых отверстием r0. Если окажется, что Δm = 1, то в центре дифракционной картины светлое пятно сменится на темное или наоборот, темное - на светлое.
. Видно, что число открытых зон Френеля зависит не только от r0, но и от расстояний а и b. Меняя эти расстояния, можно изменять число зон, открываемых отверстием r0. Если окажется, что Δm = 1, то в центре дифракционной картины светлое пятно сменится на темное или наоборот, темное - на светлое.
 , (1)
, (1) . Тогда
. Тогда (2)
(2) . Отсюда легко могут быть найдены все
. Отсюда легко могут быть найдены все  . Т.к.
. Т.к. 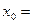 0, то
0, то  ,
,  , …,
, …,  . Ширины зон Шустера Δхn будут равны:
. Ширины зон Шустера Δхn будут равны: 
 ,
,  ...
...  . Они монотонно убывают Δх1 : Δх2 : Δх3 : Δх4 ... = 1 : 0,41 : 0,32 : 0,27: … .
. Они монотонно убывают Δх1 : Δх2 : Δх3 : Δх4 ... = 1 : 0,41 : 0,32 : 0,27: … .
 и интенсивность I0/4 (рис 4).
и интенсивность I0/4 (рис 4).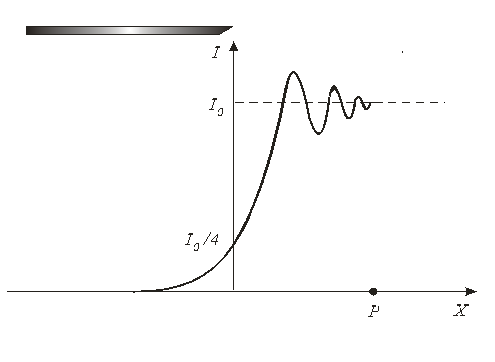
 определите длину волны лазера и оцените погрешность измерений.
определите длину волны лазера и оцените погрешность измерений. , (1)
, (1)
 Для того чтобы перекрыть, например, все четные зоны Френеля необходимо поставить на пути световой волны амплитудную зонную пластинку, которая представляет собой круглый дифракционный экран, четные зоны Френеля которого непрозрачны, а нечетные – прозрачны. При прохождении света через амплитудную зонную пластинку половина световой энергии падающей волны теряется из-за поглощения в непрозрачных областях пластинки (рис. 1).
Для того чтобы перекрыть, например, все четные зоны Френеля необходимо поставить на пути световой волны амплитудную зонную пластинку, которая представляет собой круглый дифракционный экран, четные зоны Френеля которого непрозрачны, а нечетные – прозрачны. При прохождении света через амплитудную зонную пластинку половина световой энергии падающей волны теряется из-за поглощения в непрозрачных областях пластинки (рис. 1). Чтобы изменить фазу волны на p, следует изменить ее оптический путь на l/2. Для этого толщину стеклянной пластинки в местах, соответствующих четным зонам Френеля, нужно уменьшить или увеличить на величину h, равную (см. например, задачу 4.117 в [1]):
Чтобы изменить фазу волны на p, следует изменить ее оптический путь на l/2. Для этого толщину стеклянной пластинки в местах, соответствующих четным зонам Френеля, нужно уменьшить или увеличить на величину h, равную (см. например, задачу 4.117 в [1]):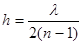

 , (2)
, (2)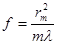 . (3)
. (3) Как видно из (3), характерной особенностью зонной пластинки по сравнению с линзой являет то, что ее фокусное расстояние зависит от длины волны. Это явление называют хроматизмом.
Как видно из (3), характерной особенностью зонной пластинки по сравнению с линзой являет то, что ее фокусное расстояние зависит от длины волны. Это явление называют хроматизмом.
 .
. возьмите из упражнения 1. Фокусное расстояние зонной пластинки определите вторым способом. Для этого перемещением окуляра получите в поле зрения окуляра яркое, резкое, увеличенное изображение зеленого креста и измерите расстояния a и b. Затем те же измерения проделайте с фиолетовой линией. Найдите фокусные расстояния для зеленой и фиолетовой линий и вычислите длины волн этих линий.
возьмите из упражнения 1. Фокусное расстояние зонной пластинки определите вторым способом. Для этого перемещением окуляра получите в поле зрения окуляра яркое, резкое, увеличенное изображение зеленого креста и измерите расстояния a и b. Затем те же измерения проделайте с фиолетовой линией. Найдите фокусные расстояния для зеленой и фиолетовой линий и вычислите длины волн этих линий.