|
|
Раздел Дифференциальное исчислениеМатематика Методические указания по изучению дисциплины для обучающихся на заочном отделении по специальности 38.02.03 Операционная деятельностьв логистике Методические рекомендации составлены в соответствии с Федеральным государственным образовательным стандартом среднего профессионального образования и в соответствии с рабочей программой по ЕН.01 Математика по специальности 19.02.10 Технология продукции общественного питания утвержденного приказом Министерства образования и науки Российской Федерации от 29 октября 2013 г. № 1199
Организация-разработчик: ГАПОУ ТО «Тюменский техникум индустрии и питания, коммерции сервиса»
Разработчики: Л.У. Хайруллина. преподаватель математики
Методические рекомендации рассмотрены на заседании цикловой комиссии естественнонаучных и математических дисциплин Протокол № 1 «28» августа 2015 г. Председатель цикловой комиссии: __________ Ю.Я. Кадырова (Подпись)
Пояснительная записка
Методические рекомендации по дисциплине ЕН.01 Математика создан в помощь подготовки к текущему и итоговому контролю по дисциплине. Методические рекомендации включает теоретический блок, перечень практических занятий, задания по самостоятельному изучению тем дисциплины, вопросы для самоконтроля, перечень точек рубежного контроля, а также вопросы и задания по промежуточной аттестации (при наличии экзамена). Приступая к изучению новой учебной дисциплины, Вы должны внимательно изучить список рекомендованной основной и вспомогательной литературы. Из всего массива рекомендованной литературы следует опираться на литературу, указанную как основную. По каждой теме перечислены основные понятия и термины, вопросы, необходимые для изучения (план изучения темы), а также краткая информация по каждому вопросу из подлежащих изучению. Наличие тезисной информации по теме позволит Вам вспомнить ключевые моменты, рассмотренные преподавателем на занятии. Основные понятия курса приведены в глоссарии. После изучения теоретического блока приведен перечень практических работ, выполнение которых обязательно. Наличие положительной оценки по практическим работам необходимо для получения зачета по дисциплине и/или допуска к экзамену По итогам изучения дисциплины проводится зачет. В результате освоения дисциплины Вы должны уметь: - решать прикладные задачи в области профессиональной деятельности. В результате освоения дисциплины Вы должны знать: - значение математики в профессиональной деятельности и при освоении основной профессиональной образовательной программы; - основные математические методы решения прикладных задач в области профессиональной деятельности; - основы интегрального и дифференциального исчисления. В результате освоения дисциплины у Вас должны формироваться общие компетенции (ОК): ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес. ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество. ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность. ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития. ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности.
ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями. ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий. ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации. ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности. профессиональные компетенции (ПК): 1. Организация процесса приготовления и приготовление полуфабрикатов для сложной кулинарной продукции. ПК 1.1. Организовывать подготовку мяса и приготовление полуфабрикатов для сложной кулинарной продукции. ПК 1.2. Организовывать подготовку рыбы и приготовление полуфабрикатов для сложной кулинарной продукции. ПК 1.3. Организовывать подготовку домашней птицы для приготовления сложной кулинарной продукции. 2. Организация процесса приготовления и приготовление сложной холодной кулинарной продукции. ПК 2.1. Организовывать и проводить приготовление канапе, легких и сложных холодных закусок. ПК 2.2. Организовывать и проводить приготовление сложных холодных блюд из рыбы, мяса и сельскохозяйственной (домашней) птицы. ПК 2.3. Организовывать и проводить приготовление сложных холодных соусов. 3. Организация процесса приготовления и приготовление сложной горячей кулинарной продукции. ПК 3.1. Организовывать и проводить приготовление сложных супов. ПК 3.2. Организовывать и проводить приготовление сложных горячих соусов. ПК 3.3. Организовывать и проводить приготовление сложных блюд из овощей, грибов и сыра. ПК 3.4. Организовывать и проводить приготовление сложных блюд из рыбы, мяса и сельскохозяйственной (домашней) птицы. 4. Организация процесса приготовления и приготовление сложных хлебобулочных, мучных кондитерских изделий. ПК 4.1. Организовывать и проводить приготовление сдобных хлебобулочных изделий и праздничного хлеба. ПК 4.2. Организовывать и проводить приготовление сложных мучных кондитерских изделий и праздничных тортов. ПК 4.3. Организовывать и проводить приготовление мелкоштучных кондитерских изделий. ПК 4.4. Организовывать и проводить приготовление сложных отделочных полуфабрикатов, использовать их в оформлении. 5. Организация процесса приготовления и приготовление сложных холодных и горячих десертов. ПК 5.1. Организовывать и проводить приготовление сложных холодных десертов. ПК 5.2. Организовывать и проводить приготовление сложных горячих десертов. 6. Организация работы структурного подразделения. ПК 6.1. Участвовать в планировании основных показателей производства. ПК 6.2. Планировать выполнение работ исполнителя. ПК 6.3. Организовывать работу трудового коллектива. ПК 6.4. Контролировать ход и оценивать результаты выполнения работ исполнителя. ПК 6.5. Вести утвержденную учетно-отчетную документацию.
СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
Раздел Дифференциальное исчисление Тема Производная функции, физический и геометрический смысл. Производная сложной функции. Основные понятия и термины по теме: производная функции, геометрический смысл производной, физический смысл производной, правила дифференцирования, производная сложной функции. Краткое изложение теоретических вопросов: Производной функции Производную функции
Геометрический смысл производной. Производная функции Физический смысл производной. Если Функция, имеющая производную в данной точке, называется дифференцируемой в этой точке. Операция нахождения производной называется дифференцированием. Геометрический симысл производной Производная функции Основные правила дифференцирования Теорема: Производная суммы (разности) двух дифференцируемых функции равна сумме (разности) производных этих функций:
Теорема: Производная произведения двух дифференцируемых функций равна произведению первой функции на производную второй плюс произведению второй функции на производную первой, т.е.:
Следствие: Постоянный множитель можно выносить за знак производной: Теорема: Производная частного двух дифференцируемых функций определяется формулой:
Производной второго порядка (второй производной), функции
Производная сложной функции: Теорема: Если
Пример: Найти производную функции Считая
Пример: Найти производную функции Применяя формулы находим Пример: Найти производную функции Так как Пример: Найти производную функции Применяя таблицу производных Вопросы для самоконтроля по теме: 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|

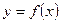 в точке
в точке 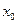 называется предел отношения приращения этой функции к приращению аргумента, при условии, что приращение аргумента стремится к нулю.
называется предел отношения приращения этой функции к приращению аргумента, при условии, что приращение аргумента стремится к нулю. или
или  . Следовательно, по определению
. Следовательно, по определению или
или 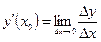
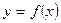 при
при  равна угловому коэффициенту касательной к графику данной функции в точке
равна угловому коэффициенту касательной к графику данной функции в точке  , т.е.
, т.е. 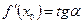 , где
, где 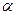 - угол наклона касательной к оси
- угол наклона касательной к оси  прямоугольной декартовой системы координат.
прямоугольной декартовой системы координат.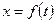 - законпрямолинейного движения точки, то
- законпрямолинейного движения точки, то  - скорость этого движения в момент времени
- скорость этого движения в момент времени  .
. .
.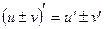
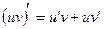
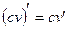
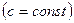

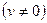
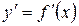 и обозначается:
и обозначается: ,
,  .
. и
и  - дифференцируемые функции своих аргументов, то производная сложной функции
- дифференцируемые функции своих аргументов, то производная сложной функции  существует и равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, т.е.:
существует и равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, т.е.: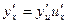
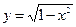 .
. и применяя формулу получаем
и применяя формулу получаем  ,
,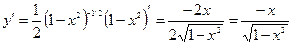
 .
.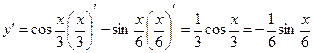
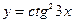 .
. , где
, где  ,
,  , то формулу применяем дважды на основании формул получаем
, то формулу применяем дважды на основании формул получаем