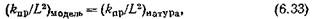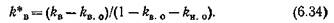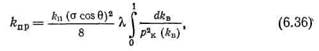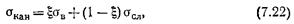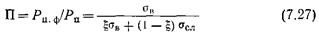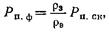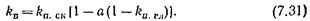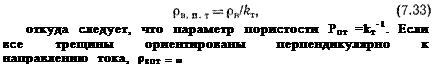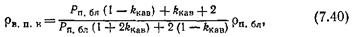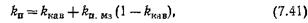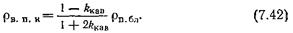МЕТОДЫ ОПРЕДЕЛЕНИЯ ОТНОСИТЕЛЬНЫХ ФАЗОВЫХ ПРОНИЦАЕМОСТЕЙ(ОФП)

Существуют прямые и косвенные методы определения ОФП. К прямым относятся лабораторные методы: 1) стационарной (установившейся) фильтрации и 2) вытеснения. К косвенным: расчетные методы по кривым капиллярного давления; по про­мысловым данным; по данным геофизических исследований .скважин. Для соблюдения геометрического подобия лабораторного моделирования Д. А. Эфрос рекомендует соблюдать, соотноше­ние:

где L — длина.

В экспериментах по стационарной фильтрации условие (6.33) может быть соблюдено применительно к элементу пласта (трубке тока), где существуют те же условия фильтрации, что и в лаборатории.

В лабораторных опытах по методу вытеснения приближен­ное подобие соблюдается экспериментальным подбором скоро­сти вытеснения так, чтобы сделать выполнимым условие (6.33). Выбранная скорость вытеснения будет зависеть от осо­бенностей изучаемого объекта.

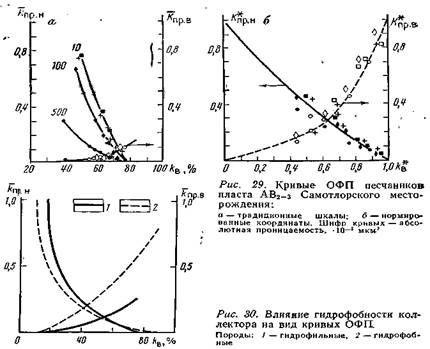
На основании изучения образцов керна получают значения ОПФ, отображающие свойства конкретной породы. На рис. 29, а изображены усредненные кривые ОФП, полученные методом установившейся двухфазной фильтрации на коллекции образцов полимиктового песчаника АВ_2-3 Самотлорского нефтяного мес­торождения.

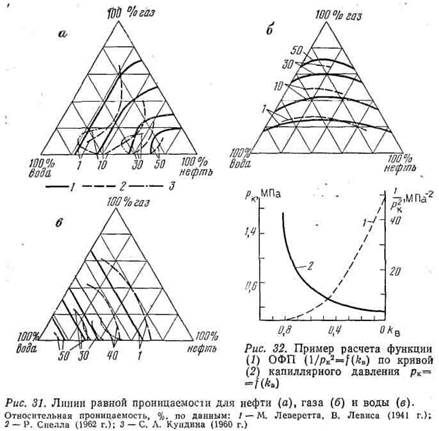
В силу специфического строения порового пространства кри­вые ОФП для нефти в этих породах разделились по абсолютной проницаемости. Зависимости ОФП для воды характеризуются одной кривой. Для того чтобы убедиться, что все кривые ОФП для нефти принадлежат одному литотипу, перестраивают кри­вые в нормированных координатах по способу, предложенному Р. Коллинзом. Нормированные значения водонасыщенности определяют:

где k_пр.нво и k_пр.вно — относительные проницаемости для нефти и воды соответственно при остаточных водо- и нефтенасыщении.

Кривые ОФП для нефти в нормированных координатах (см. рис. 29, б) описываются единой кривой. Сохранилась единой за­висимость ОФП для воды, что является признаком единого ли-тотипа изученной породы, имеющей одинаковую структуру пе­рового пространства. Последнее обстоятельство позволяет ис­пользовать лабораторные зависимости в нормированных коор­динатах для расчета ОФП образцов с различной абсолютной проницаемостью, но обладающих подобной структурой порового пространства.

На характер экспериментальных кривых ОФП помимо струк­туры порового пространства оказывают влияние также ряд дру­гих факторов: поверхностное и межфазное натяжения; гидро-фобность коллектора, температура; скорость фильтрации; изме­нение направления насыщения и др.

При снижении межфазного натяжения σфазовые проницае­мости незначительно возрастают и кривые ОФП поднимаются. Проницаемость для нефти существенно возрастает лишь при очень низких значениях о (менее 10^-3 Н/м). Увеличение σсу­жает диапазон совместного течения флюидов (Д. О. Амаефул, Л. Л. Хэнди, 1982 г.).

Гидрофобизация коллекторов в природных условиях обу­словлена адсорбцией на поверхности породы полярных компо­нентов нефти и битумоидов. С увеличением гидрофобности по­верхности пересечение кривых ОФП смещается влево, в сторо­ну более низких водонасыщений (рис. 30). В соответствии с этим относительная проницаемость для воды существенно воз­растает, а для нефти — снижается. Кроме того, отношение отно­сительной проницаемости для нефти при остаточном водонасы­щений (k_пр.нво) к относительной проницаемости для воды при остаточном нефтенасыщении (k_пр.вно), равно 0,3 в гидрофиль­ных коллекторах и близко к I в гидрофобных (С. Г. Раза, Л. Е. Трейбер, Д. Л. Арчер).

С увеличением температуры уменьшается поверхностное на­тяжение, изменяется межфазное натяжение, увеличивается гидрофильность. породы. С увеличением температуры ОФП для нефти растет, а для воды изменяется в ту или другую сторону (кривые ОФП смещаются в сторону повышенных водонасыще­ний, особенно при низком межфазном натяжении), ОФП для газа практически не изменяются от температуры.

Значения ОФП с увеличением скорости фильтрации возрас­тают. И хотя физическая сторона этого явления не совсем ясна, опыты по определению ОФП рекомендуется проводить на ско­ростях фильтрации, близких к пластовым условиям конкретно­го месторождения.

Cо скоростью фильтрации связано возникновение так назы­ваемых концевых эффектов — повышение насыщенности кернов смачивающей фазой (водой) на выходном конце, а также на стыках составного образца. С увеличением скорости фильтра­ции концевой эффект снижается (Т. Т. Ричардсон и др.). Эти обстоятельства требуют использования длинных образцов (в ко­торых концевые образцы играют роль насадок, а измерение производится в центре) и тщательной пришлифовки образцов.

Процесс вытеснения несмачивающей фазы (нефти) смачи­вающей (водой) называют впитыванием жидкости, обратный процесс — вытеснение воды нефтью — дренированием. При по­следовательном проведении этих двух процессов на кривых ОФП наблюдается гистерезис, объясняющийся неадекватным распределением нефти в порах при течении этих процессов. Особенно заметен гистерезис кривых ОФП для несмачивающей фазы (нефти).

Трехфазная фильтрация (нефть, газ и вода) может иметь место при разработке месторождений нефти на поздней стадии, газовых месторождений с нефтяной оторочкой, при закачке га­за или водогазовых смесей в нефтяной пласт.

Результаты экспериментальных исследований трехфазной фильтрации весьма немногочисленны (М. К- Леверетт, В. Б. Левис, 1941 г.; Б. Н. Коудел и др., 1951 г; С. А. Кундин, 1960 г.; С. Н. Пирсон и др., 1964 г.; В. А. Иванов, 1965 г.).

Результаты измерений относительных проницаемоетей при трехфазной фильтрации принято изображать в виде треуголь­ных диаграмм (рис. 31) или задавать в виде таблиц.

Результаты большинства из указанных выше авторов каче­ственно согласуются с первыми данными М. К- Леверетта на насыпном грунте, которые сформулированы следующим обра­зом:

проницаемость для воды зависит только от водонасыщенности;

проницаемость для нефти и газа зависит от насыщенности всех трех фаз;

проницаемость для газа в трехфазной системе несколько ни­же, чем при той же газонасыщенности в двухфазной системе;

проницаемость для нефти в трехфазной системе может быть больше или меньше ее проницаемости в двухфазной системе при тех же коэффициентах нефтенасыщения;

фазовые проницаемости для нефти, газа и воды не зависят от вязкости нефтяной фазы;

существует сравнительно небольшая область, в которой про­исходит фильтрация всех трех фаз.

В количественном отношении результаты разных авторов существенно отличаются. Очень много еще неясного в механиз­ме трехфазной фильтрации.

Таким образом, для повышения достоверности лаборатор­ных определений ОФП исследования необходимо проводить с соблюдением всех критериев подобия натурных и лаборатор­ных условий. С этой целью должны использоваться естествен­ные керны пород, натуральная нефть и модель пластовой воды, природные давление и температура.

В расчетных методах используется уравнение У. Пурсела, устанавливающее связь между проницаемостью k_пр пористо­стью k_п и кривой капиллярного давления p_K = f(k_B):

где σ — поверхностное натяжение; θ — угол смачиваемости; λ —- литологический коэффициент, определенный Н. Бурдайном как относительная извилистость поровых каналов.

Методика расчета ОФП по кривым капиллярного давления сводится к следующему. Экспериментально определенные кри­вые капиллярного давления p_K=f(k_B) перестраиваются графи­чески в функцию 1/p²_K = f(k_B) (рис. 32).

Для выбранных значений k_B рассчитывают значения интег­ралов в формулах (6.37). Значения искомых интегралов соот­ветствуют площади под кривой 1/р²_к=/(k_в) для заданных пре­делов интегрирования. Затем, задаваясь величинами k_в.ои k_н.о, определяют ОФП.

Капиллярные кривые можно использовать для вычисления ОФП по более сложным трехмерным сеточным моделям (Фэтт, Ентов и Чен-Син, Саффман, Николаевский). Однако в этом случае требуются вычислительные программы.

В методах определения ОФП по промысловым и геофизи­ческим данным много неоднозначности и они не получили ши­рокого распространения.

ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА

Проводимость среды — способность пропускать электричес­кий ток, сопротивление — способность препятствовать прохож­дению тока. Удельная электрическая проводи­мость среды σ и ее удельное электрическое со­противление ρ¹ равны соответственно проводимости Σ и сопротивлению R единицы объема (1 м³) среды. Размерность σ и ρ соответственно Сим/м и Ом∙м.

Проводимость среды обусловлена переносом электрических зарядов сквозным током — электронов, ионов, дырок. В веще­ствах с электронной проводимостью (металлы, графит) ток рас­пространяется благодаря движению электронов. В диэлектри­ках природа проводимости ионная, в полупроводниках — дыроч­ная. Растворы электролитов обладают ионной проводимостью.

В высокочастотном поле в средах с низкой проводимостью, представленных диэлектриками и полупроводниками, наряду со сквозным током j_скв появляется релаксационная составляющая тока j_рел, обусловленная поляризацией частиц среды. В резуль­тате поляризации наряду с основным полем возникает допол­нительное, направленное противоположно основному, поляризу­ющему. Поляризация Р пропорциональна поляризующему по­лю: Р = άЕ, где ά —поляризуемость среды. Поляризуемость ха­рактерна, как правило, для сред с низкой проводимостью — ди­электриков. Любое вещество способно быть проводником и по­ляризоваться; в общем случае его относительная диэлектричес­кая проницаемость определяется как ε=1+4πά. Различают по­ляризации смещения, ориентационную, структурную.

1. Поляризация смещения состоит в упругом сме­щении зарядов под действием внешнего поля. К этой группе относят электронную, ионную и атомную поляризацию.

Электронная поляризация заключается в смеще­нии электронов атома относительно его ядра, характеризует­ся временем т смещения и релаксации порядка 10^-15 с, не за­висит от частоты поля со вплоть до оптических частот, наблюда­ется в твердых, жидких и газообразных веществах.

Ионная поляризация происходит в твердых телах с ионной кристаллической решеткой, выражается в упругом сме­щении ионов относительно узлов решетки, характеризуется τ 10^-12—10^-13 .

Атомная поляризация наблюдается в веществах с валентными кристаллами, у которых атомы соединены в моле­кулы благодаря обменному взаимодействию валентных электро­нов. Времена смещения и релаксации τ=10^-11 - 10^-13 с. Веще­ства с поляризацией смещения характеризуются за редким ис­ключением значениями ε от 4 до 12.

7.3. УДЕЛЬНОЕ СОПРОТИВЛЕНИЕ ОСАДОЧНЫХ ПОРОД

Поскольку удельное сопротивление большинства породооб­разующих минералов осадочных пород на 5—10порядков выше удельного сопротивления пластовой воды р_в, то удельное со­противление породы зависит в основном от р_в, насыщающей, породу, объемной влажности w_B и геометрии пространства, за­нимаемого в породе водой.

7.3.1. УДЕЛЬНОЕ СОПРОТИВЛЕНИЕ ПОЛНОСТЬЮ ВОДОНАСЫЩЕННОЙ ПОРОДЫ

Чистые (неглинистые) породы. Рассмотрим удельное сопро­тивление р_в.ппороды, полностью насыщенной водой, с простей­шей геометрией пор, представленных пучком параллельных ци­линдрических капилляров постоянного сечения. В направлении», совпадающем с направлением осей капилляров, удельное со­противление составит:

Аналогично выражение для удельного сопротивления ρ_в.п породы с извилистыми капиллярами (рис. 36), длина которых в Т_эл раз больше длины капилляров с прямой осью. Величину Т_эл называют электрической извилистостью капилляров в отли­чие от извилистости гидродинамической, рассматриваемой при течении жидкости и газа. Всегда Т_эл≥1. Для породы с простей­шей геометрией пор Т_эл=1; с усложнением геометрии пор Т_эл растет, при этом ρ_в.п при неизменной пористости возрастает пропорционально Т² _эл.

Соотношения (7.16), (7.17) можно записать в виде

где Р_п — электрический параметр пористости, или просто пара­метр пористости, предложенный В. Н. Дахновым, который за­висит от коэффициента пористости и геометрии пор.

Для пород с размером пор больше 0,1 мкм, когда можно пренебречь влиянием ДЭС на поверхности твердой фазы на электропроводность поровых каналов, параметр пористости Р_п является константой данной породы:

которая не зависит от минерализации С_в и удельного сопротив­ления ρ_в воды, насыщающей породу.

Для параметра Р_п пористых сред с различной геометрией порового пространства получены теоретические выражения [1].

Однако геометрия порового пространства реальных осадоч­ных пород настолько сложна и разнообразна, что целесообраз­ность применения теоретических выражений для описания ха­рактера связи между Р_п и k_n весьма ограничена. Для практи­ческих целей удобнее выражать связь между Р_п и k_n эмпири­ческими формулами

где а и т — константы, которые определяют экспериментально для коллекции образцов, представляющей изучаемый геологи­ческий объект.

Величину т называют показателем цементации породы. При а=1 и т=1 выражения (7.20), (7.27) тождественны (7.16). С усложнением геометрии пор т становится больше 1; отличие m от 1 тем больше, чем сложнее геометрия пор.

Зависимости, описываемые выражениями (7.17) и (7.21) изображают прямыми в двойном логарифмическом масштабе. Наклон прямых растет с усложнением геометрии пор, т. е. с ростом т и Т. Зависимости P_n = f(k_n), описываемые формула­ми (7.17) и (7.21), образуют пучок прямых, проходящих через, точку с координатами Р_п=1, k_n=1.

На практике чаще используют зависимость P_n = f(k_n) в виде (7.21). При отсутствии влияния глинистости наиболее характер­ными являются следующие значения т: для хорошо отсорти­рованных песков и слабосцементированных песчаников т=1,3--1,4; для терригенных и карбонатных пород с межзерновой по­ристостью хорошо сцементированных т=1,8--2; для пород с каверново-межзерновой пористостью m>2, причем величина т тем больше, чем выше каверновая составляющая величины k_a и чем больше размеры каверн; для плотных сцементированных пород, содержащих трещины, величина т существенно ниже значения т=1,8--2, характерного для таких пород при отсутст­вии трещин, в пределе т→1.

Удельное сопротивление воды, насыщающей породу, нахо­дят, используя зависимости и приемы, изложенные в подразде­ле 7.2, для известных минерализации, химического-состава рас­творенных солей и температуры раствора.

Минерализация пластовых вод в разрезах нефтяных и газо­вых месторождений изменяется от 5 до 400 г/л. Низкие концент­рации характерны для районов, разрезы которых представлены отложениями эоценового возраста при активном питании их ат­мосферными водами (эоценовые отложения Восточной Грузии).

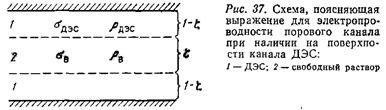
Средние концентрации 15—50 г/л типичны для обширных тер­риторий Западной Сибири, частично Якутии, Северного Кавка­за, Средней Азии, где основную часть разреза представляют мезозойские, частично кайнозойские отложения. Высокие кон­центрации (более 100 г/л) характерны для палеозойских отло­жений на территории Русской и Сибирской платформ. Основ­ным компонентом пластовых вод при любой их минерализации является NaCl. Для вод небольшой концентрации характерно также наличие NaHC0₃ и Na₂S0₄. В водах средней и высокой концентрации появляются СаС1₂, MgCl₂, абсолютное и относи­тельное содержание которых тем больше, чем выше общая ми­нерализация.

Температура пластовых вод изменяется в пределах 10— 230 °С, удельное сопротивление от 0,01 до 1 Ом-м. Примерно в тех же пределах изменяется ρ_к в разрезах угольных месторож­дений.

Глинистые породы. Породы, содержащие глинистые и другие минералы, находящиеся в высоко дисперсном состоянии в при­роде, например, лимонит, цеолиты и др., характеризуются наличием в общем объеме пор субкапиллярных поровых кана­лов, радиус г которых соизмерим с толщиной ДЭС на поверх­ности пор. Поэтому удельное сопротивление полностью водонасыщенных глин и глинистых пород зависит не только от рас­смотренных выше факторов, но и от величины адсорбционной поверхности породы S и соотношения удельных электропроводностей ДЭС σсл и свободного раствора σ_в (рис. 37).

Удельная электропроводность цилиндрического канала σ_Кан, заполненного водой с удельной электропроводностью σ_в, опре­деляется выражением

где ξ— доля объема канала, занимаемая свободным раствором (рис.37).

Величина σ_в= {u+v)C_B. Величина σ_сл подобно σ_в определя­ется как произведение средней эффективности подвижности u_дэс катионов ДЭС на концентрацию поглощенных катионов в объ­еме ДЭС q/{1—ξ):

которое не является константой породы и зависит от величины ρ_в. Отношение фиктивного параметра пористости Р_п.ф к истин­ному Р_п

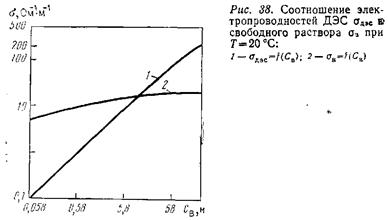
называют коэффициентом поверхностной проводимости. Вели­чина П зависит от соотношения значений σ_в и σ_сл и от доли объема пор, занимаемой ДЭС. Рассмотрим частные случаи.

1. Чистая неглинистая порода, размер пор намного больше σдэс, поэтому ξ=1, Р_п.ф=Рп, П=1, поверхностная проводимость отсутствует.

2. Глина, поровое пространство которой представлено ка­пиллярами с r≈δдэс. ДЭС целиком заполняет капилляры, ξ = 0, Р_п.ф = Р_п σ_в/σ_сл, П= σ_в/σ_сл - В этом случае П=1 только при σ_в=σ_сл , при σ_в > σ_сл П>1; при σ_в < σ_сл П<1.

В электрохимии ДЭС дисперсных систем рассматривается только условие σ_в < σ_сл, когда наличие ДЭС создает дополни­тельную проводимость поровых каналов; в этой области влия­ние ДЭС приводит только к снижению удельного сопротивле­ния пористой среды. Существуют две области значений кон­центрации растворов, в которых соотношение σ_сл и σ_в различ­но [8].

Назовем условно точку пересечения графиков о_Дэс = /(С_в) и σ_в=f(С_в) инверсионной с координатами σ_ин и С_ин (рис. 38). Об­ласть С_в<С_ин соответствует σ_сл> σ_в, при котором справедливы закономерности, установленные в электрохимии дисперсных систем. В области С_В>С_ИН справедливо соотношение о_сл<о_в, при котором наличие ДЭС на поверхности каналов, заполнен­ных свободной водой, приводит к снижению их проводимости σкал и росту удельного сопротивления по сравнению со значениями σ_в и р_в соответственно. Эта закономерность соотношения с_в и σсл была в дальнейшем подтверждена рядом исследователей

Удельное сопротивление в точке инверсии по данным различных авторов составляет 0,2—0,8 Ом-м, поэтому можно говорить о наличии зоны инверсии отношений ρ_в/ρ_Дэ_С и σв/σ_Дэс.

При температуре 20—100 С, характерной для разрезов-большей части известных месторождений нефти и газа, ука­занная область значений р_сл соответствует удельному сопротив­лению растворов NaCl с концентрацией С_в = 0,2—0,5 н (при­мерно 10—25 г/л). Таким образом, области С_В>С_ин, σ_сл<σ_в, ρ_сл>ρ_в

соответствуют условия, характерные для пород нефтя­ных и газовых месторождений, насыщенных пластовыми вода­ми, минерализация которых обычно выше 20 г/л. Следует от­метить, что для значительной части продуктивных отложений Западной Сибири характерны условия, соответствующие инвер­сионной зоне, когда можно принять σ_сл≈σ_в, ρ_сл≈ρ_в . Для зоны проникновения фильтрата промывочной жидкости в породах-коллекторах при бурении скважин на пресном глинистом рас­творе напротив будут типичны условия, характерные для «клас­сической» области поверхностной проводимости: С_ф<С_ич, σ_сл> σ_в, ρ_сл<ρ_в.

Особенности поведения удельного сопротивления ρ_п._гл и фик­тивного параметра пористости Р_п.ф глинистых пород и суспензий при изменении в широких пределах коэффициента пористости k_n (для суспензий — объемной влажности), концентрации свобод­ного раствора С_в, размера частиц а и, следовательно, адсорб­ционной способности глинистого материала Q рассмотрим на примере расчетных графиков Р_п._ф=f(k_п) для различных С_в = = const при а = const для каждого семейства и Р_п._ф=f(k_п) для. различных a = const при C_B = const для каждого семейства (рис.39).

Расчетные графики Р_п._ф=f(k_п) получены для модели «моно­минеральной глины», образованной кубическими частицами по-
стоянного размера а, расположенными по кубической сетке с постоянной шириной щелевидных пор, разделяющих слои куби­ков. Величина k_n изменяется в пределах 1>k_п>k_{п min}, Где k_{п min} — предельно уплотненная «глина», для которой ширина щелей h между рядами кубиков уменьшаясь достигает двойной толщины монослоя h_min=2δсл- Изменение k_n в таких пределах охватывает весь спектр глинистых дисперсных систем, включа­ющий глинистые суспензии, глинистый неуплотненный осадок, уплотненные в разной степени глины. Величина k_{п min}, опреде­ляемая отношением h_min/a, тем больше, чем меньше размер частиц а. Изменение а в пределах 5<а<5000 нм позволяло имитировать глинистые минералы с различной дисперсностью и обменной адсорбционной способностью твердой фазы 2,3<Q< <23 мг-экв/r. Модели «насыщались» раствором NaCl, кон­центрация которого изменялась в пределах 0,001—4 н., а значе-

ния ρ_в и σ_в при Т=20°С соответственно в пределах 0,05— 94 Ом•м и 0,106—200 Ом^-1•см^-1.

Значение ρ_п._гл рассчитывалось по формуле

Величина Р_п вычислялась в соответствии с заданным k_п по формуле В. Н. Дахнова для модели пористой среды с кубиче­скими зернами [1, 13]. Величина ρ_КАН рассчитывалась по фор­муле (7.25), в которую подставлялось значение ξ, вычисленное в соответствии с отношением σ_сл/h. Величина σ_сл определялась по графику σ_сл = f(С_в) (см. рис. 38).

Значение Р_п.ф вычислялось по формуле

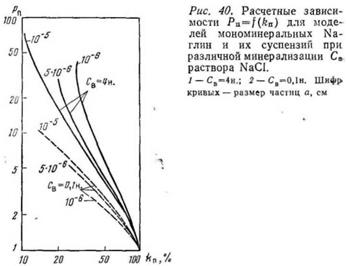
Несмотря на упрощающие предположения о форме глинистых частиц, геометрии порового пространства и т. д., расчетные гра­фики Р_п.ф = f(k_п) находятся в удовлетворительном соответствии с экспериментальными, полученными различными исследова­телями на искусственных образцах мономинеральных глин (см. рис. 39 и 40).

Анализ расчетных кривых позволяет отметить следующее.

1. Во всем диапазоне изменения k_n с уменьшением концент­рации С_в свободного раствора, насыщающего глину или явля­ющегося водной фазой суспензии, величина Р_п.ф уменьшается. Степень снижения Р_п.ф тем больше, чем выше дисперсность глины.

2. Большая часть кривых Р_п.ф = f(k_п) характеризуется моно­тонным ростом Р_п.ф с уменьшением k_n при С_в = const. Кривые

3. Р_пф = f(k_п) для значений С_в≤0,002 н и глин низкой дисперсно­сти, для значений С_в≤0,02 н и глин высокой дисперсности име­ют аномальную форму: в области высоких k_п (суспензии и гли­нистые неуплотненные осадки) с уменьшением k_п значение Р_пф уменьшается, достигая минимума, после чего растет. При этом значительная часть кривой расположена в области Р_пф <1. Такое явление «сверхпроводимости» глинистых частиц в пресных растворах объясняется тем, что при определенных со­отношениях дисперсности глины и концентрации свободного раствора снижение удельного сопротивления дисперсной систе­мы за счет высокой электропроводности σ_сл>>σ_в ДЭС на поверх­ности частиц преодолевает противоположное влияние, обуслов­ливающее рост удельного сопротивления системы по сравнению с р_в благодаря замещению части объема практически непрово­дящими частицами глины.

4. 3. Закономерность изменения Р_пф с изменением дисперснос­ти глины при С_в = const различна в зависимости от области концентрации С_в. Так, при С_в = 4н и 1н графики зависимости Р_пф = f(k_п) для глины с меньшей дисперсностью располагаются ниже зависимости Р_пф = f(k_п) для глины с большей дисперсно­стью. При С_в≤0,1 н., напротив, графики Р_пф = f(k_п) для высо­кодисперсных глин расположены ниже графиков для глин мень­шей дисперсности. При С_в≈0,2 н. значения Р_п.ф≈Р_п. Поэто­му для глин любой дисперсности график Pn = f(k„) практически один и тот же. Вид его определяется влиянием только геометрии пор, влияние электрохимического фактора отсутствует.

5. Получены также расчетные графики для модели глинистой породы, в частности глинистого коллектора с рассеянной глини­стостью. Параметр Р_пф рассчитывали по формуле

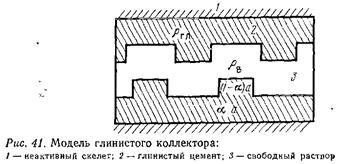
6. где Рп.ск — параметр пористости чистого минерального скеле­та, не содержащего глинистых частиц; р₃ — удельное сопротив­ление среды, заполняющей неактивный скелет, образованной смесью агрегатов глинистых частиц (глинистый цемент) и сво­бодной воды. Величина р₃ зависит от удельного сопротивления глинистых агрегатов и свободного раствора р_в, степени заполне­ния глинистым материалом пространства между скелетными зернами, а также от геометрии участков, занимаемых глиной и водой, и их взаимного расположения.

7. В качестве модели чистого скелета принят трехмерный иде­альный грунт с расположением капилляров в трех взаимно-перпендикулярных направлениях; величину Р_п.ск рассчитывали по соответствующей формуле для заданных k_п.ск. Модель за­полнения скелета представлена обособленными участками, за­нимаемыми глинистыми агрегатами и свободной водой; часть

8. глинистого материала расположена параллельно участкам, за нимаемым водой, часть — последовательно с ними (рис. 41). Величину р₃ рассчитывали по формуле

9.

10.где α — доля глинистого материала, размещенного последова­тельно с раствором; а — степень заполнения глинистым мате­риалом пустот чистого скелета. В формулу (7.30) подставляли

_11. расчетные или экспериментальные значения ρ_гл для заданных ρ_в, k_п.гл, Q_гл

12.Величина коэффициента пористости модели глинистого кол­лектора с рассеянной глинистостью

13.

14.Расчетные зависимости Р_пф= f(k_п) для k_п.ск=0,3 и глинисто­го материала различной дисперсности, полученные при различ­ных ρ_в = const, охватывают интервал k_п=0,18--0,3 для пород-коллекторов с различным содержанием глинистого материала, которое имитируется изменением а в пределах 0—1, соответст­вующих чистому коллектору и глинистой породе-неколлектору.

15.Зависимости Р_пф= f(k_п) характеризуются следующими осо­бенностями (рис. 42).

16.Наблюдается закономерное снижение Р_пф с уменьшением С_в при постоянной дисперсности глинистого материала, как и для моделей чистых мономинеральных глин. Степень снижения тем больше, чем больше активность Q глины. В области С_в> >0,2н. дисперсия зависимостей Pn = f(k„) для различных С_в и Q невелика. Эта дисперсия существенно возрастает при С_в< <0,2н., а при С_в<0,01 н. величина Pn уменьшается при сни­жении k_n, что объясняется рассмотренным выше эффектом сверхпроводимости глинистых частиц в пресных растворах. В области С_в>0,2н. значения Р_пф>Р_п.ск, в области С_в<0,2н. значение Р_пф<Р_п.ск Следовательно, при С_в>0,2 н. присутст-

вие в породе глины вызывает увеличение Р_пф по сравнению с Р_п.ск для чистой породы, а при С_в<0,2н — уменьшение Р_Пф по отношению к Р_п.ск. Влияние глинистости тем больше, чем выше ее дисперсность.

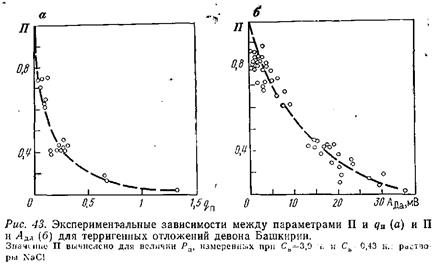
Рассмотренные закономерности поведения зависимостей Р_пф= f(k_п) подтверждены обширным фактическим материалом, полученным для реальных глинистых пород-коллекторов. Ин­версионное значение С_в и соответствующее ему р_в для коллекто­ров с различным составом глинистого цемента, обменного катионного комплекса глин и при различной температуре меняют­ся в пределах: С_в = 0,24-0,5 н. и ρ_в= 0,2—0,8 Ом-м [8, 25, 36].

Учитывая это обстоятельство, рекомендуется в качестве коэффициента поверхностной проводимости породы как характе­ристики влияния глинистости на связь Р_пф= f(k_п) использовать параметр П:

П = Р_пф /Р_п.пред(7.32)

где Р_п.пред — предельное (максимальное) значение параметра пористости, соответствующее удельному сопротивлению породы при насыщении ее высокоминерализованной водой. Рассчитан­ная по формуле (7.32) величина П≤1. Значение П тесно связа-

но с приведенной емкостью обмена q_n и диффузионно-адсорбци­онной активностью А_да породы (рис. 43).

Все три параметра характеризуют адсорбционную способ­ность породы. Для пород с различным содержанием глинистого материала постоянного минерального состава наблюдается так­же тесная связь П и η_гл. Для определения величины П состав­лены палетки в виде семейства кривых П = f(ρ_в) для различных q_n = const или η_гл = const, позволяющие найти П при известных ρ_в и характеристиках глинистости породы q_n или η_гл (рис. 44). Для использования при интерпретации материалов ГИС удоб­ны палетки, представленные семейством графиков П = f(ρ_в) для различных α_сп = const, где относительная амплитуда α_сп играет роль параметра глинистости.

Трещиноватые, кавернозные и трещиновато-кавернозные по­роды. Рассмотрим породу, где все трещины имеют границы в виде гладких параллельных плоскостей. Если блоки породы, между которыми расположены трещины, представлены непро­водящим минеральным скелетом, коэффициент пористости та­кой породы равен отношению суммарного объема трещин к объему породы, т. е. коэффициенту трещиноватости k_т. Удель­ное сопротивление полностью водонасыщекной трещиноватости породы с одной системой параллельных трещин, расположен­ных по направлению тока,

Расчет Р_пт по формуле (7.38) для 0,5<А<1показывает, что графики зависимостей Р_пт = f (k_п) для различных k_T = = const располагаются ниже графиков зависимостей Р_п.бл = f(k_п.мз)-Причем отличие Р_п._т от Р_п.бл тем больше, чем выше k_T. Величина k_T реальных трещиноватых пород не превышает 0,01.Поэтому расчеты выполнены для 0<kт<0,01.Влияние трещин существенно для низкопористых пород при k_п<0,1и при k_T = const возрастает с уменьшением k_n. В породах средней и высокой пористости влияние трещин при реальных значениях k_r пренебрежимо мало (рис. 45).

При заполнении трещин водным раствором более пресным, чем вода, насыщающая блоки, так, что удельное сопротивле­ние раствора в трещинах ρ_ф ≥10ρ_в,величина р_п._т определяется выражением

Влияние трещин на величину р_п._т уменьшается и при ρ_ф →ρ_п.бл исчезает. Те же закономерности справедливы и при за­полнении трещин смесью воды и углеводородов с удельным со­противлением р_ом.

Породу с каверновой пористостью можно представить как минеральный скелет, в котором регулярно по определенной сис­теме или хаотически распределены каверны, заполненные рас­твором с удельным сопротивлением р_в. Такая порода имеет р_пк = ∞, поскольку проводящие участки среды — каверны — разобщены непроводящим материалом. В геологических разре­зах присутствие такой породы маловероятно. Реальные каверновые породы представлены обычно блоками с межзерновой пористостью k_п.мз содержат каверны различного размера, боль­шего размеров межзерновых пор. Каверны и межзерновые поры насыщены водным раствором с удельным сопротивлением р_в. Удельное сопротивление такой породы определяется выраже­нием

где k_кав — коэффициент каверновой пористости или кавернозности, равный суммарному объему каверн в единице объема породы.

поскольку коэффициент межзерновой пористости блоков указы­вается по отношению к объему блоков, а не к всему объему по-

Коэффициент общей пористости такой породы

Параметр пористости кавернозной породы Р_п.к = ρ_п.к/ρ_в выше значения Р_п для породы с межзерновой пористостью, значение k_n которой определяется выражением (7.41). Расчетные кривые Р_п.к =f(k_п) для различных k_кав = const располагаются выше за­висимости Р_п.бл = f (kп.мз)- При ПОСТОЯННОМ ЗНЭЧеНИИ k_кав отличие Р_п.к от Р_п возрастает с уменьшением k_n. Такое влияние ка­верн на величины ρв.п.к и Р_п.к объясняется усложнением геомет­рии токовых линий в каверне и, следовательно, возрастанием их извилистости Тэл по сравнению с извилистостью линий тока в межзерновых порах.

Не нашли, что искали? Воспользуйтесь поиском по сайту: