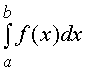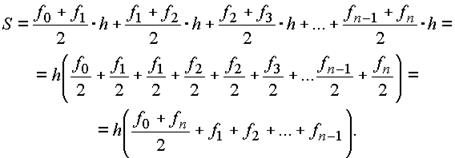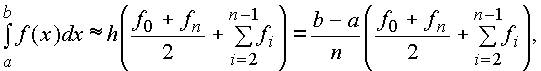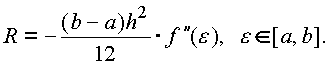|
|
Решение с помощью MS ExcelСодержание Введение. 2 Задание 1. 3 Общие сведения о решении нелинейного уравнения. 3 Отделение корней. 3 Метод итераций. 4 Решение задания в MS Excel 5 Решение в Mathcad. 7 Задание 2. 15 Решение с помощью MS Excel 18 Решение с помощью Mathcad. 20 Задание 3. 21 Канонический полином. 22 Полином Лагранжа. 23 Полином Ньютона. 24 Решение при помощи MS Excel 24 Листинг пользовательских функций. 25 Решение при помощи Mathcad. 27 Заключение. 29 Список использовааных источников. 30 Введение Современное развитие физики и техники тесно связано с использованием электронных вычислительных машин (ЭВМ). В настоящее время ЭВМ стали обычным оборудованием многих институтов и конструкторских бюро. Это позволило от простейших расчетов и оценок различных конструкций или процессов перейти к новой стадии работы - детальному математическому моделированию (вычислительному эксперименту), которое существенно сокращает потребность в натурных экспериментах, а в ряде случаев может их заменить. Сложные вычислительные задачи, возникающие при исследовании физических и технических проблем, можно разбить на ряд элементарных -таких как вычисление интеграла, решение дифференциального уравнения и т. п. Многие элементарные задачи являются несложными и хорошо изучены. Для этих задач уже разработаны методы численного решения, и нередко имеются стандартные программы решения их на ЭВМ. Есть и достаточно сложные элементарные задачи; методы решения таких задач сейчас интенсивно разрабатываются. В связи с этим современный специалист с высшим образованием должен обладать не только высоким уровнем подготовки по профилю своей специальности, но и хорошо знать математические методы решения инженерных задач, ориентироваться на использование вычислительной техники, практически освоить принципы работы на ЭВМ.
Задание 1
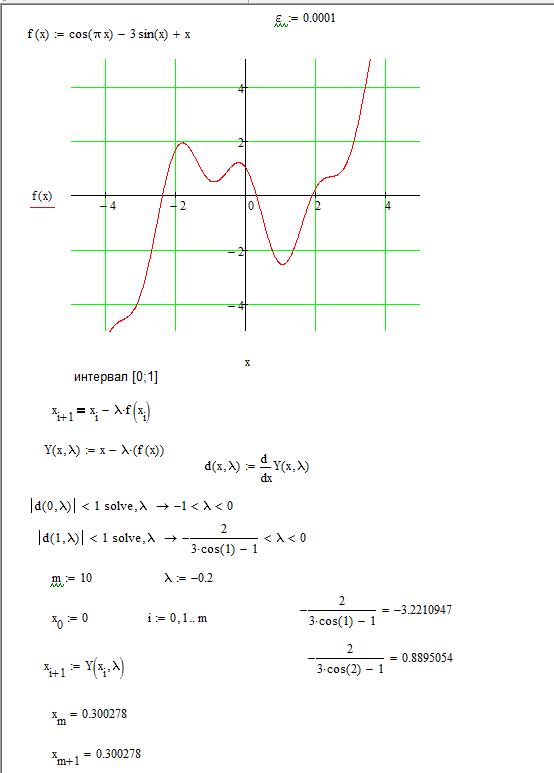
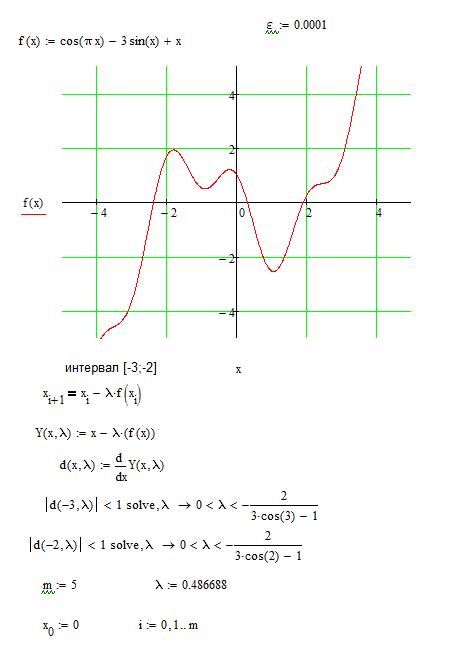
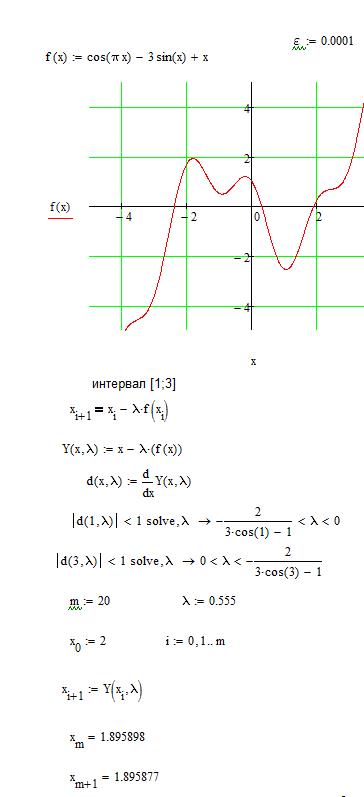
Заданная функция Поиск корней функции методом итераций. Заданная точность 0,0001. Определить количество итераций для достижения требуемой точности.
Общие сведения о решении нелинейного уравнения Как правило, нелинейное уравнения общего вида f(х)=0 невозможно решить аналитически. Для практических задач достаточно найти приближенное значение x, в определенном смысле близкое к точному решению уравнения хточн. В большинстве случаев поиск приближенного решения включает два этапа. На первом этапе отделяют корни, т. е. находят такие отрезки, внутри которых находится строго один корень. На втором этапе уточняют корень на одном из таких отрезков, т.е. находят его значение с требуемой точностью. Достигнутая точность может оцениваться либо «по функции» (в найденной точке x, функция достаточно близка к 0, т.е. выполняется условие |f(x)|≤ ef, где ef требуемая точность по оси ординат), либо «по аргументу» (найден достаточно маленький отрезок [a,b], внутри которого находится корень, т.е. |b–a|≤ ex, где ex требуемая точность по оси абсцисс). Отделение корней Отделение корней может производиться сочетанием графического и аналитического исследования функции. Такое исследование опирается на теорему Вейерштрасса, в соответствии с которой для непрерывной на отрезке [a,b] функции f(х) и любого числа y, отвечающего условию f(a)≤y≤f(b), существует на этом отрезке точка x, в которой функция равна y. Следовательно, для непрерывной функции достаточно найти отрезок, на концах которого функция имеет разные знаки, и можно быть уверенным, что на этом отрезке есть корень уравнения f(х)=0. Для ряда методов уточнения желательно, чтобы найденный на первом этапе отрезок содержал только один корень уравнения. Это условие выполняется, если функция на отрезке монотонна. Монотонность, можно проверить либо по графику функции, либо по знаку производной. Метод итераций Для применения этого метода исходное уравнение f(x)=0 преобразуют к виду: x=y(х). Затем выбирают начальное значение х0 и подставляют его в левую часть уравнения, получая, в общем случае, x1=y(х0) ¹ х0¹ y(х1), поскольку х0 взято произвольно и не является корнем уравнения. Полученное значение х1 рассматривают как очередное приближение к корню. Его снова подставляют в правую часть уравнения и получают следующее значение х2=y(х1)). Расчет продолжают по формуле хi+1=y(хi). Получающаяся таким образом последовательность: х0, х1, х2, х3 х4,... при определенных условиях сходиться к корню хточн. Можно показать, что итерационный процесс сходится при условии |y’(x) | < 1 на [a, b]. Существуют различные способы преобразования уравнения f(x) = 0 к виду y(х) = х, причем в конкретном случае одни из них приведут к сходящемуся, а другие – к расходящемуся процессу вычислений. Один из способов, заключается в применении формулы
причем k следует выбирать так, чтобы | k | > Q/2, где Q = max|f’(x)| на отрезке [a, b] и знак k совпадал бы со знаком f’(x) на [a, b]. Точность вычислений можно оценить из соотношения
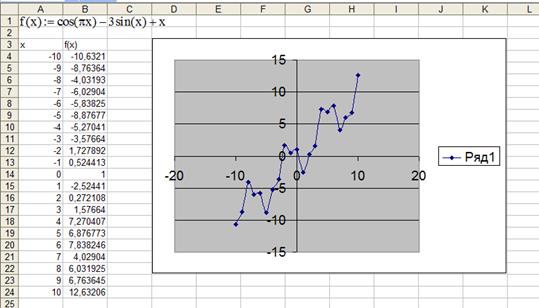
где М = max |y’(x)| на [a, b]. Когда желаемый результат вычислений по формуле известен, но неизвестны значения, необходимые для получения этого результата, можно воспользоваться средством Подбор параметра, выбрав команду Подбор параметра в меню Сервис. При подборе параметра Excel изменяет значение в одной конкретной ячейке до тех пор, пока вычисления по формуле, ссылающейся на эту ячейку, не дадут нужного результата. При подборе параметра Excel использует итерационный (циклический) процесс. Количество итераций и точность устанавливаются в меню Сервис/Параметры/вкладка Вычисления. Если Excel выполняет сложную задачу подбора параметра, можно нажать кнопку Пауза в окне диалога Результат подбора параметра и прервать вычисление, а затем нажать кнопку Шаг, чтобы выполнить очередную итерацию и просмотреть результат. При решении задачи в пошаговом режиме появляется кнопка Продолжить - для возврата в обычный режим подбора параметра. Решение задания в MS Excel Составили таблицу значений функции на интервале от -10 до 10. Построили график функции как показано на рис. 1.
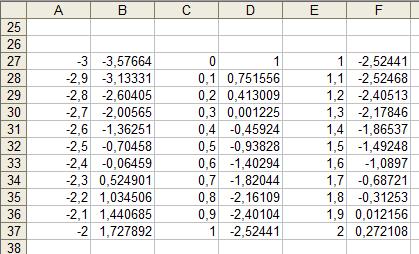
Рисунок 1 – Таблица значений и график функции Разбили первоначальный интервал на отрезки: [-3;-2] [0;1] [1;2] и создали таблицы значений функции на каждом интервале как показано на рис. 2.
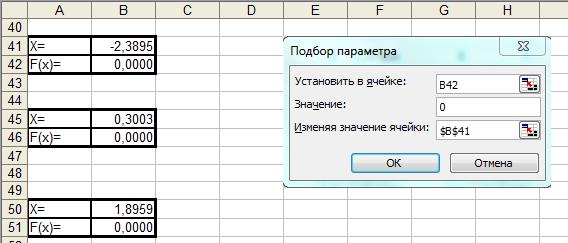
Рисунок 2 – Разбиение на отрезки Выявили, при каких значениях аргумента функция меняет знак на противоположный. Эти значения применяли для определения корней функции методом подбора параметра, как показано на рис. 3.
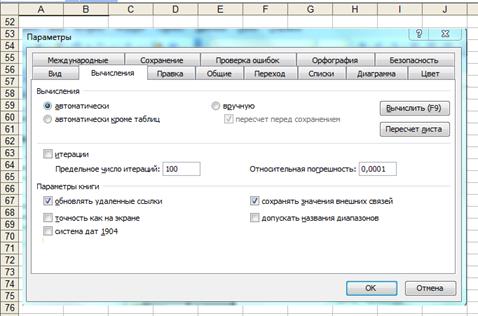
Рисунок 3 Применение подбора параметра для нахождения корней функции Требуемую точность устанавливали в Параметры-Вычисления как показано на рис. 4.
Рисунок 4 – Изменение значения погрешности вычисления
Решение в Mathcad Процесс решения задания представлен ниже на рисунках. Рассмотрели график функции, выявили интервалы, в которых функция меняет знак на противоположный, определили корни на каждом промежутке, определили погрешность и проверили решение стандартной функцией root.
Задание 2 2) Определение площадей фигур: а) ограниченной осью ОХ, функцией f(x), на отрезке [первый корень функции; второй корень функции] б) ограниченной осью ОХ, функцией f(x), на отрезке [второй корень функции; третий корень функции] методом трапеции с точностью 0,001. Какое должно быть разбиение для достижения требуемой точности?
С геометрической точки зрения определенный интеграл
Чтобы приближенно вычислить эту площадь, разделим интервал интегрирования
Можно повысить точность вычисления определенного интеграла, если заменить на каждом интервале
Метод трапеций. Величина определенного интеграла численно равна площади фигуры, образованной графиком функции и осью абсцисс (геометрический смысл определенного интеграла).
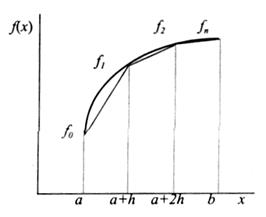
Следовательно, найти – это значит оценить площадь фигуры, ограниченной перпендикулярами, восстановленными к графику подынтегральной функции f(x) из точек a и b, расположенных на оси аргумента x. Для решения задачи разобьем интервал [a,b] на n одинаковых участков. Длина каждого участка будет равна h=(b-a)/n (см. рис. 1).
Рисунок 5 – Определение площади методом трапеции .
Восстановим перпендикуляры из каждой точки до пересечения с графиком функции f(x). Если заменить полученные криволинейные фрагменты графика функции отрезками прямых, то тогда приближенно площадь фигуры, а следовательно и величина определенного интеграла оценивается как площадь всех полученных трапеций. Обозначим последовательно значения подынтегральных функций на концах отрезков f0, f1, f2,..., fn и подсчитаем площадь трапеций
В общем случае формула трапеций принимает вид
где fi – значение подынтегральной функции в точках разбиения интервала (a,b) на равные участки с шагом h; f0, fn – значения подынтегральной функции соответственно в точках a и b. Остаточный член пропорционален длине интервала [a,b] и квадрату шага h
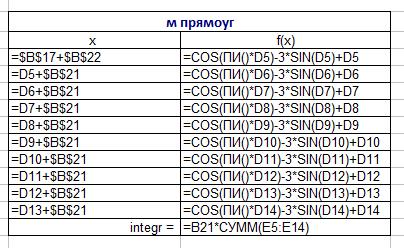
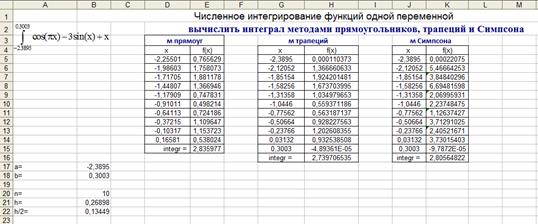
Точность вычисления определенного интеграла повышается с уменьшением шага h (увеличением числа отрезков n). Решение с помощью MS Excel Создали расчетные таблицы, в ячейки как показано на рисунках ниже ввели формулы, получили расчетные таблицы и ответы для методов прямоугольника, трапеции, Симпсона.
Рисунок 6 – Формулы для метода прямоугольника
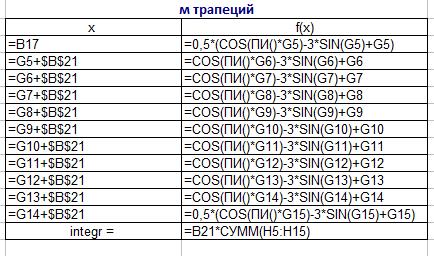
Рисунок 7 – Формулы для метода трапеций
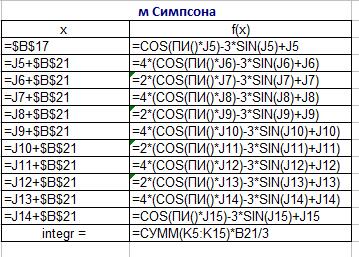
Рисунок 8 – Формулы для метода Симпсона
Рисунок 9 – Общий вид на формулы в окне MS Excel
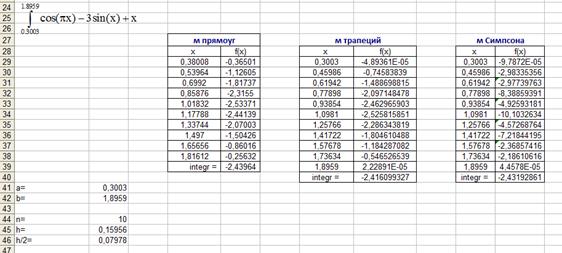
Рисунок 10 – Результат расчета первого интеграла
Рисунок 11 – Результат расчета второго интеграла
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
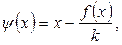
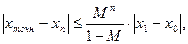
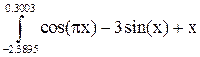
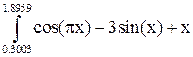
– есть площадь фигуры, ограниченной графиком функции 
и прямыми 
, 
, 
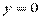. Функция 
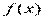называется подынтегральной функцией.
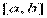на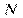 
равных отрезков длиной 
каждый. Тогда координата левого конца i-го отрезка определяется по формул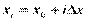е 
, где 
, 
. Простейший приближенный расчет площади под кривой 
, а высота равна значению функции в точке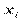 
(метод левых прямоугольников). Можно высоту брать равной значению функции в точке 
(метод правых прямоугольников) или в точке 
(метод центральных прямоугольников). При использовании метода левых прямоугольников формула для вычисления площади выглядит следующим образом:
.
, 
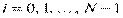дугу графика 
отрезком (хордой), соединяющем точки с координатами 
и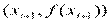 
. В этом случае фигура, ограниченная графиком функции и прямыми 
, 
, приближенно заменяется не прямоугольником, а трапецией, и искомый определенный интеграл рассчитывается как сумма площадей всех таких трапеций:
.
