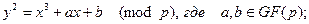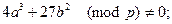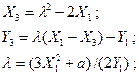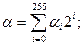|
|
Основные теоретические положения.12
Эллиптической кривой (ЭК) называется уравнение вида:
После наложения ограничений на множество значений переменных х,y и коэффициентов a и b, получается эллиптическая кривая, заданная над определенным числовым множеством (полем). Применительно к криптографии, эллиптическую кривую можно определить как множество пар х,y Î GF(p), удовлетворяющих уравнению
Данные пар (х,y) называют точками. Поскольку данные точки представляют абелеву группу, над ними справедливы операции сложения, вычитания и умножения. Кроме того существует особая нулевая точка эллиптической кривой, получаемая путем сложения двух произвольных точек эллиптической кривой P(хp,yp) Q(хq,yq), в случае, если xp = xq, yp = - yq, Нулевая точка считается бесконечно удаленной точкой ЭК. Возможность определения конечной абелевой группы на точках ЭК, и выполнения над ними операций сложения и умножения, делает эллиптические кривые весьма полезными в криптографических приложениях. Рассматриваемая криптосистема базируется на проблеме дискретного логарифма эллиптической кривой (Elliptic Curve Discrete Logarithm Problem – ECDLP). Данная проблема формулируется следующим образом: «Даны образующая поля – точка Р и расположенная на кривой точка kP; найти значение k» Для достаточно больших полей точек ЭК, решение данного уравнения представляет значительную трудность. При выборе коэффициентов а и b для криптосистем, основанных на ЭК следует учитывать, что они должны удовлетворять условию:
При этом оценить общее количество точек поля ЭК можно в соответствие с формулой:
Прежде, чем производить расчеты в поле группы точек, в соответствии с рекомендациями ГОСТ 34.10 – 2001, необходимо дополнительно выбрать простое число q – порядок циклической подгруппы группы точек ЭК, для которого должны выполняться следующие условия:
Таким образом, после выбора образующей поля P(хp,yp) и числа q должно выполняться равенство :
Операции сложения точек ЭК должны выполняться по формулам:
А) Правило сложения точек:
Для всех (X1,Y1) Î E(GF(p)) и (X2,Y2) Î E(GF(p)), удовлетворяющих условию X1≠ X2, (X1,Y1) + (X2,Y2) = (X3,Y3) , где значения X3 и Y3 вычисляются по формулам:
Б) Правило удвоения точки:
Для всех (X1,Y1) Î E(GF(p)), удовлетворяющих условию Y1≠ 0 2(X1,Y1) = (X3,Y3) , где
Методика выполнения работы
Задание на выполнение лабораторной работы выдается преподавателем после прохождения студентами собеседования по основам криптографической защиты информации.
Схема алгоритма шифрования с использованием эллиптических кривых.
3.1.1. Задаемся модулем эллиптической кривой р и в соответствии с условием:
выбираем коэффициенты а и b данной ЭК. 3.1.2. Согласно формуле:
производим оценку порядка точек m эллиптической кривой. 3.1.3. Согласно соотношениям:
выбираем q– порядок циклической подгруппы группы точек ЭК. 3.1.4. Образующую поля, точку P(хp,yp), выбираем исходя из соотношения:
3.1.5. Выбираем случайное число k, являющееся секретным ключем данной криптосистемы. 3.1.6. Производим вычисление точки kP = Pk(xk, yk). 3.1.7. По формуле
Производим преобразование входного двоичного вектора в целое число a, и вычисляем точку aP = Pa (Xa, Ya).
3.1.8. Вычисляем Pk(xk, yk) + Pa (Xa, Ya) = Q(X,Q, YQ). Полученная точка Q(X,Q, YQ) является зашифрованным представлением исходного числа a, а величина k – секретным ключем данной криптосистемы. 3.1.9. Для дешифрования необходимо зная секретный ключ k, получить точку Pk(xk, yk), после чего вычислить Q(X,Q, YQ) - Pk(xk, yk) = Pa (Xa, Ya).
Пример расчета.
4.1. Задаемся модулем эллиптической кривой р, а также коэффициентами а и b : p = 29, a = -1, b = 1. 4.2. Проверяем корректность выбора коэффициентов:
4a3 + 27b2 mod 29 = 23 ¹ 0; 4.3. Производим оценку порядка точек в поле:
29 + 1 - 2Ö29 £ m £ 29 + 1 + 2Ö29 19,23 £ m £ 40,7 20 £ m £ 40
4.4. Выбираем q, пользуясь соотношением:
m = nq, при n = 1, q = m/n = 37.
4.5. Выбираем секретный ключ k = 3, и образующую поля P1(0,3) 4.6. Вычисляем:
kP0 = P0 + P0 + P0 = 2 P0 + P0 = P3(1,34) 4.7. Пусть входной вектор a равен 2, тогда 2 P0 = P2(36,3) 4.8. Вычисляем: P3(1,34) + P2(36,3) = P5(9,27) Точка P5(9,27) является зашифрованным представлением входного вектора a
4.9. Для расшифрования необходимо вычислить P5(9,27) - P3(1,34) = P2(36,3)
Мы получили исходную точку, соответствующую расшифрованному входному вектору. 5. Содержание отчета.
5.1. Цель и назначение работы 5.2. Общие теоретические положения 5.3. Описание алгоритма шифрования с использованием ЭК 5.4. Результаты расчетов по исходным данным, предоставленным преподавателем 5.5. Выводы по работе.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|