|
|
Расположение электронов в атоме12 Глава 1. Строение и взаимодействие атомов и молекул Одним из величайших достижений естествознания на рубеже XIX иXX вв. стало доказательство того факта, что все вещества в окружающем нас мире и мы сами построены из атомов и молекул – маленьких частиц, которые находятся в беспрерывном движении, притягиваются на небольших расстояниях друг от друга, но отталкиваются, если одну из них плотнее прижать к другой. По современным представлениям молекула – это наименьшая частица вещества, способная к самостоятельному существованию и обладающая всеми химическими свойствами данного вещества. Мы окружены молекулами и большая часть того, с чем мы соприкасаемся, построена из молекул. Молекулы представляют собой характерные сочетания из нескольких атомов, связанных друг с другом достаточно прочными химическими связями. Атомы одного сорта называют химическим элементом. Таким образом, атом – это наименьшая частица химического элемента, обладающая всеми химическими свойствами данного элемента. Долгое время атомы никто не видел, а их изучение осуществлялось косвенными методами. С помощью спектроскопии, т.е. изучения света, поглощаемого и излучаемого атомами и молекулами, удалось сделать выводы о внутренней структуре атомов и выяснить расположение атомов в отдельных молекулах. Методом дифракции рентгеновских лучей были рассчитаны плотности распределения связанных с атомами электронов. Однако значительные успехи электронной микроскопии привели, наконец, к долгожданной цели – ученым удалось получить изображения индивидуальных атомов и молекул (рис.1.1). Размеры и массы атомов чрезвычайно малы. По порядку величины они равны 10–8 см и 10–24 г соответственно. Но, несмотря на свою чрезвычайную малость, эти числа не произвольны: именно такие малые диаметры и массы нужно приписать атомам и молекулам, чтобы свойства веществ, которые из них состоят, оказались такими, какими мы их наблюдаем в природе. Ну, а коль скоро свойства веществ определяются, в конечном итоге, свойствами атомов, изучение строения и свойств твердых тел мы начнем с обзора сведений о строении отдельных атомов и с изучения свойств атомов, расположенных внутри веществ.
Строение и химические свойства атомов Еще в 1909 г., после опытов великого английского физика Эрнеста Резерфорда по рассеянию падающих на металлическую фольгу a-частиц, стало ясно, что атомы состоят из плотного положительно заряженного ядра и электронного облака, образованного движущимися вокруг ядра электронами. Из чего же состоит атомное ядро и как в пространстве вокруг ядра распределены атомные электроны? Строение атомного ядра Размеры атомного ядра примерно в 100000 раз меньше размеров атома. В состав ядра входят положительно заряженные протоны, масса которых приблизительно равна 1,67×10–27 кг, и не имеющие заряда нейтроны с массой около 1,68·10–27 кг. Эти частицы удерживаются в ядре благодаря сильному ядерному взаимодействию. Суммарное число A протонов и нейтронов в ядре называется массовым числом. Это число определяет массу атома, так как практически вся масса атома сосредоточена в его ядре.
Заряд ядра определяется числом Z входящих в его состав протонов. Это число называют зарядовым числом. Заряд ядра равен суммарному заряду атомных электронов Ze, благодаря чему свободные атомы электронейтральны. Расположение электронов в атоме Атомные электроны с большой скоростью движутся в пространстве вокруг ядра. Нельзя точно сказать, в какой точке этого пространства находится электрон в данный момент времени. Можно говорить лишь о вероятности нахождения электрона на определенном расстоянии от ядра. Область пространства вблизи атомного ядра, в которой вероятность нахождения электрона является наибольшей, называется орбиталью (рис.1.2). Последовательное описание распределения электронов вблизи атомного ядра возможно только в рамках квантовой механики (приложения 1 и 2). В квантовой механике вероятность нахождения электрона на определенном расстоянии от ядра задается квадратом волновой функции, которая является решением основного уравнения квантовой механики – уравнения Шрёдингера. При этом оказывается, что эта вероятность, другими словами, состояние электрона в атоме описывается четырьмя квантовыми числами: главным квантовым числом n, орбитальным квантовым числом l, магнитным квантовым числом m и спиновым квантовым числом s. Главное квантовое число n определяет размер электронного облака и характеризует величину энергии электрона. В атоме водорода (Z=1), например, или в водородоподобном ионе с зарядом ядра +Ze значение энергии электрона определяется выражением:
где m – масса электрона, e0– электрическая постоянная, h – постоянная Планка.
Главное квантовое число может принимать любое положительное целочисленное значение, большее или равное единице: n = 1, 2, 3, … Таким образом, энергия электрона в атоме может принимать только дискретный набор значений, каждое из которых отвечает определенному энергетическому уровню атома. Наименьшей энергией обладают электроны первого энергетического уровня (n = 1); они наиболее прочно связаны с ядром. Электроны последующих уровней характеризуются большим запасом энергии. Набор дискретных значений энергии атомных электронов называют энергетическим спектром атома. Орбитальное квантовое число l описывает форму (симметрию) орбиталей и характеризует величину орбитального момента импульса атомного электрона:
Оно может принимать целочисленные значения от 0 до n–1: l = 0, 1, 2, …, (n–1). Таким образом, орбитальный момент электронов в атоме, также как и их энергия, квантуется, то есть может принимать дискретный набор значений. Обычно для обозначения состояний электронов, отвечающих различным значениям орбитального квантового числа, и соответствующих орбиталей применяют строчные буквы латинского алфавита: s (l=0), р (l=1), d (l=2), f (l=3) и т.д. (Форма s- и р- орбиталей приведена на рис.1.2.) Буквы s, p, d, f берут начало от наименования серий в спектрах щелочных металлов: s - sharp (резкая), p - principal (главная), d - diffuse (диффузная), f - fundamental (фундаментальная). Буквы, следующие за f, идут в алфавитном порядке. Энергия электрона (1.1) в атоме водорода не зависит от значения орбитального квантового числа l. Иными словами, энергетический спектр электрона в атоме водорода вырожден по орбитальному квантовому числу. Однако это вырождение является случайным. Оно характерно только для кулоновского потенциала взаимодействия электрона с атомным ядром и носит название кулоновского вырождения. В случае многоэлектронных атомов или ионов благодаря дополнительному взаимодействию электронов друг с другом это вырождение снимается, поэтому электроны с различными орбитальными квантовыми числами (s-электроны, р-электроны и т. д.) обладают различной энергией: их энергия тем больше, чем больше значение l, точнее, сумма (n+l).
А) б)
Рис. 1.3.Энергетический спектр электрона в атоме водорода (а) вырожден по орбитальному квантовому числу. Однако в многоэлектронных атомах или ионах благодаря дополнительному взаимодействию электронов друг с другом это вырождение снимается (б), и уровни энергии, отвечающие определенному значению главного квантового числа, расщепляются на подуровни, соответствующие различным значениям орбитального квантового числа.
Этот факт может быть выражен следующей эмпирической формулой
где Dl – малая добавка, величина которой зависит от значения орбитального квантового числа l. Таким образом, в многоэлектронных атомах уровни энергии, отвечающие определенному значению главного квантового числа n, расщепляются на подуровни, соответствующие различным значениям орбитального квантового числа l(рис.1.3). На зависимость энергии электронов в многоэлектронных атомах от орбитального квантового числа впервые обратил внимание ученых известный немецкий физик Арнольд Иоганн Вильгельм Зоммерфельд. В 1916 г. он теоретически предсказал, что энергии электронов, движущихся вокруг атомного ядра по орбитам с одинаковым n, но разными l, должны немного различаться между собой. Поэтому спектральные линии излучения свободных атомов, возникающие при переходе электронов между энергетическими уровнями с различными n, будут иметь тонкую структуру, то есть расщепляться на несколько компонентов (рис.1.3), соответствующих различным l:
(В формуле (1.4) w – частота излучения, соответствующая переходу атомного электрона с энергетического уровня, характеризуемого квантовыми числами n и l, на уровень с меньшей энергией, который характеризуется числами n¢и l¢.) По просьбе Зоммерфельда, его соотечественник Фридрих Пашен проверил и подтвердил это следствие теории на примере спектральных линий гелия. Внимательно рассмотрев фотографию спектральной линии гелия, которая соответствует переходу с уровня n=4 на уровень n=3, он обнаружил, что она в действительности состоит из тринадцати тесно расположенных линий. Это удивительное совпадение в то время сравнивали с вычислениями Леверье и Адамса, которые «на кончике пера» открыли новую планету Солнечной системы – Нептун и предсказали, в какой точке неба астрономам следует ее искать. Следует отметить, что энергия электронов (1.3) в изолированных многоэлектронных атомах не зависит от значения магнитного квантового числа, то есть энергетический спектр свободных атомов вырожден по магнитному квантовому числу m. Это означает, что одному и тому же энергетическому подуровню отвечает, вообще говоря, несколько электронных орбиталей. Пространственная ориентация и число орбиталей на соответствующем энергетическом подуровне определяется магнитным квантовым числом m, которое характеризует величину проекции орбитального момента электрона на выделенную ось (например, на ось z):
Вырождение энергетического спектра атомов по магнитному квантовому числу снимается при помещении атомов в магнитное или электрическое поле. В этом случае за счет взаимодействия атомных электронов с полем отдельные подуровни, отвечающие определенному значению l, расщепляются на подуровни, соответствующие различным значениям m, вследствие чего спектральные линии излучающих атомов при помещении их во внешнее поле испытывают дополнительное расщепление на компоненты, отвечающие различным значениям магнитного квантового числа. Явление расщепление спектральных линий под действием внешнего магнитного поля было обнаружено еще в 1896 г. в опытах голландского физика Питера Зеемана. С тех пор оно известно как эффект Зеемана. Расщепление спектральных линий атомов во внешнем электрическом поле было открыто в 1913 г. немецким физиком Йохансом Штарком и называется эффектом Штарка. Магнитное квантовое число может принимать целочисленные значения от –l до +l, включая 0. Это значит, что число орбиталей, соответствующих энергетическому подуровню с определенным значением l равно 2l+1. Например, s-подуровню соответствует только одна орбиталь с m=0 (рис.1.2, а), р-подуровню – три р-орбитали с m = –1, 0 и +1 (рис.1.2, б), d-подуровню – пять орбиталей с m = –2, –1, 0, +1 и +2, и т. д. Число орбиталей, отвечающих главному квантовому числу п равно Таким образом, согласно выводам квантовомеханической теории многоэлектронные атомы имеют оболочечную структуру: электроны в таких атомах располагаются вблизи атомного ядра на оболочках, нумеруемых главным квантовым числом n, которые достаточно сильно отличаются друг от друга по размеру и энергии. Оболочки, в свою очередь, состоят из близких по энергии (рис.1.3, б) электронных орбиталей, которые нумеруются орбитальным квантовым числом l и магнитным числом m и отличаются друг от друга формой и ориентацией в пространстве. В спектроскопии различные оболочки принято называть большими буквами латинского алфавита: K (n=1), L (n=2), M (n=3), N (n=4) и т.д. Различные энергетические подуровни принято обозначать двумя числами – главным квантовым числом n и орбитальным числом l. При этом главное квантовое число обозначают соответствующими цифрами (n= 1, 2, 3, …), а орбитальный момент – малыми буквами латинского алфавита: s (l=0), p (l=1), d (l=2), f (l=3) и т.д. Например, уровень с квантовыми числами n=3, l=0 обозначают как 3s, а уровень с n=3, l=1 – как 3p. Число электронов, которые размещаются в атоме на энергетическом подуровне с определенными значениями главного и орбитального квантовых чисел, обозначают цифрой вверху, рядом с обозначением соответствующего подуровня. Например, если на 3p-подуровне размещаются 2 электрона, это записывают как 3p2. Заполнение электронных орбиталей происходит в порядке увеличения суммы (n+l) главного и орбитального квантовых чисел (правило Клечковского), то есть в порядке увеличения энергии электронов на этих орбиталях. Так, сумма (n+l) для электронов 3d-подуровня равна 3+2=5, а для электронов 4s-подуровня – 4+0=4. Поэтому электронами заполняется вначале 4s-орбиталь, а затем 3d-орбитали (калий, кальций, скандий, титан). Сумма (n+l) для электронов 4f-подуровня равна 4+3=7, что также больше суммы (n+l) для электронов 5s-, 5р- и 6s-подуровней. Поэтому первыми заполняются 5s-, 5р- и 6s-орбитали. При одинаковых значениях суммы (n+l) заполнение орбиталей происходит последовательно в направлении возрастания значения главного квантового числа п. Распределение электронов по орбиталям осуществляется в соответствии с открытым в 1924 г. принципом запрета Паули, согласно которому в атоме не может быть двух электронов с одинаковыми значениями главного, орбитального, магнитного и спинового квантового числа. Спиновоеквантовое число можно условно трактовать как характеристику вращения электрона вокруг собственной оси. Спиновым квантовым числом s называется проекция Sz собственного момента количества движения электрона на избранное направление (например, на ось z), выраженная в единицах h:
Спиновое число имеет два значения: +1/2 и –1/2. Обычно их изображают в виде противоположно направленных стрелок: и ¯ соответственно. Согласно принципу Паули на одной орбитали, характеризуемой определенными значениями главного, орбитального и магнитного квантовых чисел, могут находиться лишь два электрона с антипараллельными спинами (с s = +1/2 и –1/2). Таким образом, в соответствии с принципом Паули максимальное число электронов на подуровне, характеризуемом определенным значением l, равно 2(2l+1). Общее число электронов, которые могут разместиться на энергетическом уровне, характеризуемом квантовым числом n, равно 2n2. Из этих формул следует, что на одной s-орбитали (l=0) может находиться не более двух электронов, на трех р-орбиталях (l=1) – не более шести, на пяти d-орбиталях (l=2) – не более 10, на семи f-орбиталях (l=3) – не более 14 электронов. При этом максимальное число электронов в K-оболочке равно 2, в L-оболочке – 8, в М-оболочке – 18 и т. д. Распределение электронов по орбиталям называется электронной конфигурацией атома (таблица 1.1). Орбитали с одинаковыми энергиями (вырожденные) заполняются в соответствии с правилом Хунда, согласно которому наименьшей энергией обладает электронная конфигурация атома с максимальным суммарным спином электронов. Объяснение этого эмпирического правила связано со специфическим обменным взаимодействием электронов, которое приводит к понижению энергии состояний с параллельными спинами максимально возможного (с учетом принципа Паули) числа электронов. Благодаря обменному взаимодействию три p-электрона, например, будут располагаться на p-подуровне так, чтобы их суммарный спин был равен +3/2 (
Таблица 1.1.* Электронные конфигурации некоторых атомов. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 , (1.1)
, (1.1)


 . (1.2)
. (1.2)
 , (1.3)
, (1.3)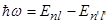 . (1.4)
. (1.4) . (1.5)
. (1.5) .
. . (1.6)
. (1.6)