|
|
САУ в электромеханике и электротехнологииА.М. Абакумов, В.И. Котенев САУ В ЭЛЕКТРОТЕХНОЛОГИИ Методическое пособие Самара Самарский государственный технический университет
А.М. Абакумов, В.И. Котенев
САУ В ЭЛЕКТРОТЕХНОЛОГИИ
Методическое пособие
Самара Самарский государственный технический университет Печатается по решению редакционно-издательского совета СамГТУ
УДК 62-52 (075) А13
Абакумов А.М. А 13САУ в электротехнологии и электромеханике:метод. пособие / А.М. Абакумов, В.И. Котенев. – Самара: Самар. гос. техн. ун-т, 2011. – 152 с.: ил.
ISBN 978-5-7964-1152-0
Рассматриваются принципы построения систем автоматического управления, вопросы анализа их работы в установившихся режимах, различные способы описания динамических характеристик звеньев систем, критерии устойчивости, методика расчета переходных процессов, методы синтеза и оценки чувствительности линейных систем управления. Приведены примеры составления математического описания, исследования устойчивости, построения переходных процессов, синтеза корректирующих устройств и оценки чувствительности систем управления. Предназначено для студентов, обучающихся по направлению 140600 «Электротехника, электромеханика и электротехнологии».
Рецензент – д-р техн. наук П.К. Кузнецов
УДК 62-52 (075) А 13
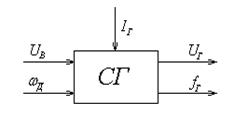
ISBN 978-5-7964-1152-0 © А.М. Абакумов, В.И. Котенев, 2011 © Самарский государственный ВВЕДЕНИЕ В современных электрических системах и системах электроснабжения (СЭС) управление режимами работы генерирующих устройств и многих энергоемких производственных установок (дуговые сталеплавильные печи, прокатные станы, индукционные нагревательные установки и др.) осуществляется с помощью автоматических систем. Статические и динамические свойства этих систем в значительной мере определяют протекание электромагнитных и электромеханических переходных процессов в СЭС и ее устойчивость [1]. Особое влияние на режим работы СЭС оказывают мощные синхронные двигатели, оснащенные системами автоматического регулирования возбуждения [2]. При рациональных алгоритмах регулирования такие системы позволяют эффективно управлять показателями качества электроэнергии в узлах нагрузки электрических систем. В связи с этим при изучении электромеханических и электромагнитных переходных процессов возникают задачи исследования статических и динамических характеристик различных систем управления, а также анализа устойчивости сложных динамических систем, к числу которых относятся электрические системы и СЭС. Методы решения указанных задач, а также общие принципы построения различных систем автоматического управления базируются на основных положениях теории автоматического регулирования и управления. 1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ 1.1. Понятие об управлении и регулировании. В теории автоматического управления и регулирования [3-6] различные технологические процессы, промышленные установки и машины, элементы энергетических систем и так далее рассматривают как объекты управления (ОУ). В качестве ОУ возьмем, например, синхронный генератор СГ (рис. 1.1). Состояние ОУ можно характеризовать его выходными переменными (величинами, координатами).
Рис. 1.1
Целью управления является обеспечение требуемого изменения некоторых выходных переменных объекта или поддержание их на постоянном уровне. Эти переменные называют управляемыми или регулируемыми. Выбор управляемой переменной (или переменных) зависит от конкретных условий решаемой технической задачи. Для синхронного генератора регулируемыми величинами могут быть частота Требуемое изменение регулируемых величин осуществляется с помощью регулирующих (управляющих) воздействий на ОУ. Для синхронного генератора такими воздействиями могут быть скорость вращения приводного двигателя В отличие от регулирующих воздействий, которые можно изменять целенаправленно, на ОУ действуют также возмущающие воздействия, вызывающие нежелательные изменения регулируемых величин. Основным возмущающим воздействием для синхронного генератора является изменение нагрузки – тока генератора В качестве еще одного примера ОУ рассмотрим узел нагрузки СЭС (рис. 1.2, а). Предположим, что асинхронные двигатели М1, М2 потребляют активную
Рис. 1.2
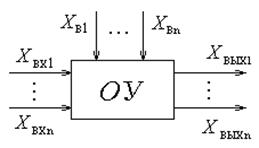
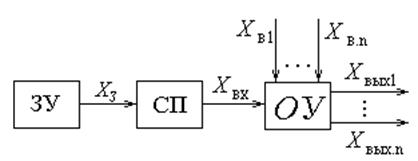
В общем случае ОУ на функциональной схеме изображается прямоугольником (рис. 1.3) с входящими управляющими
Рис. 1.3 При ручном и полуавтоматическом управлении требуемое изменение регулирующих воздействий на ОУ создается при участии человека. В случае автоматического управления формирование регулирующих воздействий на объект осуществляется с помощью автоматического управляющего устройства (регулятора), которое совместно с ОУ образует систему автоматического управления (САУ). В зависимости от требуемого характера изменения во времени регулируемой величины Системы стабилизации предназначены для поддержания постоянного значения регулируемой величины. Задающее воздействие в таких системах Системы программного управления предназначены для изменения управляемой величины по заранее известному закону (программе). С помощью таких систем может, например, осуществляться программное изменение реактивной мощности синхронного двигателя или конденсаторных батарей в зависимости от времени суток, движение по определенной траектории режущего инструмента металлообрабатывающего станка и др. В следящих системах задающее воздействие, поступающее на систему, изменяется по заранее неизвестному закону. Такая система так же, как и система программного управления, должна обеспечить следование (слежение) выходной, управляемой переменной за задающим воздействием, так чтобы поддерживалось равенство Кроме рассмотренного деления САУ дополнительно классифицируются по следующим основным признакам: 1) по виду уравнений, описывающих процессы управления, – на линейные и нелинейные; 2) по характеру передаваемых сигналов – на непрерывные и дискретные (импульсные и цифровые); 3) по характеру процессов управления – на детерминированные, в которых элементы взаимодействуют точно предвиденным образом, и вероятностные, имеющие случайные параметры или содержащие случайные процессы. Далее рассматриваются непрерывные детерминированные системы. При проектировании САУ в зависимости от предъявляемых технических требований используют различные принципы (методы) управления. Основные из них – управление по разомкнутому циклу, управление по разомкнутому циклу со связью по возмущению (или просто управление по возмущению), управление по отклонению, комбинированное управление. 1.2. Управление по разомкнутому циклу Примером системы, реализующей этот принцип, может служить система управления напряжением
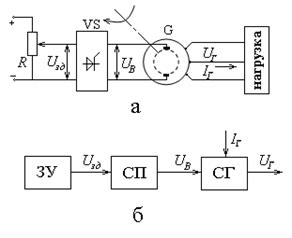
Рис. 1.4 Для пояснения принципа работы систем удобно использовать функциональные схемы, на которых элементы, выполняющие определенные функции, изображаются в виде прямоугольников (рис. 1.4, б). В рассматриваемой системе тиристорный возбудитель выполняет функцию силового преобразователя (СП), а потенциометр При постоянном значении задающего воздействия и действии возмущений, например при изменении нагрузки, напряжение генератора может значительно отклоняться от заданного, следовательно, система не обеспечивает стабилизацию регулируемой величины. Функциональная схема разомкнутой системы для общего случая показана на рис. 1.5. Она состоит из ОУ, силового преобразователя СП и задающего устройства ЗУ.
Рис. 1.5
Действие возмущений Принцип управления по разомкнутому циклу не позволяет добиться точного слежения выходной переменной за изменяющимся задающим воздействием. Изменение выходной переменной вследствие инерционности элементов системы может значительно отставать от изменения задающего воздействия. В связи с этим при создании САУ используют другие принципы управления. 1.3. Принцип управления по возмущению Система, построенная по этому принципу, состоит из следующих основных элементов (рис. 1.6): ОУ, регулятора и датчика возмущающего воздействия. Такая система является разомкнутой системой со связью по возмущению
Рис. 1.6
В системе (см. рис. 1.6) к ОУ приложено несколько возмущающих воздействий Выходной сигнал датчика
Складывается, если увеличение В зависимости от величины сигнала В качестве примера рассмотрим систему стабилизации напряжения синхронного генератора (рис. 1.7). Она содержит датчик ДВ основного возмущения – изменения тока нагрузки. Датчик состоит из трансформатора тока ТТ и выпрямительного моста VM. Напряжение
Рис. 1.7
Функциональная схема рассматриваемой системы приведена на рис. 1.7, б. Как видно по функциональной схеме, выход системы не связан со входом, т.е. система является разомкнутой. Управление по возмущению, так же как и управление по разомкнутому циклу, не позволяет обеспечить высокой точности слежения выходной величины за изменяющейся входной. 1.4. Принцип управления по отклонению Основными звеньями системы автоматического управления, построенной по отклонению, являются (рис. 1.8) объект управления, регулятор и датчик регулируемой величины. В САУ по отклонению измеренное значение действительного выходного сигнала
– поступает на вход регулятора. В зависимости от величины сигнала ошибки
Рис. 1.8 Такая САУ является системой с отрицательной обратной связью, потому что измеренное значение выходного сигнала Системы с ООС являются замкнутыми, а без ООС – разомкнутыми. Погрешность регулирования замкнутых САУ намного меньше погрешности разомкнутых систем, поэтому применение замкнутых систем как более сложных и дорогих целесообразно в тех случаях, когда разомкнутые системы не обеспечивают требуемой точности регулирования. При управлении напряжением синхронного генератора этот принцип может быть реализован с помощью схемы, представленной на рис. 1.9, а. Здесь используется датчик регулируемой величины, состоящий из трансформатора напряжения TV и выпрямительного моста VM. Напряжение датчика
В этой схеме любое отклонение регулируемой величины от заданного значения приводит к изменению сигнала датчика и сигнала ошибки, при этом напряжение возбуждении генератора Функциональная схема, изображенная на рис. 1.9, б, наглядно показывает, что система управления по отклонению является замкнутой: в ней выходная величина, измеренная датчиком (Д), в виде сигнала обратной связи
Рис. 1.9 В качестве еще одного примера управления по отклонению рассмотрим систему стабилизации внутреннего угла Θ синхронного двигателя М. Такие системы [2] используют для улучшения режима работы двигателя при переменной нагрузке. На обмотку возбуждения двигателя в этой схеме (рис. 1.10) поступает напряжение
Рис. 1.10 Угловая скорость Внутренний угол Θ характеризует взаимное положение векторов
где т – число фаз;
Рис. 1.11 Для некоторого значения Рассмотрим работу схемы по рис. 1.10. При возрастании угла Θ переменные будут изменяться следующим образом:
Расходящийся процесс свидетельствует о неустойчивости системы. Исследование устойчивости является одной из важнейших задач теории управления.
1.5. Комбинированный принцип управления В системе, построенной по комбинированному принципу управления (рис. 1.14), имеются канал связи по одному из возмущающих воздействий, например по воздействию
Рис. 1.14 Возмущающее воздействие измеряется датчиком ДВ1, а выходная величина Вопросы для самопроверки 1. Какие переменные можно рассматривать в качестве регулируемой величины управляющего и возмущающего воздействий для двигателя постоянного тока независимого возбуждения, генератора постоянного тока? 2. Укажите достоинства и недостатки каждого из рассмотренных принципов управления. 3. Что понимается под ООС? Почему системы с ООС называют замкнутыми? 2. СТАТИКА СИСТЕМ Статика – установившийся режим работы, когда сигналы в системе не изменяются в функции времени. Для упрощения исследования систем их разбивают на отдельные звенья, обладающие направленностью действия. Такие звенья передают воздействие только со входа на выход и не оказывают влияния на состояние предыдущего звена. Основными задачами исследования статики являются выявление факторов, от которых зависит статическая точность системы, и изучение статических характеристик звеньев и систем [3-5], [8]. 2.1. Коэффициент передачи звена. Свойства звена в установившемся режиме описываются уравнением статики
Рис. 2.1
График, изображающий функцию
Здесь коэффициент передачи звена
Если переменные В случае нелинейной характеристики (см. рис. 2.2) последнюю можно на достаточно малых участках приближенно заменить отрезками прямых (линеаризовать) и ввести понятие коэффициента передачи для отклонений:
Использование этого понятия упрощает аналитическое исследование системы. Линеаризация характеристик может быть выполнена двумя методами. При линеаризации по секущей (см. рис. 2.2, а) выбирают интервал (А, В), в пределах которого изменяются переменные, и заменяют действительную характеристику на этом интервале секущей АВ. Коэффициент передачи рассчитывают по выражению (2.2), определив
Рис 2.2
При линеаризации по касательной участок исходной характеристики (см. рис. 2.2, б) заменяют касательной, проведенной к рабочей точке А. Учитывая, что
Выражение (2.3) служит для аналитического определения коэффициента Таким образом, для нелинейной характеристики коэффициент передачи
Его значение зависит от выбранной точки линеаризации. Пример 2.1. Линеаризовать функцию Из формулы (2.4)
Размерность
В общем случае выходная переменная звена может быть нелинейной функцией нескольких входных величин:
Для линеаризации такой функции используют степенной ряд Тейлора. Пренебрегая членами второго порядка (и более), выражение для отклонений можно записать в виде
Значения частных производных здесь представляют собой коэффициенты передачи по соответствующим переменным, т. е. выражение (2.5) является обобщением формулы (2.4). Очевидно, что линеаризация применима только к непрерывно дифференцируемым нелинейностям. Звенья, не удовлетворяющие этим требованиям, например с релейными характеристиками, называются существенно нелинейными. Пример 2.2. Линеаризовать выражение (1.2) для угловой характеристики синхронного двигателя, считая переменными В соответствии с уравнением (2.5) получим
где Значения
Отрицательный знак коэффициента 2.2. Определение коэффициентов передачи Звенья САУ могут быть включены одним из следующих способов: последовательно, параллельно, в виде участка (системы) с ООС, в виде участка (системы) с положительной обратной связью (ПОС). Получим выражения для общего коэффициента передачи звеньев, включенных указанными способами. Примечание. Здесь и далее для упрощения записей опускается знак приращения Δ, при этом не следует забывать, что в случае нелинейных звеньев рассматриваются приращения переменных. При последовательном включении (рис. 2.3, а) выходная величина первого звена
Рис. 2.3
Общий коэффициент передачи
В случае параллельного включения (рис. 2.3, б) на входы звеньев поступает сигнал
Общий коэффициент передачи
В этом выражении коэффициенты передачи суммируются с учетом их знака. Для случая системы (участка) с ООС свернутая схема приведена на рис. 2.3, в, где
а сигналы ошибки и обратной связи определяются соотношениями
Подставляя их в выражение для
откуда общий коэффициент передачи
Если систему с ООС разомкнуть, например, по цепи обратной связи, что условно показано на рис. 2.3, в, то звенья с коэффициентами 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
и (или) величина генерируемого напряжения 
.
и напряжение возбуждения 
.
.
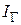и реактивную 
мощности, величины которых могут изменяться. Синхронные двигатели М3, М4, работающие в режиме перевозбуждения, являются источниками реактивной мощности 
. Ставится задача стабилизации реактивной мощности 
, потребляемой от энергосистемы. Тогда для рассматриваемого ОУ (рис. 1.2, б) регулируемой величиной будет мощность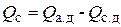 
, возмущающим воздействием –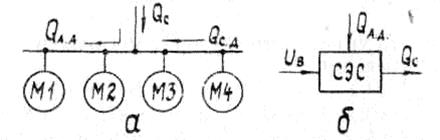 
; возмущающими 
воздействиями и выходящими из него регулируемыми переменными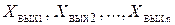 
.
САУ делят на системы стабилизации, программного управления и следящие.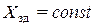
. Часто требуется, например, обеспечить стабилизацию скорости вращения двигателя, напряжения и частоты синхронного генератора и др. Системы стабилизации называют также системами автоматического регулирования.
. Примером следящей системы может служить САУ, с помощью которой ось антенны радиолокационной станции сопровождает цель, движущуюся по заранее неизвестному закону, и др.
синхронного генератора G (рис. 1.4, а). На обмотку возбуждения генератора поступает напряжение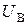 
(регулирующее воздействие) от тиристорного возбудителя VS. Его величину можно изменять с помощью задающего воздействия 
, снимаемого с потенциометра 
.
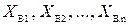в такой системе ничем не компенсируется, что приводит к большим погрешностям в регулировании выходных координат 
.
, а не замкнутой системой, так как в ней отсутствует связь выхода ОУ с входом регулятора.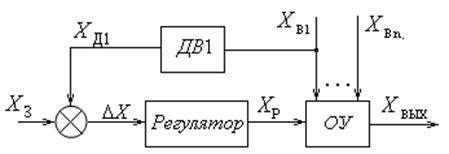
, пропорциональный 
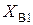, складывается или вычитается из сигнала задания:
.
, и вычитается, если увеличение 
регулятор вырабатывает управляющее воздействие 
на ОУ, которое стремится уменьшить отклонение выходной величины от заданного значения. При действии остальных возмущений 
система работает как разомкнутая.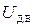
с выхода датчика складывается с задающим, и на вход VS поступает сигнал 
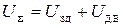. Если генератор работает на холостом ходу, 
. При возрастании нагрузки напряжения 
увеличиваются и на обмотку возбуждения генератора подается большее напряжение. Благодаря этому предотвращается снижение напряжения 
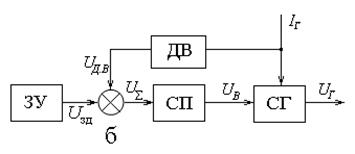
вычитается из входного сигнала 
, а разностный сигнал – сигнал ошибки системы
регулятор вырабатывает управляющее воздействие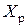 
, которое препятствует отклонению действительного выходного сигнала от его желаемого значения.
вычитается из входного сигнала.
=Uос, пропорциональное регулируемой величине 
, сравнивается с задающим, и на вход тиристорного преобразователя VS поступает сигнал ошибки
. (1.1)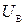
изменяется так, чтобы вернуть напряжение генератора к заданному значению. Например, при снижении напряжения 
переменные будут изменяться следующим образом: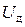 
– уменьшится; 
– в соответствии с выражением (1.1) увеличится; 
поступает на вход, где сравнивается с задающим воздействием. Отрицательный знак связи условно указан зачернением соответствующего сектора узла сравнения. Для большей наглядности рядом, в скобках, могут показываться и знаки сигналов.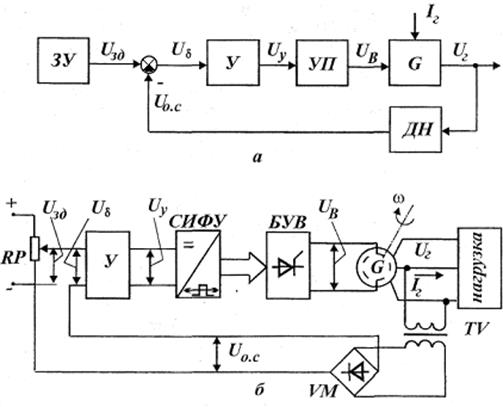
, где 
– сигнал датчика (ДУ) внутреннего угла Θ.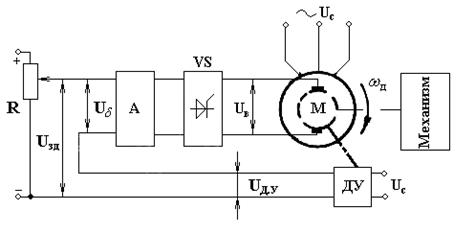
синхронного двигателя в установившихся режимах равна угловой скорости поля статора. В частности, для двигателя с одной парой полюсов (рис. 1.11, а) 
вектора напряжения сети 
. В переходных режимах, например при изменении нагрузки, 
, связанный с положением ротора, «отстает» или «догоняет» вектор 
.
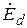и может рассматриваться в качестве выходной переменной синхронного двигателя. В установившихся режимах момент сопротивления 
, создаваемый механизмом, уравновешивается электромагнитным моментом 
, который для неявнополюсного двигателя описывается выражением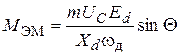
, (1.2)
– индуктивное сопротивление двигателя по продольной оси.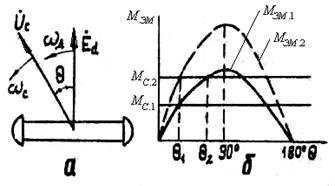
угол Θ определяется по угловой характеристике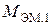 
и равен Θ1 (рис. 1.11, б). При увеличении момента до значения 
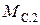угол Θ принимает значение Θ2. Дальнейшее возрастание момента 
за счет увеличения напряжения возбуждения двигателя. В этом случае, в соответствии с выражением (1.2), двигатель будет переходить на новую, более высоко расположенную характеристику 
, а угол Θ может остаться неизменным.
– уменьшится; 
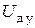– уменьшится; 
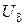– увеличится; 
В системах с ООС удается также повысить точность слежения выходной величины за изменяющимся входным воздействием. Например, при ступенчатом изменении задающего воздействия (рис. 1.12, а) в системе управления напряжением генератора (см. рис. 1.9) на вход тиристорного возбудителя в первый момент времени поступает повышенное напряжение 
. Благодаря этому происходит интенсивное нарастание выходной величины 
снижается, и напряжение 
, чем в случае разомкнутой системы (кривая 2 на рис. 1.12).
В замкнутых системах, однако, могут возникать и расходящиеся переходные процессы. В случае положительной обратной связи выходная величина 
может отклоняться от заданного значения по апериодическому закону (кривая 1 на рис. 1.13). Расходящийся процесс может возникать и в системе с ООС. Например, если в схеме на рис. 1.13 тиристорный возбудитель будет воздействовать на синхронный генератор излишне энергично, то регулируемая величина будет каждый раз приближаться к заданному значению 
со все большим ускорением, и процесс будет расходящимся, колебательным (кривая 2 на рис. 1.13).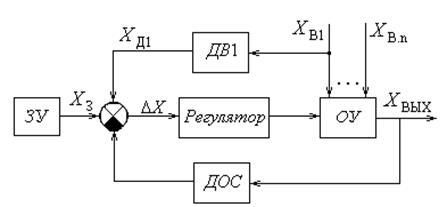
, ..., 
система работает как система с ООС.
, где 
– соответственно выходная и входная переменные.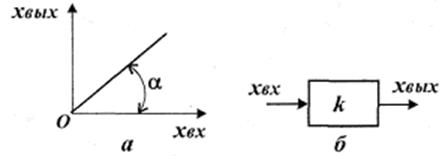
(рис. 2.1, а; 2.2), называется статической характеристикой. В случае линейной характеристики (см. рис. 2.1) уравнение статики имеет вид
. (2.1)
представляет собой отношение выходной переменной к входной:
.
имеют одинаковую физическую природу, 
. (2.2)
и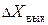 
из графика. Этот метод удобно использовать, когда характеристика задана графически.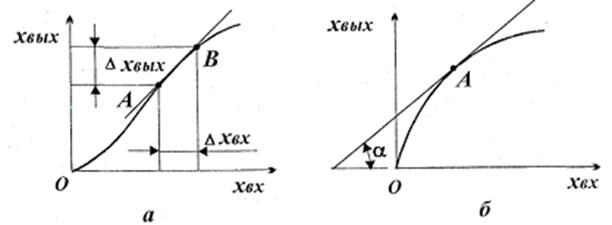
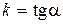, а тангенс угла наклона касательной к кривой определяется через производную, можно записать
. (2.3)
. (2.4)
, считая переменной 
. Значение 
.
.
.
.
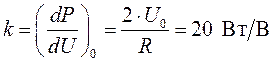. (2.5)
.
(2.6)
и 
– коэффициенты передачи двигателя по приращению угла и приращению эдс.
и 
принимаются в зависимости от выбранной точки линеаризации, например это могут быть номинальные значения эдс и угла. Из последнего выражения можно найти также коэффициент передачи двигателя по изменению эдс при постоянном моменте на валу. Принимая 
, получим
.
свидетельствует о том, что положительному приращению (увеличению) эдс 
.
является входной для второго звена, в свою очередь, выходная величина второго звена поступает на вход третьего звена, и т. д. Учитывая это, можно записать следующее:
.
. (2.7)
, а их выходные величины суммируются: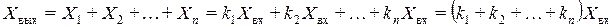
.
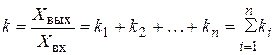. (2.8)
и 
– коэффициенты передачи прямой цепи и цепи обратной связи. Если исходная схема содержит параллельно и последовательно включенные звенья, ее можно свести к указанному виду, используя выражения (2.7), (2.8). Выходной сигнал системы с ООС
,
.
, получим
,
. (2.9)