
|
|
Точечно-векторное аффинное пространствоЛинейные пространства. Определение Опр.Множество X называется линейным пространством над полем K, если: 1. Существует закон, который позволяет каждым двум элементам
2. Существует закон, который позволяет каждому элементу
3. Законы, введенные в X, удовлетворяют следующим аксиомам: 1. 2. 3. 4. 5. 6. 7. 8. Элементы пространства X обычно называют векторами, элемент Из определения непосредственно вытекают следующие элементарные свойства линейного пространства: 1. В любом линейном пространстве существует единственный 2. В любом линейном пространстве для каждого элемента существует единственный противоположный элемент. 3. Для всякого вектора 4. Для всякого вектора
4.1. Сист координат в пространстве Если в пространстве Vn зафиксировать некоторую точку O, то в силу свойств 1 и 2 между всеми остальными точками и векторами устанавливается взаимно однозначное соответствие. Вектор Опр.Системой координат в пространстве Vn, называется совокупность фиксированной точки O и некоторого базиса Координатами вектора Координатами точки А в данной системе ко- Всякие два базиса пространства Vn Если даны две системы координат O,
Подпространства линейного пространства Опр.Всякое подмножество L линейного пространства X, заданного над полем K, которое, в свою очередь, является линейным пространством, называется линейным подпространством. Для того, чтобы подмножество L линейного пространства X являлось линейным подпространством, необходимо и достаточно, чтобы 1. 2. Опр.Пусть M – подмножество векторов пространства X. Совокупность всех линейных комбинаций векторов из М называется линейной оболочной L(M) векторов М. Всякая линейная оболочка является линейным подпространством. Размерность линейной оболочки L(M), натянутой на векторы множества M, равна числу линейно независимых векторов данного множества. Опр.Суммой L двух подпространств L1 и L2 одного и того же пространства X называется множество векторов вида Сумма линейных подпространств Опр.Пересечением L линейных подпространств L1 и L2 называется совокупность векторов, принадлежащих одновременно L1 и L2. Обозначается Пересечение линейных подпространств Опр.Прямой суммой L двух подпространств L1 и L2 называется сумма этих подпространств при условии, что их пересечение состоит лишь из нулевого вектора. Обозначается Размерности суммы и пересечения подпространств L1 и L2 связаны между собой следующим соотношением Точечно-векторное аффинное пространство Опр.Пусть некоторое множество Множество 1. Каждая пара точек А1 и A2, заданных в определенном порядке, определяет единственный вектор 2. Для каждой точки А1, и каждого вектора 3. Если Пространство 4.2.Прямая и плоскость в Vn Опр.Пусть в аффинном пространстве Vn заданы собственное подпространство L и фиксированный вектор называется плоскостью в Vn. Размерностью плоскости X называется размерность соответствующего подпространства Одномерная плоскость пространства Vn называется прямой линией. Плоскость размерности Две плоскости называются совпадающими, если они состоят из одних и тех же точек (векторов) пространства; в противном случае они называются несовпадающими. Множество точек n-мерного пространства, принадлежащих как плоскости X1, так и плоскости X2, называется их пересечением, а сами плоскости X1 и X2 пересекающимися, если Две несовпадающие плоскости Из определения плоскости следует, что всякая плоскость является линейным многообразием. Всякая k-мерная плоскость
где
ранга n-k, где В частности, всякая прямая задается либо системой линейных уравнений ранга
где
Наконец, в координатной форме можно записать каноническое уравнение прямой
где Всякая гиперплоскость задается одним линейным уравнением

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
,  поставить в соответствие элемент
поставить в соответствие элемент  , называемый суммой и обозначаемый
, называемый суммой и обозначаемый
 и каждому числу
и каждому числу  поставить в соответствие элемент
поставить в соответствие элемент  , называемый «произведением элемента
, называемый «произведением элемента  на число
на число  » и обозначаемый
» и обозначаемый
 ,
, 
 ,
, 




 :
: 









 , где 1 — единица поля K.
, где 1 — единица поля K. — нулевым вектором, элемент
— нулевым вектором, элемент  — противоположным (обратным) к вектору
— противоположным (обратным) к вектору  .
. .
.




 называется радиус-вектором точки А относительно т O.
называется радиус-вектором точки А относительно т O. в Vn.
в Vn. .
. относительно базиса.
относительно базиса. и
и  связаны между собой формулами перехода
связаны между собой формулами перехода  где вектор-столбцы матриц перехода
где вектор-столбцы матриц перехода  и
и  состоят из координат векторов
состоят из координат векторов  и
и  соответственно в базисах
соответственно в базисах  и
и  .
. и
и  ,
,  , то координаты любой точки
, то координаты любой точки  и
и  относительно этих систем координат связаны соотношениями
относительно этих систем координат связаны соотношениями ,
,  где
где 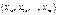 – координаты точки
– координаты точки  в
в  – матрица перехода.
– матрица перехода.

 и
и 

 , где
, где  и
и  . Обозначается
. Обозначается  .
. сама является линейным подпространством.
сама является линейным подпространством.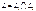 .
. .
.
 состоит из элементов двух типов, которые будем называть «точками» и «векторами». Пусть при этом множество векторов образует n-мерное линейное пространство, а множество точек не пусто.
состоит из элементов двух типов, которые будем называть «точками» и «векторами». Пусть при этом множество векторов образует n-мерное линейное пространство, а множество точек не пусто. называется точечно-векторным аффинным пространством, если:
называется точечно-векторным аффинным пространством, если: .
. существует единственная точка A2, такая, что
существует единственная точка A2, такая, что  .
. и
и  , то
, то  .
. называется n-мерным, если n-мерно соответствующее линейное пространство.
называется n-мерным, если n-мерно соответствующее линейное пространство. .Множество
.Множество 
 .
. называется гиперплоскостью.
называется гиперплоскостью. .
.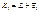 и
и  , полученные сдвигом одного и того же подпространства L, называются параллельными.
, полученные сдвигом одного и того же подпространства L, называются параллельными. может быть задана либо параметрическим уравнением
может быть задана либо параметрическим уравнением ,
, — базис в L,
— базис в L,  — произвольные числа, либо как линейное многообразие системой линейных неоднородных уравнений
— произвольные числа, либо как линейное многообразие системой линейных неоднородных уравнений
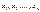 — координаты вектора
— координаты вектора  .
. , либо параметрическим уравнением
, либо параметрическим уравнением
 — направляющий вектор прямой, λ — параметр. Если
— направляющий вектор прямой, λ — параметр. Если  и
и  — радиус-векторы двух точек прямой, то можно записать уравнение прямой, проходящей через две данные точки
— радиус-векторы двух точек прямой, то можно записать уравнение прямой, проходящей через две данные точки ,
, 
 ,
, — координаты точки
— координаты точки  ,
,  — координаты некоторой фиксированной точки прямой;
— координаты некоторой фиксированной точки прямой;  -координаты направляющего вектора
-координаты направляющего вектора 