
|
|
Основные свойства определенного интеграла
3. Если отрезок интегрирования
4.
где 5. Определенный интеграл от алгебраической суммы конечного числа функций, интегрируемых на отрезке
Величина определенного интеграла от функции
Формула (23) называется формулой Ньютона-Лейбница. Из этой формулы следует, что для вычисления определенного интеграла достаточно найти какую-либо из первообразных для подынтегральной функции и из ее значения, соответствующего верхнему пределу интегрирования, вычесть значение, соответствующее нижнему пределу. Пример 9. Вычислить определенный интеграл Решение. Первообразной для функции
Основные методы вычисления определенных интегралов Метод разложения (непосредственного интегрирования) Этот метод основан на использовании свойств определенного интеграла, знании формул простейших неопределенных интегралов и применении формулы Ньютона-Лейбница.
Пример 10. Вычислить определенный интеграл
Решение. Воспользуемся свойствами (3) и (4) определенных интегралов:
Первообразные для подынтегральных функций найдем с помощью формул простейших определенных интегралов. Далее, используя формулу Ньютона-Лейбница, получим
Метод замены переменной (метод подстановки)
Этот метод основан на замене переменной интегрирования в определенном интеграле с целью свести его вычисление к вычислению такого определенного интеграла, который может быть вычислен методом разложения. Пример 11. Вычислить интеграл
Решение. Введем новую переменную При замене переменной интегрирования в определенном интеграле необходимо одновременно заменить пределы интегрирования на соответствующие . Имеем: при
Замечание. Если при замене переменной в неопределенном интеграле мы от новой переменной
Метод интегрирования по частям
Этот метод основан на использовании следующей формулы интегрирования по частям:
где Пример 12. Вычислить определенный интеграл Решение. Данный интеграл не может быть вычислен непосредственно ни методом разложения, ни методом замены переменной. Положим
Некоторые приложения определенного интеграла Вычисление площадей плоских фигур
Применение определенного интеграла для вычисления площадей плоских фигур основано на геометрическом смысле определенного интеграла: площадь S криволинейной трапеции, ограниченной графиком функции y = f (x), осью абсцисс и прямыми линиями x = a и x = b , численно равна определенному интегралу от этой функции на отрезке
Если плоская фигура ограничена прямыми x=a , x=b (a<b) и кривыми y=f1(x) , y=f2(x) , причем f1(x)<f2(x) (a<x<b) , то ее площадь вычисляется по формуле:
В частном случае, когда плоская фигура ограничена снизу осью OX, формула (25) упрощается:
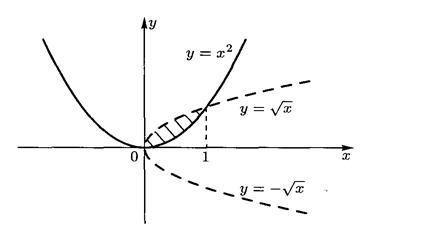
Пример13. Вычислить площадь фигуры, ограниченной кривыми (рис.5)
Рис.5 Решение. Найдем точки пересечения кривых :
Работа переменной силы Сравнивая формулу (4) с формулой (5) для определенного интеграла, приходим к выводу, что работа переменной силы f(x), действующей на материальную точку при перемещении ее из точки x=a в точку x=b, численно равна определенному интегралу от этой силы на отрезке
Пример 14. Найти величину работы, которую необходимо совершить для растяжения пружины от положения равновесия на величину l=0,1 м, если коэффициент упругости пружины k=200 Н/м. Решение. В соответствии с законом Гука для растяжения пружины на величину x необходимо приложить силу f(x)=kx. Подставляя это выражение в (27) , получим зависимость работы А приложенной силы от растяжения l пружины:
Подставив в эту формулу численные значения, окончательно получим:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
.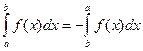 .
.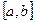 разделен на конечное число n частичных отрезков
разделен на конечное число n частичных отрезков  , то определенный интеграл от функции
, то определенный интеграл от функции 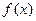 на отрезке
на отрезке  .
.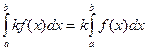 ,
,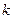 - постоянный множитель.
- постоянный множитель.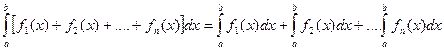 .
. , (23)
, (23)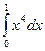 .
.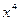 (имеющей наиболее простой вид), является
(имеющей наиболее простой вид), является 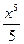 . Поэтому в соответствии с формулой Ньютона-Лейбница имеем
. Поэтому в соответствии с формулой Ньютона-Лейбница имеем  .
.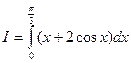 .
.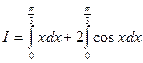 .
.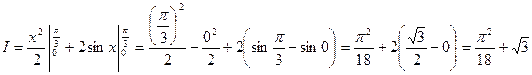 .
.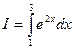 .
.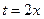 ; Тогда
; Тогда 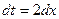 , откуда
, откуда 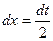 .
.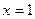
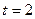 , при
, при 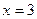
 . Отсюда следует, что новым нижним пределом интегрирования будет значение 2, а новым верхним – значение 6. Таким образом
. Отсюда следует, что новым нижним пределом интегрирования будет значение 2, а новым верхним – значение 6. Таким образом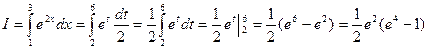 .
.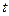 возвращались к первоначальной переменной
возвращались к первоначальной переменной 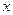 , то при замене переменной в определенном интеграле в этом нет необходимости.
, то при замене переменной в определенном интеграле в этом нет необходимости.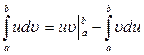 , (24)
, (24) и
и  - непрерывно дифференцируемые функции на отрезке
- непрерывно дифференцируемые функции на отрезке 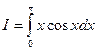 .
.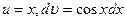 . Найдем отсюда
. Найдем отсюда 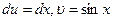 . Тогда
. Тогда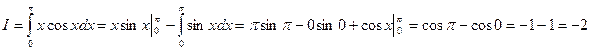
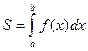 .
.

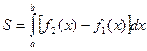 , (25)
, (25)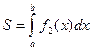 , (26)
, (26)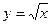 и
и 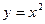 .
.
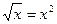 , следовательно
, следовательно 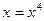 . Отсюда
. Отсюда 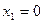 ,
, 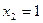 и по формуле (25) имеем
и по формуле (25) имеем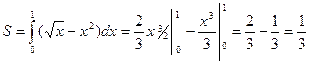

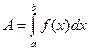 , (27)
, (27)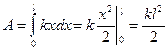 .
.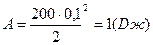 .
.